Playing with a fan cart

In order to illustrate what happens when a constant force is applied I have brought a fan cart. This is a little cart on wheels with a fan that can blow and propel it forward or backward depending on which way the fan is turned. When I turn on the fan, I believe that everyone would agree that the fan produces a force on the cart. When I hold the cart the force is balanced by my arm, the net force is zero and it stays put. When I put the cart on a table and let go, the fan's force is no longer balanced and that unbalanced force accelerates the cart forward. I wish to let the cart go on a track in various situations and show you what the graphs of velocity vs..... time look like in those situations. You will also see how the force shows up in each case.

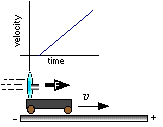
First I hold the cart on the track with the fan on. The cart is pointing towards the positive side of our number line and the fan is pointing backward so the force pushes in the positive direction. I'll start the time clock, then let go of the cart. The cart starts from zero velocity a little after the t=0 point (because I waited a bit before I let it go). Then the velocity increases with a constant positive slope. The slope of this graph is the acceleration and it is positive. The net force is proportional to the acceleration, so this graph implies a positive net force on the cart.

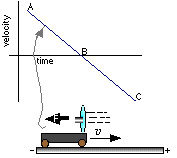
Next I turn the cart around and give it a big shove towards the positive end of the track. After I let go the fan's force pushes in the negative direction, and the graph shows negative acceleration. When the cart comes to a stop and I catch it, the velocity graph stops at point B. But if the cart is allowed to keep going, it will turn around and keep accelerating in the negative direction.

Notice that even though the velocity is instantaneously zero at point B on the graph, the slope never changes. Thus the acceleration remains constant throughout the run, even when the velocity passes though zero. The idea that there can be a nonzero acceleration when the velocity is zero seems odd, but it follows from the way we define velocity and acceleration.

Thus negative acceleration can occur both

when the cart is going in the positive direction and is slowing down,
when it is going in the negative direction and is speeding up and
when the velocity is momentarily zero while the cart is changing from moving in the positive direction motion to the negative direction.

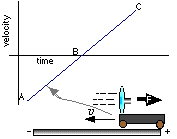
Finally think about the graph when I go to the other end of the track, and shove the cart towards the negative direction. When the fan is pointed in the direction of the shove, the force is positive and the cart slows down. The acceleration is positive because the negative velocity decreases. As the cart passes through point B, even though the velocity is momentarily zero, the positive acceleration never ceases as it turns around and accelerates towards the positive end of the track.

Thus positive acceleration can occur

when the cart is going in the positive direction and is speeding up,
when it is going in the negative direction and is slowing down and
when the velocity is momentarily zero while the cart is changing from moving in the negative direction to the positive direction.

Force and Mass

The equation F = ma is one of the most important in physics. Yet we have so far not explained how to get a quantitative operational definition of either mass or force. Somehow, from this one expression, we are going to figure out an operational measure of both of those undefined quantities. This probably seems akin to the miracle of the loaves and fishes!

It is necessary to establish a standard mass. I doesn't matter when, how, or where it is done, but that's the first step. If you were stranded on a desert island and wanted to start from scratch, you could just pick up any convenient rock, set it aside and use that as a standard mass. There is a lump of metal in a building near Paris that has served for many years as the standard kilogram. [Nowadays we have more elegant ways of defining the standard, but let's not get into that.] We can determine the inertial mass of any other object by comparing the acceleration of it to the acceleration of the standard mass under the same conditions. Here's how.

Op Def of Mass

Figure out some way to apply a reproducible force on objects and eliminate or cancel out any other forces acting on it such as friction (get rid of it) or gravity (cancel it out).
Apply the force to the standard kilogram mass, m_s and measure its acceleration a_s.
Apply the same force to the unknown mass, m_u and measure its acceleration a_u.
The ratio of the inertial masses is the same as the ratio of their accelerations. That comes from F=m_s a_s = m_ua_u because the force is the same. Thus

m_u/m_s = a_s/a_u

m_u = m_s (a_s/a_u)
This way one can compare masses by just measuring accelerations with a clock and a meter stick without knowing the value of the force used. The assumption is that the same force is acting on both masses. One can check that the force doesn't change with time by going back and trying it on the standard mass again and checking that the acceleration hasn't changed from the first time.

Op Def of Force

To get a numerical value for forces one must use the following procedure:

Apply the force to be measured to a mass of known value (as determined above). Again one must eliminate the effects of other forces if they are present.
Measure the acceleration of the mass.
Calculate the value of the force as as F = m a. The units of force will be kilogram€meter/second-squared. This unit is composed of the three fundamental SI units and is called a newton for short. It is abbreviated N. (Note that units named after people start with a small letter when written out in full, but use a capital letter when abbreviated.) How big is a newton? What does it feel like? Pick up a small apple and your hand will feel a newton. It's about the weight of a 100 g mass on earth.

It's difficult to define both force and mass absolutely rigorously while not making it seem very obscure to the beginning student. The descriptions here are, I believe, better than those usually found in introductory physics textbooks and agrees with the treatments in some of the books I like such as the PSSC texts, Eric Rogers' Physics for the Inquiring Mind and Arnold Arons' books. You can also read the discussions in March's Physics for Poets.

Question The country of Nomassia refuses to establish a standard for mass. Instead it has enshrined a standard spring in its Bureau of Standards. When extended an exact length indicated on its case, then it exerts the Nomassian standard force called a "nomass". How would the operational definitions of force and mass outlined above have to be changed in Nomassia? What would be the unit of mass be expressed in fundamental units of meters, seconds and nomasses?

Inertial Mass and Gravitational Mass

The method of determining mass by pulling it with a spring and measuring acceleration seems very inconvenient. It is more convenient to compare two masses by putting them on a balance. If an object with unknown mass on one side exactly balances a standard kilogram mass on the other side, then the object has a mass of one kilogram. But you might not see the logical connection between balancing two masses in earth's gravity and comparing how hard it is to accelerate them with an applied force. You would be right! One property of all objects is that the earth exerts a force on them downward. This forces seems to be larger the more material there is. This is what the balance compares and it has no obvious connection with the measure of how difficult it is to get them moving. The casual observation that both properties seem to grow larger with the amount of material is no guarantee that they grow larger in the same proportion for all materials.

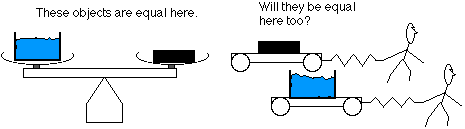
To see this consider a balance with a lump of iron on one side and a plastic bottle of water on the other. Iron and water are very different materials. We know that water is made of light elements oxygen and hydrogen and the bottle has some carbon in it which is also light. Iron is a relatively heavy element, very different from water. If I pour enough water in the bottle so that the force of earth's gravity on it is the same as the force of gravity on the iron bar, then they balance. Can you be absolutely certain that these two quantities of water and iron will also have equal resistance to being accelerated by an applied force (i.e, the same inertia)? You really have to try it and see. When it has been tried it has always been found that when the force of gravity is equal, then the inertia is equal. This has been checked to a very high degree of accuracy!

Because these two properties are logically different, we should call them by different words. The property that resists acceleration is called inertial mass. The property of an object that causes earth to exert a force on it is called gravitational mass. It is only from experiments that we can say that the number we get for one property can be also used for the other property. Is this a coincidence?

In order to find a system where the equivalence of these two properties follows logically we really have to envision strange things. Einstein's theory of general relativity is an attempt to "explain" this equivalence. In this theory all bodies travel between two points along the path of least distance: a geodesic. The way gravity comes about is that a mass causes nearby space and time to curve. Then an object travelling through curved space along the shortest path will be appear to be attracted to the other mass which is causing the space to be curved. Of course each of the masses causes space around it to curve. In this way the amount of gravitational attraction between two objects is proportional to the amount inertial mass in both objects. This gets ahead of our subject because we haven't even learned Newton's theory of gravitation, let alone Einstein's.

What's the use of all this?

The relationship between force, mass and acceleration is the first fact learned by observing the physical world which we have encountered in this course. Let's look at one practical application which we can appreciate right now. We all know how it's dangerous for us to come to a sudden, unexpected stop when we are going at high speeds. For this reason we are encouraged to wear helmets when riding bicycles and motorcycles and airbags are recommended for car safety. All of these devices work by increasing the amount of time it takes to come to a stop from your cruising velocity. You can illustrate the effectiveness of increasing the time between full speed and full stop by hurling an egg into a bed sheet held up to catch the egg. If the sheet is held loosely so that it can absorb the shock of the egg then it's almost impossible to break the egg when it's caught in the sheet. On the other hand, an egg colliding with a hard object tries to stop in a much shorter time period. It breaks.

We can understand this by estimating the force exerted on the egg by the object with which it collides. The average acceleration is given by the difference in the velocities at full speed and at zero speed divided by the time it takes to stop. The corresponding average force is got by multiplying the average acceleration by the mass of the egg. Let's do an example.

Let's assume that when a 30-gram egg hits a brick wall it stops in the time between two TV pictures: 1/30th second. If Michael hurls the egg at a speed of 10 m/s then the force will be

F = m a = 0.03 kg x 10 m/s /(1 /30) s = .03 x 30 x 10 = 9 N.

That's almost the force of a 1 kg mass on earth. That may be enough to break the shell, especially if it's spread over a small area. The force on a contact area 1 mm by 1 mm would be about 90 times atmospheric pressure. (Pressure is the force divided by the area it is applied to.) Spread out the stopping time over half a second and then the force would be reduced by 15 times. Another effect of the sheet would be to increase the contact area so that the pressure would be further reduced.

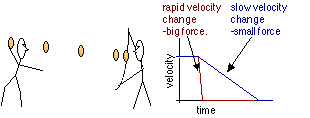
Stay healthy, stop slowly!