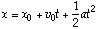Acceleration
We cannot even approximation real motion by intervals of constant velocity.
No real object can instantaneously change from one velocity to another.
The change in velocity takes place during an interval of time.
For example in the interval of time from t1to t2,
delta-t, the velocity may change from v1 to v2,
delta-v.
The ratio delta-v/delta-t is called the acceleration. If the acceleration is not
constant and the time interval is finite then this ratio is the average acceleration.
Acceleration is the slope of the velocity-time graph. Recall that velocity
was the slope of the position-time graph. If acceleration is not constant then
the instantaneous acceleration at any time is the slope of the tangent line on the
velocity-time graph at that time.
For example, the Power Wheels started from a dead stop and reached a velocity
of 1 m/s in 2 s. The average acceleration is (1 m/s)/(2 s) = 0.5 m/s/s.
The car reached a higher value of instantaneous acceleration during the 2 s interval which
you might try to estimate by drawing a tangent line. We usually write
0.5 m/s2. Writing the units of acceleration as m/s/s is acceptable and
is not ambiguous if one applies the usual rule of evaluating operators from left to right.
So far the concept of acceleration is probably pretty familiar to you
because of its common usage to describe speeding up. The term is used
in physics in a much broader sense. For example if v1
is larger than v2 then we would have a negative
acceleration. This happens, for example, when one is travelling in the
positive direction and is slowing down. Colloquially, we describe this
with the term deceleration, but technically, the term acceleration applies
to this case as well. Furthermore, travelling in the negative direction and
slowing down gives a positive acceleration and travelling in the negative
direction and speeding up is negative acceleration. The sign of the
acceleration is not necessarily the same as the velocity's. This means that
the acceleration's direction is not always the same as the direction of
the veolcity. When we start talking about two and three dimensional motion
this fact becomes even more important. To reiterate, in common usage,
acceleration means going faster in the forward direction. In physics it means
the ratio of velocity change and time interval during which that velocity
change occurred. That's not always the same thing.
Relations for constant acceleration
The graphical way of deriving displacements from a velocity-time graph
is completely general. No matter what the motion is, as long as it can
be represented graphically, we can estimate the displacement during
any time interval by estimating the area under the curve.
Formulas for constant acceleration can be derived and are useful even though
constant acceleration rarely occurs exactly. Falling objects, if they are
heavy and dense enough, may approach constant acceleration fairly closely. In
other cases, such as the braking of a train, assumming constant acceleration may
be a useful first approximation to the actual braking motion. Thus the
formulae for constant acceleration are usually a staple of first year physics
courses. (They also form a convenient topic for problems early on in the course.)
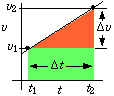
First sketch the velocity-time graph for constant positive acceleration and
positive velocity. The displacement between any two times is got by
figuring out the area under the curve. This area is a quadrilateral which
is not rectangular unless the acceleration is zero. We can figure out the
area by first getting the area of the rectangle and adding the area of the triangle.
(Remember that the area of the triangle is 1/2 base x height.)
Area of quadrilateral = Area of rectangle + Area of triangle
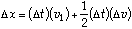
recall that
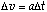 which comes directly from the definition of acceleration.
which comes directly from the definition of acceleration.
Thus

This is the equation of a parabola, and if you look at the graph of
position vs time for constant acceleration you will see that a parabola is
a reasonable curve to fit the graph.
Even though we used a picure of positive acceleration and positive velocity
to derive this equation, you should verify that it is general and applies
in cases of negative acceleration or negative velocity or both.
Problem: Draw velocity-time graph for negative acceleration, positive velocity
and verify that the equation applies. Repeat for the other two combinations
of signs of acceleration and velocity.
This equation is so important and popular among physics teachers that it is usally
called one of the "Kinematic equations". Sometimes slightly different
notation may be used. For example, the one I remember goes like this:
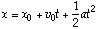
In this case t is used for delta-t and delta-x =x - x0.
Remember that this equation applies only for constant acceleration.
Another kinetmatic equation applies for constant velocity, zero
acceleration is
delta-x = v (delta-t)
As I said, many traditional early problems in your physics courses involve
manipulating these "kinematic equations" and you may wish to memorize them.
If you forget the equation relating displacement to constant acceleration, just
redraw the little graph and figure out the areas as we did above.
Return to Main Page
©1999,2000, N. Alberding, Simon Fraser University.

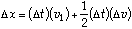
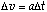 which comes directly from the definition of acceleration.
which comes directly from the definition of acceleration.