We cannot even approximate real motion by intervals of constant velocity. No real object can instantaneously change from one velocity to another. The change in velocity takes place during an interval of time. For example in the interval of time from t1to t2, Δt, the velocity may change from v1 to v2, Δv. The ratio Δv/Δt is called acceleration. If the acceleration is not constant and the time interval is finite then this ratio is the average acceleration. Acceleration is the slope of the velocity-time graph. Recall that velocity was the slope of the position-time graph. If acceleration is not constant then the instantaneous acceleration at any time is the slope of the tangent line on the velocity-time graph at that time.For example, the Power Wheels started from a dead stop and reached a velocity of 1 m/s in 2 s. The average acceleration is (1 m/s)/(2 s) = 0.5 m/s/s. The car reached a higher value of instantaneous acceleration during the 2 s interval which you might try to estimate by drawing a tangent line. We usually write 0.5 m/s2. Writing the units of acceleration as m/s/s is acceptable and is not ambiguous if one applies the usual rule of evaluating operators from left to right.
So far the concept of acceleration is probably pretty familiar to you because of its common usage to describe speeding up. The term is used in physics in a much broader sense. For example if v1 is larger than v2 then we would have a negative acceleration. This happens, for example, when one is travelling in the positive direction and is slowing down. Colloquially, we describe this with the term deceleration, but technically, the term acceleration applies to this case as well. Furthermore, travelling in the negative direction and slowing down gives a positive acceleration and travelling in the negative direction and speeding up is negative acceleration. The sign of the acceleration is not necessarily the same as the velocity's. This means that the acceleration's direction is not always the same as the direction of the veolcity. When we start talking about two and three dimensional motion this fact becomes even more important. To repeat, in common usage, acceleration means going faster in the forward direction. In physics it means the ratio of velocity change and time interval during which that velocity change occurred. That's not always the same thing.
Playing with a fan cart
In order to illustrate what happens when a constant force is applied I have brought a fan cart. This is a little cart on wheels with a fan that can blow and propel it forward or backward depending on which way the fan is turned. When I turn on the fan, I believe that everyone would agree that the fan produces a force on the cart. When I hold the cart the force is balanced by my arm, the net force is zero and it stays put. When I put the cart on a table and let go, the fan's force is no longer balanced and that unbalanced force accelerates the cart forward. I wish to let the cart go on a track in various situations and show you what the graphs of velocity vs. time look like in those situations. You will also see how the force shows up in each case.First I hold the cart on the track with the fan on. The cart is pointing towards the positive side of our number line and the fan is pointing backward so the force pushes in the positive direction. I'll start the time clock, then let go of the cart. The cart starts from zero velocity a little after the t=0 point (because I waited a bit before I let it go). Then the velocity increases with a constant positive slope. The slope of this graph is the acceleration and it is positive. The net force is proportional to the acceleration, so this graph implies a positive net force on the cart.
Next I turn the cart around and give it a big shove towards the positive end of the track. After I let go the fan's force pushes in the negative direction, and the graph shows negative acceleration. When the cart comes to a stop and I catch it, the velocity graph stops at point B. But if the cart is allowed to keep going, it will turn around and keep accelerating in the negative direction.Notice that even though the velocity is instantaneously zero at point B on the graph, the slope never changes. Thus the acceleration remains constant throughout the run, even when the velocity passes though zero. The idea that there can be a nonzero acceleration when the velocity is zero seems odd, but it follows from the way we define velocity and acceleration.
Thus negative acceleration can occur both
- when the cart is going in the positive direction and is slowing down,
- when it is going in the negative direction and is speeding up and
- when the velocity is momentarily zero while the cart is changing from moving in the positive direction motion to the negative direction.
Finally think about the graph when I go to the other end of the track, and shove the cart towards the negative direction. When the fan is pointed in the direction of the shove, the force is positive and the cart slows down. The acceleration is positive because the negative velocity decreases. As the cart passes through point B, even though the velocity is momentarily zero, the positive acceleration never ceases as it turns around and accelerates towards the positive end of the track.Thus positive acceleration can occur
- when the cart is going in the positive direction and is speeding up,
- when it is going in the negative direction and is slowing down and
- when the velocity is momentarily zero while the cart is changing from moving in the negative direction to the positive direction.
Relations for constant acceleration
The graphical way of deriving displacements from a velocity-time graph is completely general. No matter what the motion is, as long as it can be represented graphically, we can estimate the displacement during any time interval by estimating the area under the curve.
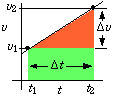
Formulas for constant acceleration can be derived and are useful even though constant acceleration rarely occurs exactly. Falling objects, if they are heavy and dense enough, may approach constant acceleration fairly closely. In other cases, such as the braking of a train, assumming constant acceleration may be a useful first approximation to the actual braking motion. Thus the formulae for constant acceleration are usually a staple of first year physics courses. (They also form a convenient topic for problems early on in the course.)First sketch the velocity-time graph for constant positive acceleration and positive velocity. The displacement between any two times is got by figuring out the area under the curve. This area is a quadrilateral which is not rectangular unless the acceleration is zero. We can figure out the area by first getting the area of the rectangle and adding the area of the triangle. (Remember that the area of the triangle is 1/2 base × height.)
Area of quadrilateral = Area of rectangle + Area of triangle
$$ \Delta x = (\Delta t) (v_1) + \frac{1}{2}\Delta t \Delta v$$
recall that $\Delta v = a \Delta t$ which comes directly from the definition of acceleration.
Thus
$$\Delta x = v_1 \Delta t + \frac{1}{2}a (\Delta t)^2$$
This is the equation of a parabola, and if you look at the graph of position vs time for constant acceleration you will see that a parabola is a reasonable curve to fit the graph.
Even though we used a picure of positive acceleration and positive velocity to derive this equation, you should verify that it is general and applies in cases of negative acceleration or negative velocity or both.Problem: Draw velocity-time graph for negative acceleration, positive velocity and verify that the equation applies. Repeat for the other two combinations of signs of acceleration and velocity.This equation is so important and popular among physics teachers that it is usally called one of the "Kinematic equations". Sometimes slightly different notation may be used. For example, the one I remember goes like this:
$$x= x_0 + v_0t + \frac{1}{2}at^2$$
In this case $t$ is used for $\Delta t$ and $x_0 = x - \Delta x$.
Remember that this equation applies only for constant acceleration.Another kinetmatic equation is useful when you know inital and final velocities, but not the acceleration.
Going back to the original analysis of constant acceleration $$ \Delta x = (\Delta t) (v_1) + \frac{1}{2}\Delta t \Delta v$$ we can substitute $$\Delta v = v_2 - v_1$$ $$ \Delta x = (\Delta t) (v_1) + \frac{1}{2}\Delta t\left(v_2 - v_1 \right)$$ Simplifying $$ \Delta x = \Delta t\frac{v_1 + v_2}{2} $$ This is saying that during a period of constant acceleration, the distance travelled by an object is the same as if it travelled at a velocity exactly half-way between the initial and final velocities. In other words, the average velocity is the average of the initial and final velocities. This is only true if the acceleration is constant. It's very useful for many kinematics problems.
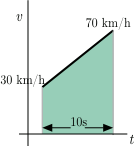
Example: A car accelerates constantly from 30 km/h to 70 km/h during 10 s. How far does the car go during this time?Solution: Draw a graph:
We want the shaded area, which represents displacement. Use $$\Delta x = \Delta t\frac{v_1 + v_2}{2} $$ $$\Delta x = 10 \rm s\frac{30 {\rm km/h} + 70 {\rm km/h}}{2}$$ $$\Delta x =( 10 \rm s) ( 50 {\rm km/h) (1h/3600s)} = 0.138 \rm km$$
Example: A car is backing to a stop at a constant rate of slowing. It goes 50 m and stops in 7 s. How fast was it going when it started slowing down?
Solution: Draw a graph:
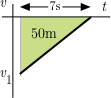
We know the shaded area is −50 m. The stopping time is 7s and forms the base of the triangle. We also know that the final speed, $v_2$ is 0.Solve: $$\Delta x = \Delta t\frac{v_1 + 0}{2} $$ for $v_1$. $$v_1 = 2\frac{\Delta x}{\Delta t} = 2\frac{-50 \rm m}{7 \rm s} = -14.3 {\rm m/s}$$
As I said, many traditional early problems in your physics courses involve manipulating these "kinematic equations" and you may wish to memorize them. If you forget the equation relating displacement to constant acceleration, just redraw the little graph and figure out the areas as we did above.
Return to Main Page
©1999, 2000, 2009, 2010 N. Alberding, Simon Fraser University.