Train Problem

A speeding express train travelling at 70 miles/h approaches a slow freight train travelling 40 miles/h The freight train is 1 mile ahead of the express and moving the same direction. The engineer of the express applies the brakes when it is 1 mile behind the freight train. It takes 2 miles to stop stop the express from 70 miles/h. Will they collide? Assume that the rate of braking is constant and that the freight train doesn’t change its speed.

Step 1. Sketch velocity vs time graph and position vs time graphs showing what is known:
the speeds of the two trains and the braking distance. We can choose $t=0$ when the brakes are first applied.

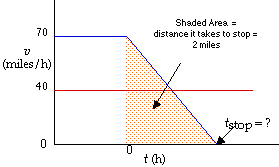
figure 1: velocity vs time graph


figure 2: position vs time graph showing two possible outcomes

Step 2. Figure out the time it takes the express to stop completely. We know it takes 2 miles, but how much time does it take?

$$\frac{1}{2}v_{\rm express}t_{\rm stop} = d_{\rm stop}$$ solve for $t_{\rm stop}$ $$ t_{\rm stop} = 2 \frac{d_{\rm stop}}{v_{\rm express}}= 2 \frac{2 {\rm ~miles}}{70{\rm ~miles/h}}= \frac{2}{35} {\rm~hour}$$ That's less than 4 minutes.

Step 3. Find the time to slow from 70 mph to 40 mph assuming constant deceleration.
The upper triangle in figure 3 is similar to the large triangle used in step 2 because the horizontal line at 40 mph is parallel to the time axis.

figure 3: Use v vs t graph to find the time to slow to 40 miles/h and how far the express catches up.

$$\frac{t_{40}}{t_{\rm stop}} = \frac{30}{70}$$ $$t_{40} = \frac{30}{70}t_{\rm stop}$$ $$t_{40} = \frac{30}{70}\times\frac{2}{35}{\rm ~hour}= \frac{6}{245}{\rm ~hour}$$

step 4. The area of small upper triangle in figure 3 represents how much farther the express train travels than the freight train travels until their speeds are the same. In other words, the area is how much the express train catches up with the freight train while its trying to slow down to its speed. If this distance is greater than the mile lead that the freight train has, then there will be a crash.


catch-up distance = $\frac{1}{2} \left( \frac{6}{245} \rm ~h \right){(30 \rm~miles/h)} = \frac{90}{245} {\rm ~mile}= \frac{18}{49} {\rm ~mile}$

In other words, the distance between the trains decreases by less than 1/2 mile so all should be ok.

Alternate method using the “Kinematic Equations”

step 1: Same as above:

step 2: Same as above

Step 3: Find acceleration:

$$a = \frac{-70 {\rm ~miles/h}}{2/35 {\rm ~h}} = -1225 {\rm ~miles/h}^2
$$
(That works out to about −0.55 m/s²)

Step 4:

How long does it take to reach 40 miles/h at this rate of acceleration (or decelration)?

Use

$$v_f = v_i + at$$ Solve for $t$: $$t = \frac{v_f-v_i}{a} = \frac{40 {\rm ~miles/h} - 70 {\rm ~miles/h}}{-1225 {\rm ~miles/h}^2}$$ $$t=\frac{-30}{-1225}{\rm ~h}=\frac{6}{245}{\rm ~h}$$

Step 5:
Find where the freight train is when the express reaches 40 miles/h. Assume $x_{\rm i(freight)}$ = 1 mile when the brakes were applied at $t=0$.

Kinematic Eq 1 gives $$x_{\rm freight}(t) = x_{\rm i(freight)} + vt$$ $$x_{\rm freight}\left(t=\frac{6}{245}\rm h\right) = 1 {\rm~mile} + (40{\rm~miles/h}) \left(\frac{6}{245}\rm h\right) = 1\frac{240}{245}{\rm~miles}$$ That's almost 2 miles.


Find where the express train is when it achieves a speed of 40 miles/h:

Kinematic Equation 2: $$x_{\rm express}(t) = x_{\rm i(express)} + v_{\rm i(express)}t + \frac{1}{2}at^2$$ $$x_{\rm express}\left(t=\frac{6}{245}\rm h\right) = 0 {\rm~mile} + (70{\rm~miles/h}) \left(\frac{6}{245}\rm h\right) +\frac{1}{2}(-1225 {\rm~miles/h}^2)(\frac{6}{245}\rm h)^2$$
$$ = 0 + \frac{420}{245}{\rm~ miles} - \frac{1}{2}\left(\frac{5\times7\times5\times7\times36}{245\times5\times7\times7}\right)$$
$$= \frac{420}{245} - \frac{90}{245}{\rm miles} = \frac{330}{245}{\rm miles} = 1 \frac{85}{245} {\rm miles}$$ (Almost 1.5 miles)
The freight train is still ahead! The distance between the trains is

$1 \frac{240}{245} - 1 \frac{85}{245} = \frac{155}{245}$ miles.

When the brakes were first applied they were $\frac{245}{245}$ miles apart, so the separation decreased by $\frac{90}{245}$ miles as we found in the previous method.