Example 5.2: Using the INQUAD= Option

The NLP Procedure

Example 5.2: Using the INQUAD= Option

This example illustrates the INQUAD= option for specifying a quadratic programming problem:

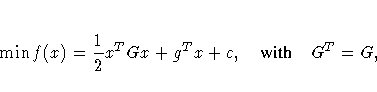
$\min f(x) = {1 \over 2} x^T G x + g^T x + c, {with} G^T = G ,$

Suppose that c=-100, G = diag(.4,4) and that $2 \leq x_1 \leq 50$ , $-50 \leq x_2 \leq 50$ ,and $10 \leq 10x_1 - x_2$ .

You specify the constant c and the Hessian G in the data set QUAD1. Notice that the _TYPE_ variable contains the keywords that identify how the procedure should interpret the observations.

data quad1;
   input _type_ $ _name_ $ x1 x2;
   datalines;
    const   .   -100  -100
    quad   x1    0.4     0
    quad   x2      0     4
;

You specify the QUAD1 data set with the INQUAD= option. Notice that the names of the variables in the QUAD1 data set and the _NAME_ variable match the names of the parameters in the PARMS statement.

proc nlp inquad=quad1 all;
   min ;
   parms x1 x2 = -1;
   bounds  2 <= x1 <= 50,
         -50 <= x2 <= 50;
   lincon 10 <= 10 * x1 - x2;
run;

Alternatively, you can use a sparse format for specifying the c and G matrices eliminating the zeros. You use the special variables _ROW_, _COL_, and _VALUE_ to give the nonzero row and column names and value.

data quad2;
   input _type_ $ _row_ $ _col_ $ _value_;
   datalines;
    const  .      .    -100
    quad   x1    x1     0.4
    quad   x2    x2       4
   ;

You can also include the constraints in the QUAD data set. Notice how the _TYPE_ variable contains keywords that identify how the procedure is to interpret the values in each observation.

data quad3;
   input _type_ $ _name_ $ x1   x2   _rhs_;
   datalines;
         const      .     -100  -100   .
         quad       x1    0.02     0   .
         quad       x2    0.00     2   .
         parms      .       -1    -1   .
         lowerbd    .        2   -50   .
         upperbd    .       50    50   .
         ge         .       10    -1  10

proc nlp inquad=quad3;
   min ;
   parms x1 x2;
run;

Chapter Contents
Previous
Next
Top