Line-Search Methods

The NLMIXED Procedure

Line-Search Methods

In each iteration k, the (dual) quasi-Newton, conjugate gradient, and Newton-Raphson minimization techniques use iterative line-search algorithms that try to optimize a linear, quadratic, or cubic approximation of f along a feasible descent search direction s^(k)

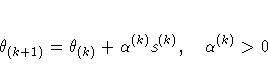
$\theta_{(k+1)} = \theta_{(k)} + \alpha^{(k)} s^{(k)} , \alpha^{(k)} \gt 0$

by computing an approximately optimal scalar $\alpha^{(k)}$ .

Therefore, a line-search algorithm is an iterative process that optimizes a nonlinear function $f(\alpha)$ of one parameter ( $\alpha$ ) within each iteration k of the optimization technique. Since the outside iteration process is based only on the approximation of the objective function, the inside iteration of the line-search algorithm does not have to be perfect. Usually, it is satisfactory that the choice of $\alpha$ significantly reduces (in a minimization) the objective function. Criteria often used for termination of line-search algorithms are the Goldstein conditions (refer to Fletcher 1987).

You can select various line-search algorithms by specifying the LIS= option. The line-search method LIS=2 seems to be superior when function evaluation consumes significantly less computation time than gradient evaluation. Therefore, LIS=2 is the default method for Newton-Raphson, (dual) quasi-Newton, and conjugate gradient optimizations.

You can modify the line-search methods LIS=2 and LIS=3 to be exact line searches by using the LSPRECISION= option and specifying the $\sigma$ parameter described in Fletcher (1987). The line-search methods LIS=1, LIS=2, and LIS=3 satisfy the left-hand side and right-hand side Goldstein conditions (refer to Fletcher 1987). When derivatives are available, the line-search methods LIS=6, LIS=7, and LIS=8 try to satisfy the right-hand side Goldstein condition; if derivatives are not available, these line-search algorithms use only function calls.

Chapter Contents
Previous
Next
Top