Newton-Raphson Method

The PHREG Procedure

Newton-Raphson Method

Let $L({{\beta}})$ be one of the likelihood functions described in the previous subsections. Let $l({{\beta}})={\rm log} L({{\beta}})$ . Finding ${\beta}$ such that $L({{\beta}})$ is maximized is equivalent to finding the solution $\hat{{\beta}}$ to the likelihood equations

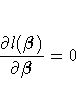
$\frac{\partial l({\beta}) }{\partial {\beta}} = 0$

With $\hat{{\beta}}^0 = 0$ as the initial solution, the iterative scheme is expressed as

$\hat{{\beta}}^{j+1}=\hat{{\beta}}^j-[ \frac { \partial^2 l ( \hat{{\beta}}^j ) ... ...{\beta}}^2} ]^{-1} \frac { \partial l ( \hat{{\beta}}^j) }{ \partial{{\beta}} }$

The term after the minus sign is the Newton-Raphson step. If the likelihood function evaluated at $\hat{{\beta}}^{j+1}$ is less than that evaluated at $\hat{{\beta}}^j$ ,then $\hat{{\beta}}^{j+1}$ is recomputed using half the step size. The iterative scheme continues until convergence is obtained, that is, until $\hat{{\beta}}_{m+1}$ is sufficiently close to $\hat{{\beta}}_m$ . Then the maximum likelihood estimate of ${\beta}$ is $\hat{{\beta}}=\hat{{\beta}}_{m+1}$ .

The estimated covariance matrix of $\hat{{\beta}}$ is given by

$\hat{V} ( \hat{{\beta}})=-[ \frac {\partial^2 l ( \hat{{\beta}}) }{ \partial {\beta}^2 } ] ^{-1}$

Chapter Contents
Previous
Next
Top