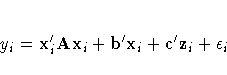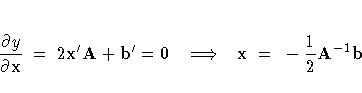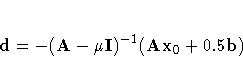Computational Method
Canonical Analysis
For each response variable, the model can be written in the form
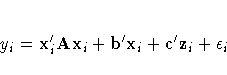
where
- yi
- is the ith observation of the response variable.
- xi
- = (xi1, xi2, ... , xik)'
are the k factor variables for the ith observation.
- zi
- = (zi1, zi2, ... , ziL)'
are the L covariates, including the intercept term.
- A
- is the k ×k symmetrized matrix of quadratic parameters,
with diagonal elements equal to the coefficients of the pure
quadratic terms in the model and off-diagonal elements equal
to half the coefficient of the corresponding cross product.
- b
- is the k ×1 vector of linear parameters.
- c
- is the L ×1 vector of covariate
parameters, one of which is the intercept.

- is the error associated with the ith observation.
Tests performed by PROC RSREG assume that errors are independently
and normally distributed with mean zero and variance
 .
.
The parameters in A, b, and
c are estimated by least squares.
To optimize y with respect to x,
take partial derivatives, set them to zero, and solve:
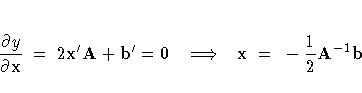
You can determine if the solution is a maximum or minimum
by looking at the eigenvalues of A:
| If the eigenvalues... | | then the solution is... |
| are all negative | | a maximum |
| are all positive | | a minimum |
| have mixed signs | | a saddle point |
| contain zeros | | in a flat area |
Ridge Analysis
The eigenvector for the largest eigenvalue gives
the direction of steepest ascent from the stationary
point, if positive, or steepest descent, if negative.
The eigenvectors corresponding to small or zero
eigenvalues point in directions of relative flatness.
The point on the optimum response ridge at a given
radius R from the ridge origin is found by optimizing
-
(x0 + d)'A(x0 + d) + b'(x0 + d)
over d satisfying d'd = R2,
where x0 is the k ×1 vector containing
the ridge origin and A and b are as
previously discussed.
By the method of Lagrange multipliers,
the optimal d has the form
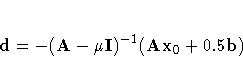
where I is the k ×k identity matrix and
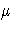 is chosen so that d'd = R2.
There may be several values of
is chosen so that d'd = R2.
There may be several values of 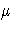 that
satisfy this constraint; the right one depends
on which sort of response ridge is of interest.
If you are searching for the ridge of maximum response, then
the appropriate
that
satisfy this constraint; the right one depends
on which sort of response ridge is of interest.
If you are searching for the ridge of maximum response, then
the appropriate 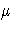 is the unique one that satisfies the
constraint and is greater than all the eigenvalues of A.
Similarly, the appropriate
is the unique one that satisfies the
constraint and is greater than all the eigenvalues of A.
Similarly, the appropriate 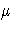 for the ridge
of minimum response satisfies the constraint and
is less than all the eigenvalues of A.
(Refer to Myers and Montgomery (1995) for details.)
for the ridge
of minimum response satisfies the constraint and
is less than all the eigenvalues of A.
(Refer to Myers and Montgomery (1995) for details.)
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.