When one WAVEFORM is displaced in space or time from another with the same period or a HARMONIC multiple of it, there is said to be a PHASE difference between them, usually expressed in degrees.
For instance, when a complex tone is subjected to FOURIER ANALYSIS, the resulting Fourier coefficients give the amplitudes and phase angles of the various harmonic components of the tone. On this basis one can determine what phase differences there are between the harmonics and the FUNDAMENTAL.
Constant phase differences are not normally detected by the ear, but this is not true for time-dependent spectra, (i.e. sounds which change timbrally in time) or sounds with slowly changing phase differences (see secondary BEATS, PHASING). The waveforms shown below are the result of combining the first and second harmonics with different phase angles between them. Although they look different, their perceived sound will be the same.
For a discussion of the importance of phase differences in localization, see BINAURAL HEARING. See also: CANCELLATION, INTERFERENCE, LAW OF SUPERPOSITION, PHASE-SHIFT.
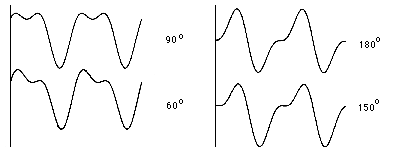
Four waveforms composed of a fundamental and second harmonic where the phase difference between these components is as listed at right. Although the shapes are different, these waves will generally sound alike.
home