
This article describes the physics and mathematics behind a class
of solutions to the Einstein field equations known as the
"warp-drive" metrics. These metrics have been studied (mainly just
for fun although they reveal some interesting properties of the
field equations) since 1994 and many of the references may be found
at the end of the article. This article is divided into two parts.
A non-mathematical part accessible to all (hopefully) which relies
heavily on analogies with well known systems and asks the reader to
believe some statements without proof. The second part is slightly more rigorous and mathematical. It requires some mathematical sophistication as well as some knowledge of General Relativity and Quantum Field Theory.
A. DeBenedictis
Part I Qualitative discussion.
The idea of traveling to distant stars and galaxies is, to many, quite appealing. Just hop on a rocket and go, right? Well, no, not really. First
of all, it would require an awful lot of fuel to accelerate the rocket to high velocities so that the trip could take place in a reasonable
amount of time for the astronaut. Here also lies the crux of another problem, namely, time dilation. You see, relativity tells us that if you
travel close to the speed of light on the ship and then come back to Earth, the time which passes on the ship is much less than that which has
elapsed on Earth. In other words, if the trip to a distant star and back takes a few years for the astronaut, many years have passed on Earth. When the astronauts get back, human society
may well have experienced thousands of years (or more). Heck, enough time may have passed for us to have evolved second heads if the astronauts travel at a high enough speeds and far enough distances. This curious effect is related (although it may not be obvious) to the fact that nothing with mass (like a rocket or astronaut) can be accelerated to the speed of light or beyond. The speed of light may seem fast to us but when considering traversing distances on a galactic scale, it is really quite slow (it takes light 100,000 years to cross our galaxy one way!)
Ok, so just putting in lots of fuel in a rocket and setting it off on its way is not such a useful way to explore the universe. Ironically, the very theory which forbids us to explore at
arbitrary velocity may also be the one which saves us. The argument I'm going to present is grossly simplified. However, the argument is essentially correct barring some minor musings into
things such as how the universe like a spring (it's not but the spring is a good analogy).
Consider an un-stretched spring as show in figure 1. This spring is going to represent space. That's right, the space you see around you and that you see when you look up at the night sky.
Why a spring? Well, General Relativity treats space (and time) as a dynamical quantity. That is, space can bend and stretch and shrink ( warp!) in different ways as time passes. Kind
of like a spring! Now, imagine that you live in the spring (you live in the universe after all). Since you live in the spring, you will feel the effects of this stretching and
bending. These effects have a fancy name. They are called gravity. Gravity is described by the theory of General Relativity. Saying that nothing in the universe can travel faster than the
speed of light is like saying that nothing in our spring can move faster than the speed of light relative to the spring , or more specifically, relative to certain disturbances of
the spring, which we shall now discuss. (This analogy is not quite correct but will suffice for our
purpose. What I am really trying to say is that nothing can travel faster than the speed of light but that this is a local phenomenon.)
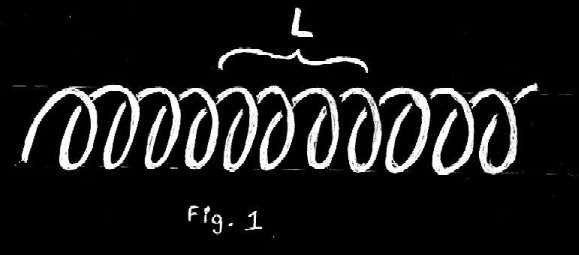
Now consider a section of spring of length L as shown in the diagram. Imagine that our spaceship is located at the center of this section. We know that the spaceship cannot move faster than
the speed of light in the spring. The question is then, is it possible to move a small disturbance within the spring faster than the speed of light? Also, if our spaceship is located in
this section of spring can it be arranged so that it moves along with the disturbance? (Remember that relativity forbids (well, this is not strictly speaking true but let us not
worry about that for now) anything in our spring to move faster than the speed of light
relative to the spring, but if a section of the spring is moving "faster" than the speed of light and we are moving slowly (eg. walking) within this section, the speed of light limit is
not violated.)
A Professor named Miguel Alcubierre demonstrated that the answer to the above questions turns out to be "yes" (actually the answer to the first question had been known for some time).
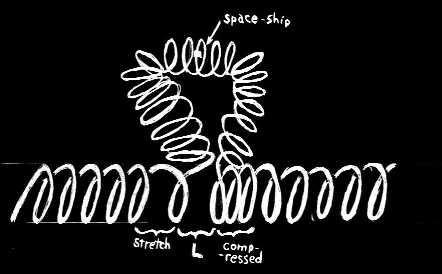
So the issue we now wish to address is "how do we do it?". I suspect you have seen a spring before and know how to stretch and compress one. What we wish to do is the following: Place your
ship somewhere in the section L of the spring, create a disturbance such that an uncompressed section of length L travels down the spring at an arbitrary speed, your ship will travel with
this disturbance. Figure 2 demonstrates this procedure. The ship position is indicated in the figure.
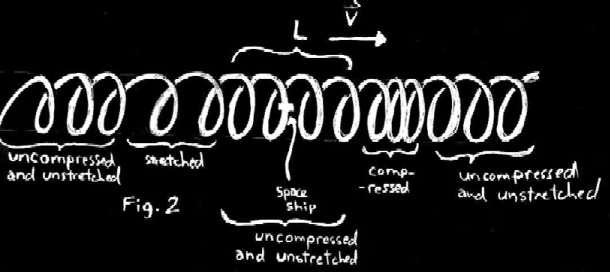
Ok, at this point you may be asking yourself (and rightly so) why isn't the ship moving faster than the speed of light? After all, it is only the disturbance that is moving at
arbitrary speed and not a section of the physical spring. Well, unfortunately the answer may not satisfy. The analogy with the spring is a bit artificial (you don't say?). Our space, or
specifically space-time, does not behave exactly like some solid object like a spring. However, the spring is a pretty good model as long as we are aware of its short-falls. In space-time
you can have a "piece of space-time" move within the greater whole. If the spring seems a bit hard to swallow, think instead of a "rigid plate" moving within a compressible (and extensible)
fluid. At this point it should also be stressed that the ship does not move at apparent super-luminal velocity by compressing the space in
front of it and traveling through this compressed space. The ship is never in the compressed region. It is in a region where there is no compression. The compression discussed
here
is simply a by-product of the type of metric chosen. It should be noted that one may keep the volume in all sections of the spring constant by also stretching and compressing the spring
sideways. This is the "volume preserving" warp
drive first studied by José Natário.
Why must the section L be uncompressed? Well, remember that stretching and shrinking and bending will be felt by the crew of the ship as gravitational effects. If you stretch the segment or
compress it too much the crew will be really uncomfortable (dead maybe... squished or exploded by gravitational forces). Notice from the diagram that to move the disturbance down the
spring we need to compress the spring in front of the ship and stretch the spring behind the ship. At these points then, there will be large gravitational effects but the crew members will
be safe as long as they stay away from these points. These points make up what is called the "warp bubble" (try to think in 3D instead of 1D... actually, this problem is 4D but let's not
worry about that 'til later.) So what do we have so far: The ship is inside the warp bubble and experiences almost no gravitational effects. The rest of the universe is outside the warp
bubble and it also doesn't feel the effects of the warp bubble. The warp bubble, along with the inside (the region of length L) and your ship move along the spring as fast as you want. Note
that nothing is moving faster than the speed of light relative to the spring (or more accurately, the spring disturbance.) Also, one very desirable
property of this construction is that, if
the crew members are moving around inside the warp bubble at much less than the speed of light, then there is no difference between the amount of time which passes inside the warp
bubble and outside the warp bubble (on Earth, for example)! No second head.
As you can imagine, it takes energy to form a warp bubble. Just like the energy associated with the Earth bends the space and, more importantly, dilates the time around it. So must the
ship's warp generating engines produce energy to warp the space around the ship (actually there's more to it than just energy but that's not important for our purposes). You may think that
an enormous amount of energy is required to generate a warp bubble which can encompass a spaceship. Actually, the problem is that it requires an extremely small amount of energy to power
the warp drive. Let me next explain this last statement.
In the everyday world, objects have positive mass and positive energy. Actually, by the formula E=mc2, energy and mass are basically the same thing. Well, to generate a warp
drive as described above, it take a fair amount of negative energy! Negative energy is difficult to describe. It is sufficient to say that on macroscopic scales (for example
something the size of an ant's foot or larger), negative energies (or negative masses) have not been observed. The negative energy such as that which is required to support the warp bubble
does have some ties with experiments, however. In quantum field theory one may place two conducting parallel plates close together in a vacuum and the region between the plates will have a
(albeit small) negative energy density. You see, in quantum field theory the vacuum is not nothing. It's a whole bunch of stuff (fields) whose quanta are constantly popping in and out of
existence. The vacuum is a very complicated object and many books have been dedicated to the vacuum. In fact, many researchers dedicate a lot of their careers to studying the vacuum. It is
interesting! Anyway, very (very!) roughly, if you put these parallel plates close together, the energy associated with these fields between the plates is less than the energy associated
with the fields outside the plates. The net energy associated with the fields outside the plates is zero (or close to it), since it is the vacuum after all, so the energy between the plates
turns out to be negative. The problem is, this "Casimir" effect is very small and, if you include the energy associated with the metal plates, the total energy of the system is positive,
not negative as required by the warp drive. It is highly unlikely that one can generate enough negative energy using this technique to form a warp bubble. I guess in theory it's possible
but don't hold your breath.
By the way, if you'd like to see what a ship in warp would look like from outside, there is a nice video here (D. Weiskopf, Univ. Tübingen).
One final note before going to Part 2. It was originally thought that, once a warp bubble has been formed and you start "moving" with an apparent speed greater than the speed of light, you
would not be able to send a signal to the warp bubble. That is, once you turned on the warp drive there would be no way to turn it off! In fancy language a horizon exists in the
space-time. It has been shown though (see the paper by Loup et al in the bibliography) that this is not a problem since you can send a signal to part of the warp bubble, slow down to
a sub-luminal apparent velocity and then shut off the bubble completely.
P.S. No, there is no chance of building this with anything even remotely resembling our current technology level. They are just interesting spacetimes to study.
Part 2 Quantitative discussion.
The warp drive metrics, in a Cartesian type coordinate chart are given by the line element:
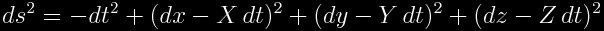 .
.
X, Y, and Z are the components of a vector field defined in Euclidean 3-space. This is a function of the coordinates. Alcubierre (see bibliography) used, as the first
mathematical example of a warp drive, the function:
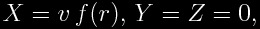
where 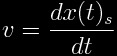 and r is a radial coordinate centered at the ship:
and r is a radial coordinate centered at the ship:
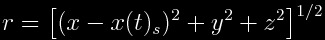 .
.
From this point onward it is useful to use the notation 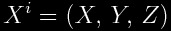 .
.
The function f(r) is a bounded function. Specifically, for the first warp drive, this function is equal to one in the
immediate vicinity of the ship and quickly tends to zero outside the warp bubble (like a "top hat" function). There are
some things to note about this metric. First, t=constant hyper-surfaces are just good old Euclidean space. Second, well
outside the warp bubble, the metric is just that of Minkowski space-time. Also, this metric is constructed via the 3+1 formalism and
therefore does not admit closed causal curves. Finally, Eulerian observers are in free-fall. That is, observers whose four-velocity
is orthogonal to the spatial hypersurfaces are following geodesic paths. In other words, because the spring is
unstretched inside and outside the bubble, gravity is not "pushing around"
the crew members nor the folks outside of the warp bubble.
Since the three-geometry is flat one may study curvature from an extrinsic perspective. The extrinsic curvature tensor of a
t=constant surface is given by:
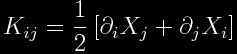 .
.
Now, of interest, of course, is how much the space-time is
being stretched or compressed and, more importantly, what is the value as
measured by the Eulerian observers. It is well known from differential geometry
that the trace of the extrinsic curvature tensor provides this result:
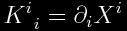 .
.
Let’s call this “the stretching function”. If we plug in the
expressions for the original warp-drive above, this quantity yields:
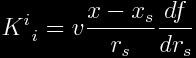 .
.
Note the following: The faster the ship travels, the greater
the stretching function. If we consider a “top hat” like function for f(r), then
the stretching function vanishes outside the warp bubble (the brim) as well as inside
the warp bubble (the “cylinder”). This is good news since we don’t want the
crew nor the people outside the warp bubble to be compressed. The stretching function is
plotted in figure 3. The ship is located at the center of the plot and you
can see how the space around the ship is compressed (in front of the ship where the stretching function is negative) and stretched
(behind, where it is positive). Also note that, if you set dy=dz=0 as well as setting
x=xs, then the line element presented at the beginning of
this section yields the nice result that both inside the warp bubble and
outside the warp bubble
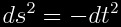 .
.
In other words, proper time inside the ship equals proper
time outside the warp bubble.

The Eulerian observers possess co-variant four-velocity
given by
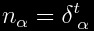 .
.
Therefore, the energy density measured along their world
lines is given by
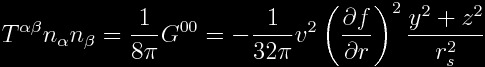 ,
,
where now we are considering the specific case of the
original warp drive. As mentioned in part 1, this quantity is negative. The
faster you go, the “more negative” this gets. Just “how negative” is this and
how can we minimize the amount of negative energy? Well, notice that the derivative
vanishes both inside and outside the warp bubble (not exactly, but close since f
is approximately a “top hat” function). This means that this function is
non-zero only in the immediate vicinity of the warp bubble. If the ship is
large, then (y2+z2)/rs2 is
potentially large or of order unity in the vicinity of the warp bubble. If it
were possible to make this term small, and still encompass a decent sized ship,
we could minimize the amount of negative energy required.
Professor Chris Van Den Broeck (bibliography) modified the original warp drive metric and proposed the following line-element:
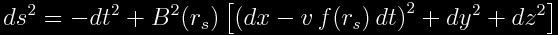 ,
,
where the function B(rs) is chosen as 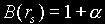 for the region well inside the warp bubble,
for the region well inside the warp bubble, 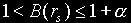 for the region inside the warp bubble but close to the warp bubble (the transition region... this is where the blown up part joins the regular Alcubierre warp drive), and B(rs) =1 from near the inner-wall of the warp bubble and outward. The constant
for the region inside the warp bubble but close to the warp bubble (the transition region... this is where the blown up part joins the regular Alcubierre warp drive), and B(rs) =1 from near the inner-wall of the warp bubble and outward. The constant 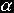 can be large and positive. Notice that this metric encloses an arbitrarily large volume inside the warp bubble. In other words, you can have a small warp bubble (which will therefore require only a small amount of negative energy) but a volume inside the warp bubble which is large enough to hold a spaceship. In the spring model of part 1, the picture would be as in the figure below.
can be large and positive. Notice that this metric encloses an arbitrarily large volume inside the warp bubble. In other words, you can have a small warp bubble (which will therefore require only a small amount of negative energy) but a volume inside the warp bubble which is large enough to hold a spaceship. In the spring model of part 1, the picture would be as in the figure below.
Notice that the region of length L, as well as the compressed and
stretched regions, are now much smaller than in the
previous diagrams (in 3D it is much more obvious that you are compressing
and stretching a smaller region). This means that the negative energy
requirements will
be less. In the transition region the energy density is provided by:
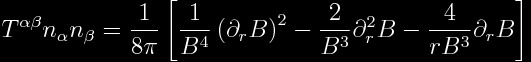 .
.
With an appropriate choice of the function B, one may have a sufficiently smooth geometry in the transition region. Parts of this region, however, must also possess negative energy but the requirements are much less than in the original model. So, here we have a warp drive with a very small "throat" or warp bubble, requiring small negative energies. Inside this bubble a transition region exists between the expanded volume interior and the original warp drive interior. This transition region requires some positive energy and some negative energy but, as mentioned above, these requirements are much less than in the unmodified warp drive.
Now we discuss the negative energy and what quantum field theory has to say about it. We will concentrate on the curious effect we mentioned in part I called the Casimir effect. In curved space-time the situation is a bit daunting therefore we will assume a Minkowski background and neglect gravity. Also, we will concentrate on one of the simplest of quantum fields, the massless scalar field.
The energy associated with the quantum field is given by the integral:
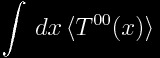
Where < T00 > is the expectation of the energy density of the field. This is actually a divergent quantity if integrated over all space (to get energy) but, of course, it is changes in energy that are important.
Classically, the stress-energy tensor for a massless scalar is given by
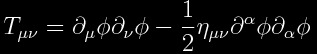 .
.
The analogue in the quantum theory is the expectation value. We therefore need these derivatives in the quantized theory. These are provided by taking derivatives of the Green function of the scalar wave equation:
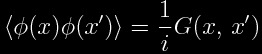
and then taking the limit as x -> x' .
The expectation value of the energy density component of the quantized stress-energy tensor can be calculated to be
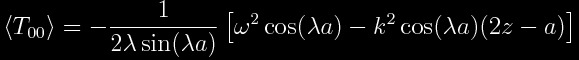 ,
,
where a is the separation width of the plates and 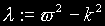 . (omega is the frequency and k is the wave number of the mode.)
. (omega is the frequency and k is the wave number of the mode.)
When we integrate the above in the region between the plates we get:
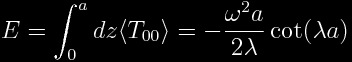 .
.
Here you see that the energy is negative.
Partial Bibliography
P.S. No, there is no chance of building this with anything even remotely resembling our current technology level. They are just interesting spacetimes to study.




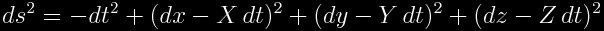 .
.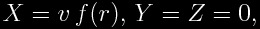
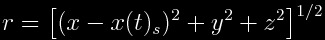 .
. 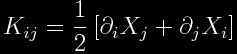 .
.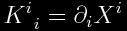 .
.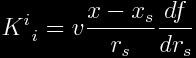 .
.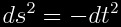 .
.
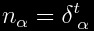 .
.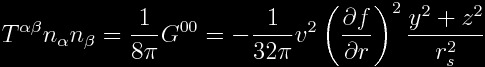 ,
,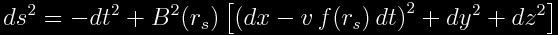 ,
,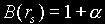 for the region well inside the warp bubble,
for the region well inside the warp bubble, 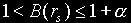 for the region inside the warp bubble but close to the warp bubble (the transition region... this is where the blown up part joins the regular Alcubierre warp drive), and B(rs) =1 from near the inner-wall of the warp bubble and outward. The constant
for the region inside the warp bubble but close to the warp bubble (the transition region... this is where the blown up part joins the regular Alcubierre warp drive), and B(rs) =1 from near the inner-wall of the warp bubble and outward. The constant 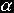 can be large and positive. Notice that this metric encloses an arbitrarily large volume inside the warp bubble. In other words, you can have a small warp bubble (which will therefore require only a small amount of negative energy) but a volume inside the warp bubble which is large enough to hold a spaceship. In the spring model of part 1, the picture would be as in the figure below.
can be large and positive. Notice that this metric encloses an arbitrarily large volume inside the warp bubble. In other words, you can have a small warp bubble (which will therefore require only a small amount of negative energy) but a volume inside the warp bubble which is large enough to hold a spaceship. In the spring model of part 1, the picture would be as in the figure below.
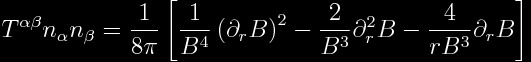 .
. 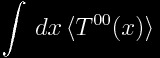
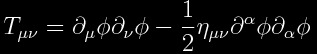 .
.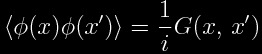
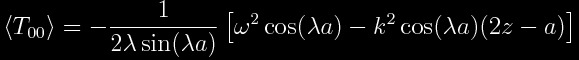 ,
,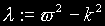 . (omega is the frequency and k is the wave number of the mode.)
. (omega is the frequency and k is the wave number of the mode.)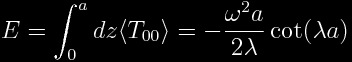 .
.