Postscript version of these notes

STAT 380 Lecture 22

Black Scholes

We model the price of a stock as

where

is a Brownian motion with drift (B is standard Brownian motion).

If annual interest rates are we call the instantaneous interest rate; if we invest $1 at time 0 then at time t we would have . In this sense an amount of money x(t) to be paid at time t is worth only at time 0 (because that much money at time 0 will grow to x(t) by time t).

Present Value: If the stock price at time t is X(t) per share then the present value of 1 share to be delivered at time t is

With X as above we see

Now we compute

for s< t. Write

Since B has independent increments we find

Note: B(t)-B(s) is N(0,t-s); the expected value needed is the moment generating function of this variable at .

Suppose . The Moment Generating Function of U is

Rewrite

where to see

Finally we get

provided

If this identity is satisfied then the present value of the stock price is a martingale.

Option Pricing

Suppose you can pay $c today for the right to pay K for a share of this stock at time t (regardless of the actual price at time t).

If, at time t, X(t) > K you willexercise your option and buy the share making X(t)-K dollars.

If you will not exercise your option; it becomes worthless.

The present value of this option is

where

(Called positive part of z.)

In a fair market:

• The discounted share price is a martingale.
• The expected present value of the option is 0.

So:

Since

we are to compute

This is

where

Evidently

The other integral needed is

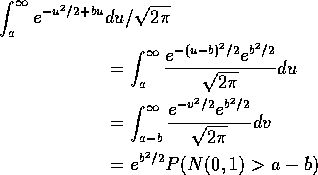
Introduce the notation

and do all the algebra to get

This is the Black-Scholes option pricing formula.