STAT 380 Lecture 25
Inverse (Probability Integral) Transform
Fact: F continuous CDF and X,U satisfy
then 
Uniform(0,1) if and only if 
.
Proof: For simplicity: assume F strictly increasing on inverval (a,b) with F(b)=1 and F(a)=0.
If Uniform(0,1) then
Conversely: if and 0 < u < 1 then
there is a unique x such that F(x) = u
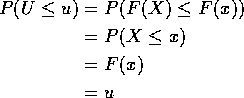
Application: generate U and solve F(X)=U for X
to get 
which has cdf F.
Example: For the exponential distribution
Set F(X) = U and solve to get
Observation: 
so 
also has
an Exponential( 
) distribution.
Example: : for F the standard normal cdf solving
requires numerical approximation but such solutions are built in to many languages.
Special purpose transformations:
Example: : If X and Y are iid N(0,1) define
and 
by
NOTE: Book says
but this takes values in 
; notation
means angle 
in 
so that
Then
is part of circle of radius 
. (Start at 
and go clockwise
to angle 
.)
Compute joint cdf of 
at 
.
Define
Then
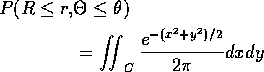
Do integral in polar co-ordinates to get
The integral just gives
The r integral then gives
So
Product of two cdfs so:
R and 
are independent.
Moreover
has cdf
which is Exponential with rate 1/2.
is Uniform 
.
So: generate 
iid Uniform(0,1).
Define
and
Put
You have generated two independent N(0,1) variables.
Acceptance Rejection
If F(X)=U difficult to solve (eg F hard to compute) sometimes use acceptance rejection.
Goal: generate where 
.
Tactic: find density g and constant c such that
and s.t. can generate Y from density g.
Algorithm:
Uniform(0,1) independent of Y.
let X=Y.
Facts:
so
Most important fact: 
:
Proof: this is like the old craps example:
We compute
(condition on the first iteration where the condition is met).
Condition on Y to get
as desired.