
Course outline:
Example 1: Three cards: one red on both sides, one black on both sides, one black on one side, red on the other. Shuffle, pick card at random. Side up is Black. What is the probability the side down is Black?
Solution: To do this carefully, enumerate sample space,
![]() ,
of all possible outcomes. Six sides to the three cards.
Label three red sides 1, 2, 3 with sides 1, 2 on the all red card (card
# 1).
Label three black sides 4, 5, 6 with 3, 4 on opposite sides of mixed
card (card #2). Define some events:
,
of all possible outcomes. Six sides to the three cards.
Label three red sides 1, 2, 3 with sides 1, 2 on the all red card (card
# 1).
Label three black sides 4, 5, 6 with 3, 4 on opposite sides of mixed
card (card #2). Define some events:

One representation
![]() .
Then
.
Then
![]() ,
,
![]() ,
,
![]() and so on.
and so on.
Modelling: assumptions about some probabilities; deduce probabilities of other events. In example simplest model is
Apply two rules:
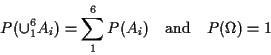
Definition of conditional probability:
Example 2: Monte Hall, Let's Make a Deal. Monte shows you 3 doors. Prize hidden behind one. You pick a door. Monte opens a door you didn't pick; shows you no prize; offers to let you switch to the third door. Do you switch?
Sample space: typical element is (a,b,c) where a is number of door with prize, b is number of your first pick and c is door Monte opens with no prize.
| (1,1,2) | (1,1,3) | (1,2,3) | (1,3,2) |
| (2,1,3) | (2,2,1) | (2,2,3) | (2,3,1) |
| (3,1,2) | (3,2,1) | (3,3,1) | (3,3,2) |
Model? Traditionally we define events like
![]()
and assume that each Ai has chance 1/3. We
are assuming we have no prior reason to suppose
Monte favours one door. But these and all other
probabilities depend on the behaviour of people
so are open to discussion.
The event LS, that you lose if you switch is
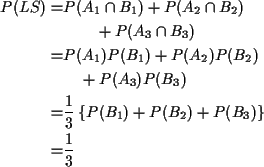
So the event you win by switching has probability 2/3 and you should switch.
Usual phrasing of problem. You pick 1, Monte shows 3. Should
you take 2? Let S be rv S = door Monte
shows you. Question:
Modelling assumptions do not determine this; it depends on Monte's method for choosing door to show when he has a choice. Two simple cases:
Use Bayes' rule:

Numerator is
![]()
Denominator is
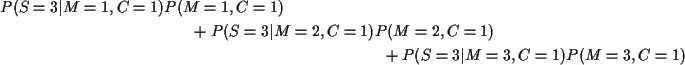
which simplifies to
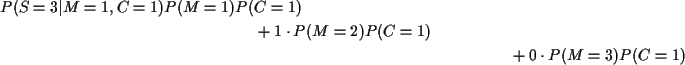
which in turn is
For case 1 we get
Notice that in case 2 if we pick door 1 and Monte shows us door 2 we should definitely switch. Notice also that it would be normal to assume that Monte used the case 1 algorithm to pick the door to show when he has a choice; otherwise he is giving the contestant information. If the contestant knows Monte is using algorithm 2 then by switching if door 2 is shown and not if door 3 is shown he wins 2/3 of the time which is as good as the always switch strategy.
Example 3: Survival of family names. Traditionally: family name follows sons. Given man at end of 20th century. Probability descendant (male) with same last name alive at end of 21st century? or end of 30th century?
Simplified model: count generations not years. Compute probability, of survival of name for n generations.
Technically easier to compute qn, probability of extinction by generation n.
Useful rvs:
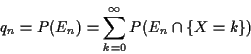
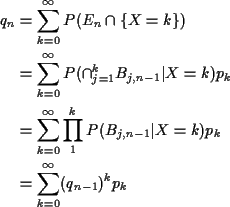
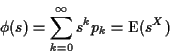
Geometric Distribution: Assume
Then
![\begin{align*}\phi(s) & = \sum_0^\infty s^k (1-\theta)^k \theta
\\
& = \theta \...
...fty \left[s(1-\theta)\right]^k
\\
& = \frac{\theta}{1-s(1-\theta)}
\end{align*}](img41.gif)
Set
![]() to get
to get
Binomial(![]() ): If
): If
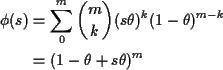
Poisson(![]() ): Now
): Now
Important Points:
Example 3: Mean values
Zn = total number of sons in generation n.
Z0=1 for convenience.
Compute
![]() .
.
Recall definition of expected value:
If X is discrete then
If X is absolutely continuous then
Theorem: If Y=g(X), X has density f then
Key properties of ![]() :
:
1: If ![]() then
then
![]() .
Equals iff
P(X=0)=1.
.
Equals iff
P(X=0)=1.
2:
![]() .
.
3: If
![]() then
then
4:
![]() .
.
Conditional Expectations
If X, Y, two discrete random variables then
Extension to absolutely continuous case:
Joint pmf of X and Y is defined as
Example:
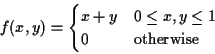
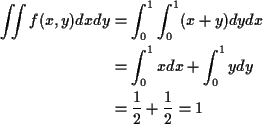
The marginal density of X is, for
![]() .
.
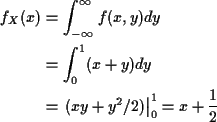
For x not in [0,1] the integral is 0 so
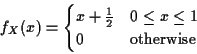
Conditional Densities
If X and Y have joint density
fX,Y(x,y) then
we define the conditional density of Y given X=x by
analogy with our interpretation of densities. We take limits:

in the sense that if we divide through by dy and let
dx and dy tend to 0 the conditional density is the limit
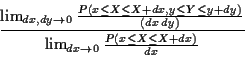
Going back to our interpretation of joint densities and ordinary
densities we see that our definition is just
Example: For f of previous example conditional density
of Y given X=x defined only for
![]() :
:
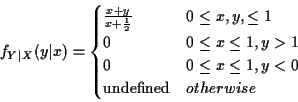
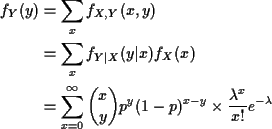
WARNING: in sum
![]() is required and x, y integers
so sum really runs from y to
is required and x, y integers
so sum really runs from y to ![]()
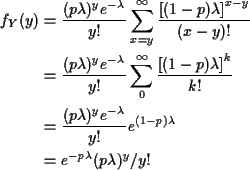
which is a Poisson(![]() )
distribution.
)
distribution.
Conditional Expectations
If X and Y are continuous random variables with joint density
fX,Y we define:
Key properties of conditional expectation
1: If ![]() then
then
![]() .
Equals iff
P(Y=0|X=x)=1.
.
Equals iff
P(Y=0|X=x)=1.
2:
![]() .
.
3: If Y and X are independent then
4:
![]() .
.
Example:
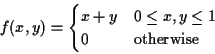
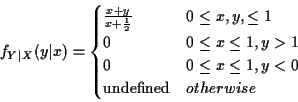
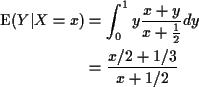
Computing expectations by conditioning:
Notation:
![]() is the function of X you get by
working out
is the function of X you get by
working out
![]() ,
getting a formula in x and replacing
x by X. This makes
,
getting a formula in x and replacing
x by X. This makes
![]() a random variable.
a random variable.
Properties:
1:
![]() .
.
2: If Y and X are independent then
3:
![]() .
.
4:
![]() (compute average
holding X fixed first, then average over X).
(compute average
holding X fixed first, then average over X).
In example:
![\begin{align*}{\rm E}(Z_n) & = {\rm E}\left[{\rm E}(Z_n\vert X)\right]
\\
& = {...
...Z_{n-2})
\\
& \quad \vdots
\\
& = m^{n-1}{\rm E}(Z_1)
\\
& = m^n
\end{align*}](img104.gif)
For m < 1 expect exponential decay. For m>1 exponential growth (if not extinction).
We have reviewed the following definitions:
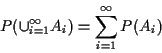
Tactics:
Tactics for expected values:
Last names example has following structure: if, at generation n there are m individuals then the number of sons in the next generation has the distribution of the sum of m independent copies of the random variable X which is the number of sons I have. This distribution does not depend on n, only on the value m of Zn. We call Zn a Markov Chain.
Ingredients of a Markov Chain:
The stochastic process
![]() is called a
Markov chain if
is called a
Markov chain if
The matrix ![]() is called a transition matrix.
is called a transition matrix.
Example: If X in the last names example has
a Poisson![]() distribution then given Zn=k,
Zn+1 is like sum of k independent Poisson
distribution then given Zn=k,
Zn+1 is like sum of k independent Poisson![]() rvs which has a Poisson(
rvs which has a Poisson(![]() )
distribution.
So
)
distribution.
So
![\begin{displaymath}{\bf P}= \left[\begin{array}{llll}
1 & 0 & 0 & \cdots
\\
e^{...
...ts
\\
\vdots &
\vdots &
\vdots &
\ddots
\end{array}\right]
\end{displaymath}](img133.gif)
Example: Weather: each day is dry (D) or wet (W).
Xn is weather on day n.
Suppose dry days tend to be followed by dry days, say 3 times in 5 and wet days by wet 4 times in 5.
Markov assumption: yesterday's weather irrelevant to prediction of tomorrow's given today's.
Transition Matrix:
![\begin{displaymath}{\bf P}= \left[\begin{array}{cc} \frac{3}{5} & \frac{2}{5}
\\
\\
\frac{1}{5} & \frac{4}{5}
\end{array} \right]
\end{displaymath}](img134.gif)
Now suppose it's wet today. P(wet in 2 days)?
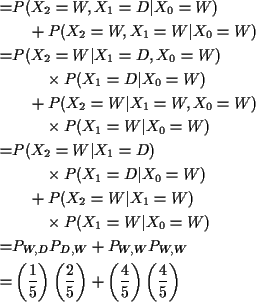
![\begin{displaymath}\left[\begin{array}{ll} \frac{3}{5} & \frac{2}{5}
\\
\\
\fr...
...ac{2}{5}
\\
\\
\frac{1}{5} & \frac{4}{5}
\end{array} \right]
\end{displaymath}](img138.gif)
General case. Define
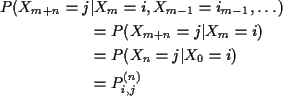
Proof of these assertions by induction on m,n.
Example for n=2. Two bits to do:
First suppose U,V,X,Y are discrete variables.
Assume
![]()
for any x,y,u,v. Then I claim
![]()
In words, if knowing both U and V doesn't change the
conditional probability then knowing U alone doesn't
change the conditional probability.
Proof of claim:
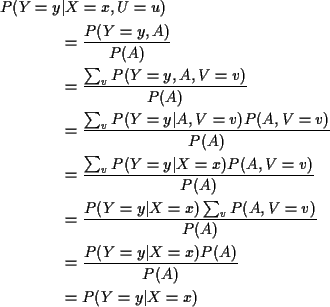
Second step: consider
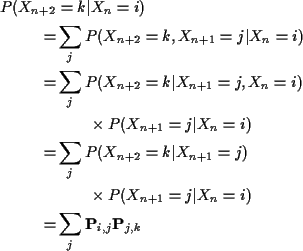
This shows that
More general version

Summary: A Markov Chain has stationary n step transition probabilities which are the nth power of the 1 step transition probabilities.
Here is Maple output for the 1,2,4,8 and 16 step transition matrices for our rainfall example:
> p:= matrix(2,2,[[3/5,2/5],[1/5,4/5]]);
[3/5 2/5]
p := [ ]
[1/5 4/5]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> p16:=evalm(p8*p8):
This computes the powers (evalm understands
matrix algebra).
Fact:
![\begin{displaymath}\lim_{n\to\infty} {\bf P}^n = \left[
\begin{array}{cc} \frac{...
...ac{2}{3}
\\
\\
\frac{1}{3} & \frac{2}{3}
\end{array}\right]
\end{displaymath}](img150.gif)
> evalf(evalm(p));
[.6000000000 .4000000000]
[ ]
[.2000000000 .8000000000]
> evalf(evalm(p2));
[.4400000000 .5600000000]
[ ]
[.2800000000 .7200000000]
> evalf(evalm(p4));
[.3504000000 .6496000000]
[ ]
[.3248000000 .6752000000]
> evalf(evalm(p8));
[.3337702400 .6662297600]
[ ]
[.3331148800 .6668851200]
> evalf(evalm(p16));
[.3333336197 .6666663803]
[ ]
[.3333331902 .6666668098]
Where did 1/3 and 2/3 come from?
Suppose we toss a coin
![]() and start the
chain with Dry if we get heads and Wet if we get
tails.
and start the
chain with Dry if we get heads and Wet if we get
tails.
Then
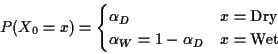
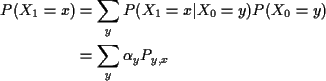
![\begin{displaymath}\left[ \frac{1}{3} \quad \frac{2}{3} \right]
\left[\begin{ar...
...array} \right] = \left[ \frac{1}{3} \quad \frac{2}{3} \right]
\end{displaymath}](img157.gif)
A probability vector ![]() is called an initial distribution for
the chain if
is called an initial distribution for
the chain if
A Markov Chain is stationary if
An initial distribution is called stationary if the chain is
stationary. We find that ![]() is a stationary initial distribution
if
is a stationary initial distribution
if
Suppose ![]() converges to some matrix
converges to some matrix
![]() .
Notice that
.
Notice that
![\begin{align*}{\bf P}^\infty & = \lim {\bf P}^n
\\
& = \left[\lim {\bf P}^{n-1}\right] {\bf P}
\\
& = {\bf P}^\infty {\bf P}
\end{align*}](img163.gif)
This proves that each row ![]() of
of
![]() satisfies
satisfies
Def'n: A row vector x is a left eigenvector of A with
eigenvalue ![]() if
if
So each row of
![]() is a left eigenvector of
is a left eigenvector of ![]() with eigenvalue 1.
with eigenvalue 1.
Finding stationary initial distributions. Consider the ![]() for the weather example. The equation
for the weather example. The equation
![\begin{displaymath}{\bf P}= \left[\begin{array}{cccc}
0 & 1/3 & 0 & 2/3
\\
1/3...
...\\
0 & 2/3 & 0 & 1/3
\\
2/3 & 0 & 1/3 & 0
\end{array}\right]
\end{displaymath}](img171.gif)
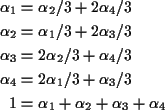
p:=matrix([[0,1/3,0,2/3],[1/3,0,2/3,0],
[0,2/3,0,1/3],[2/3,0,1/3,0]]);
[ 0 1/3 0 2/3]
[ ]
[1/3 0 2/3 0 ]
p := [ ]
[ 0 2/3 0 1/3]
[ ]
[2/3 0 1/3 0 ]
> p2:=evalm(p*p);
[5/9 0 4/9 0 ]
[ ]
[ 0 5/9 0 4/9]
p2:= [ ]
[4/9 0 5/9 0 ]
[ ]
[ 0 4/9 0 5/9]
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> p16:=evalm(p8*p8):
> p17:=evalm(p8*p8*p):
> evalf(evalm(p16));
[.5000000116 , 0 , .4999999884 , 0]
[ ]
[0 , .5000000116 , 0 , .4999999884]
[ ]
[.4999999884 , 0 , .5000000116 , 0]
[ ]
[0 , .4999999884 , 0 , .5000000116]
> evalf(evalm(p17));
[0 , .4999999961 , 0 , .5000000039]
[ ]
[.4999999961 , 0 , .5000000039 , 0]
[ ]
[0 , .5000000039 , 0 , .4999999961]
[ ]
[.5000000039 , 0 , .4999999961 , 0]
> evalf(evalm((p16+p17)/2));
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
![\begin{displaymath}p = \left[\begin{array}{cccc}
\frac{2}{5} & \frac{3}{5}
& 0 &...
...{3}{5}
\\
0 &0 &
\frac{1}{5} & \frac{4}{5}\end{array}\right]
\end{displaymath}](img177.gif)
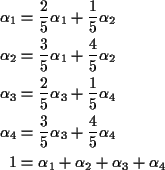
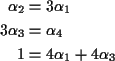
Pick ![]() in [0,1/4];
put
in [0,1/4];
put
![]() .
.
> p:=matrix([[2/5,3/5,0,0],[1/5,4/5,0,0],
[0,0,2/5,3/5],[0,0,1/5,4/5]]);
[2/5 3/5 0 0 ]
[ ]
[1/5 4/5 0 0 ]
p := [ ]
[ 0 0 2/5 3/5]
[ ]
[ 0 0 1/5 4/5]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> evalf(evalm(p8*p8));
[.2500000000 , .7500000000 , 0 , 0]
[ ]
[.2500000000 , .7500000000 , 0 , 0]
[ ]
[0 , 0 , .2500000000 , .7500000000]
[ ]
[0 , 0 , .2500000000 , .7500000000]
Notice that rows converge but to two different vectors:
> p:=matrix([[2/5,3/5,0],[1/5,4/5,0],
[1/2,0,1/2]]);
[2/5 3/5 0 ]
[ ]
p := [1/5 4/5 0 ]
[ ]
[1/2 0 1/2]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> evalf(evalm(p8*p8));
[.2500000000 .7500000000 0 ]
[ ]
[.2500000000 .7500000000 0 ]
[ ]
[.2500152588 .7499694824 .00001525878906]
Basic distinguishing features: pattern of 0s in matrix ![]() .
.
State i leads to state j if
![]() for some n.
It is convenient to agree that
for some n.
It is convenient to agree that
![]() the identity matrix;
thus i leads to i.
the identity matrix;
thus i leads to i.
Note i leads to j and j leads to k implies i leads to k(Chapman-Kolmogorov).
States i and j communicate if i leads to j and j leads to i.
The relation of communication is an equivalence relation; it is reflexive, symmetric and transitive: if i and j communicate and j and k communicate then i and kcommunicate.
Example (+ signs indicate non-zero entries):
![\begin{displaymath}{\bf P}= \left[\begin{array}{ccccc}
0& 1 & 0 & 0 &0
\\
0 & 0...
...\\
+ & 0 & 0 & + & 0
\\
0 & + & 0 & + & +
\end{array}\right]
\end{displaymath}](img192.gif)
For this example:
![]() ,
,
![]() ,
,
![]() so 1,2,3 are all in the same communicating class.
so 1,2,3 are all in the same communicating class.
![]() but not vice versa.
but not vice versa.
![]() but not vice versa.
but not vice versa.
So the communicating classes are
A Markov Chain is irreducible if there is only one communicating class.
Notation:
State i is recurrent if fi=1, otherwise transient.
If fi=1 then Markov property (chain starts over when it gets back to i) means prob return infinitely many times (given started in i or given ever get to i) is 1.
Consider chain started from transient i.
Let N be number of visits
to state i (including visit at time 0). To return m-1 times must return once
then starting over return m-1 times, then never return.
So:
N has a Geometric distribution and
![]() .
.
Another calculation:
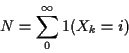
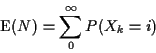
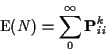
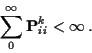
For last example: 4 and 5 are transient. Claim: states 1, 2 and 3 are recurrent.
Proof: argument above shows each transient state is visited only finitely many times. So: there is a recurrent state. (Note use of finite number of states.) It must be one of 1, 2 and 3. Proposition: If one state in a communicating class is recurrent then all states in the communicating class are recurrent.
Proof: Let i be the known recurrent state so
Proposition also means that if 1 state in a class is transient so are all.
State i has period d if d is greatest common
divisor of
![\begin{displaymath}{\bf P}= \left[\begin{array}{ccccc}
0& 1 & 0 & 0 &0
\\
0 & 0...
...\\
0 & 0 & 0 & 0 & 1
\\
0 & 0 & 0 & 1 & 0
\end{array}\right]
\end{displaymath}](img212.gif)
![\begin{displaymath}{\bf P}= \left[\begin{array}{ccc}
0& 1/2 & 1/2
\\
1 & 0 & 0
\\
1 & 0 & 0
\end{array}\right]
\end{displaymath}](img215.gif)
A chain is aperiodic if all its states are aperiodic.
Example: consider a sequence of independent coin tosses with probability pof Heads on a single toss. Let Xn be number of heads minus number of tails after n tosses. Put X0=0.
Xn is a Markov Chain. State space is ![]() ,
the integers and
,
the integers and
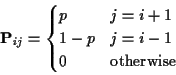
This chain has one communicating class (for ![]() )
and
all states have period 2. According to the strong law of large
numbers Xn/n converges to 2p-1. If
)
and
all states have period 2. According to the strong law of large
numbers Xn/n converges to 2p-1. If ![]() this guarantees
that for all large enough n
this guarantees
that for all large enough n
![]() ,
that is, the number
of returns to 0 is not infinite. The state 0 is then transient
and so all states must be transient.
,
that is, the number
of returns to 0 is not infinite. The state 0 is then transient
and so all states must be transient.
For p = 1/2 the situation is different. It is a fact that
Local Central Limit Theorem (normal approximation to
P(-1/2 < Xn < 1/2)) (or Stirling's approximation) shows
Start irreducible recurrent chain Xn in state i.
Let Tj be first n>0 such that Xn=j.
Define
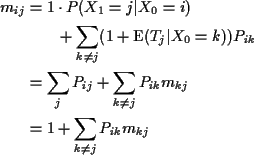
Example
![\begin{displaymath}{\bf P}= \left[\begin{array}{cc} \frac{3}{5} & \frac{2}{5}
\\
\\
\frac{1}{5} & \frac{4}{5}
\end{array} \right]
\end{displaymath}](img134.gif)
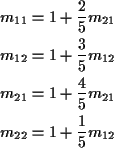
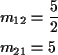
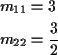
Notice stationary initial distribution is
Heuristic: start chain in i. Expect to return to i every mii time units. So are in state i about once every mii time units; i.e. limiting fraction of time in state iis 1/mii.
Conclusion: for an irreducible recurrent finite state space
Markov chain
Previous conclusion is still right if there is a stationary initial distribution.
Example:
![]() after n tosses
of fair coin. Equations are
after n tosses
of fair coin. Equations are
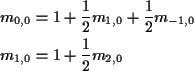
and many more.
Some observations:
You have to go through 1 to get to 0 from 2 so
Symmetry (switching H and T):
The transition probabilities are homogeneous:
Conclusion:
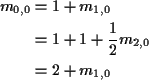
Notice that there are no finite solutions!
Summary of the situation:
Every state is recurrent.
All the expected hitting times mij are infinite.
All entries
![]() converge to 0.
converge to 0.
Jargon: The states in this chain are null recurrent.
Page 229, question 21: runner goes from front or back door, prob 1/2 each. Returns front or back, prob 1/2 each. Has k pairs of shoes, wears pair if any at departure door, leaves at return door. No shoes? Barefoot. Long run fraction of time barefoot?
Solution: Let Xn be number of shoes at front door on day n. Then Xn is a Markov Chain.
Transition probabilities:
k pairs at front door on day n. Xn+1 is k if goes out back door (prob is 1/2) or out front door and back in front door (prob is 1/4). Otherwise Xn+1 is k-1.
0 < j < k pairs at front door on day n. Xn+1 is j+1if out back, in front (prob is 1/4). Xn+1 is j-1 if out front, in back. Otherwise Xn+1 is j.
0 pairs at front door on day n. Xn+1 is 0 if out front door (prob 1/2) or out back door and in back door (prob 1/4) otherwise Xn+1 is 1.
Transition matrix ![]() :
:
![\begin{displaymath}\left[\begin{array}{cccccc}
\frac{3}{4} & \frac{1}{4} & 0 & 0...
... 0 & 0 & \cdots & \frac{1}{4} & \frac{3}{4}
\end{array}\right]
\end{displaymath}](img239.gif)
Doubly stochastic: row sums and column sums are 1.
So
![]() for all i is stationary initial distribution.
for all i is stationary initial distribution.
Solution to problem: 1 day in k+1 no shoes at front door. Half of those go barefoot. Also 1 day in k+1 all shoes at front door; go barefoot half of these days. Overall go barefoot 1/(k+1) of the time.
Insurance company's reserves fluctuate: sometimes up, sometimes down. Ruin is event they hit 0 (company goes bankrupt). General problem. For given model of fluctuation compute probability of ruin either eventually or in next k time units.
Simplest model: gambling on Red at Casino. Bet $1 at a time. Win
$1 with probability p, lose $1 with probability 1-p. Start with
k dollars. Quit playing
when down to $0 or up to N. Compute
Xn = fortune after n plays. X0=k.
Transition matrix:
![\begin{displaymath}{\bf P}=
\left[\begin{array}{cccccc}
1 & 0 & 0 & 0 &\cdots &...
...ots & \vdots
\\
0 & 0 & 0 & \cdots & 0 & 1
\end{array}\right]
\end{displaymath}](img242.gif)
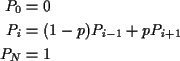
Middle equation is
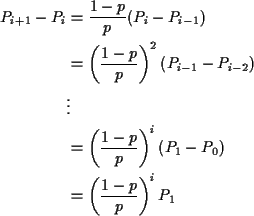
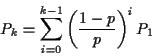
For k=N we get
Notice that if p=1/2 our formulas for the sum of the geometric series
are wrong. But for p=1/2 we get
![\begin{displaymath}{\bf P}= \left[\begin{array}{cccc}
\frac{1}{2} & \frac{1}{2} ...
... & \frac{1}{4} & \frac{3}{8} & \frac{1}{8}
\end{array}\right]
\end{displaymath}](img250.gif)
For i=1 or i=2 and j=3 or 4:
For j=1 or j=2
For
![]() first step analysis:
first step analysis:
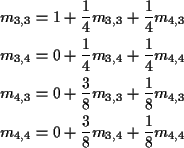
In matrix form
![\begin{align*}\left[\begin{array}{cc} m_{3,3} &m_{3,4} \\ \\
m_{4,3} &m_{4,4}\e...
...ray}{cc} m_{3,3} &m_{3,4} \\ \\
m_{4,3} &m_{4,4}\end{array}\right]
\end{align*}](img254.gif)
Translate to matrix notation:
Solution is
![\begin{displaymath}{\bf I} - {\bf P}_T =
\left[\begin{array}{rr} \frac{3}{4} &...
...rac{1}{4} \\ \\
-\frac{3}{8} & \frac{7}{8}
\end{array}\right]
\end{displaymath}](img260.gif)
![\begin{displaymath}{\bf M} = \left[\begin{array}{rr} \frac{14}{9} & -\frac{4}{9} \\ \\
-\frac{2}{3} & \frac{4}{3}
\end{array}\right]
\end{displaymath}](img261.gif)
Particles arriving over time at a particle detector. Several ways to describe most common model.
Approach 1: numbers of particles arriving in an interval has Poisson distribution, mean proportional to length of interval, numbers in several non-overlapping intervals independent.
For s<t, denote number of arrivals in (s,t] by N(s,t). Model is
Approach 2:
Let
![]() be the times at which the particles
arrive.
be the times at which the particles
arrive.
Let Ti = Si-Si-1 with S0=0 by convention.
Then
![]() are independent Exponential random variables with mean
are independent Exponential random variables with mean ![]() .
.
Note
![]() is called survival function of Ti.
is called survival function of Ti.
Approaches are equivalent. Both are deductions of a model based on local behaviour of process.
Approach 3: Assume:
All 3 approaches are equivalent. I show: 3 implies 1, 1 implies 2 and 2 implies 3. First explain o, O.
Notation: given functions f and g we write
[Aside: if there is a constant M such that
Model 3 implies 1: Fix t, define ft(s) to be conditional probability of 0 points in (t,t+s] given value of process on [0,t].
Derive differential equation for
f. Given process on [0,t] and 0 points in (t,t+s] probability of no
points in (t,t+s+h] is
Notice: survival function of exponential rv..
General case:
Notation: N(t) =N(0,t).
N(t) is a non-decreasing function of t. Let
Given N(t)=j probability that N(t+h) = k is conditional probability of k-j points in (t,t+h].
So, for ![]() :
:
![]()
For j=k-1 we have
![]()
For j=k we have
![]()
N is increasing so only consider ![]() .
.
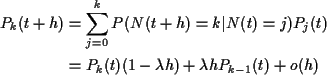
Rearrange, divide by h and let ![]() t get
t get
With P1(0)=0 we get
Similar ideas permit proof of

From which (by induction) we can prove that Nhas independent Poisson increments.
If N is a Poisson Process we define
![]() to be the times between 0 and the first point, the first point and
the second and so on.
to be the times between 0 and the first point, the first point and
the second and so on.
Fact:
![]() are iid exponential rvs with
mean
are iid exponential rvs with
mean ![]() .
.
We already did T1 rigorously. The event T>t is exactly the
event N(t)=0. So
I do case of T1,T2. Let t1,t2 be two positive numbers and
s1=t1,
s2=t1+t2. The event
This is almost the same
as the intersection of the four events:
![\begin{align*}N(0,t_1]&=0
\\
N(t_1,t_1+\delta_1] & = 1
\\
N(t_1+\delta_1,t_1+\delta_1+t_2] & =0
\\
N(s_2+\delta_1,s_2+\delta_1+\delta_2] & = 1
\end{align*}](img301.gif)
which has probability
More rigor:
First step: Compute
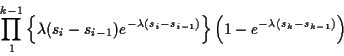
Second step: write this in terms of joint cdf of
![]() .
I do k=2:
.
I do k=2:
![]()
Notice tacit assumption s1 < s2.
Differentiate twice, that is, take

That completes the first part.
Now compute the joint cdf of T1,T2 by
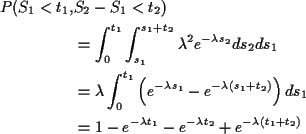
Summary so far:
Have shown:
Instantaneous rates model implies independent Poisson increments model implies independent exponential interarrivals.
Next: show independent exponential interarrivals implies the instantaneous rates model.
Suppose
![]() iid exponential rvs with means
iid exponential rvs with means ![]() .
Define
Nt by Nt=k if and only if
.
Define
Nt by Nt=k if and only if
Let A be the event
![]() .
We
are to show
.
We
are to show
If n(s) is a possible trajectory consistent with N(t) = kthen n has jumps at points
So given
![]() with n(t)=k we are essentially being given
with n(t)=k we are essentially being given
![\begin{align*}P(N(t,t+h] = 1\vert& N(t)=k,A) /h
\\
& = P(B\vert T_{k+1}> t-s_k)/h
\\
& = \frac{P(B) }{he^{-\lambda(t-s_k)}}
\end{align*}](img328.gif)
The numerator may be evaluated by integration:
The computation of
Convolution: If
![]() iid Exponential
iid Exponential![]() then
then
![]() has a Gamma
has a Gamma
![]() distribution. Density
of Sn is
distribution. Density
of Sn is
Proof:
![]()
Then
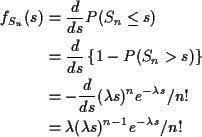
Extreme Values: If
![]() are independent exponential rvs
with means
are independent exponential rvs
with means
![]() then
then
![]() has an exponential distribution with
mean
has an exponential distribution with
mean
Proof:
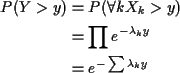
Memoryless Property: conditional distribution of
X-x given ![]() is
exponential if X has an exponential distribution.
is
exponential if X has an exponential distribution.
Proof:
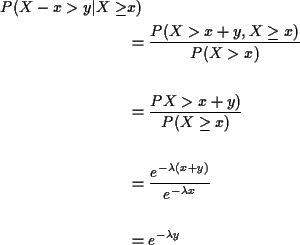
The hazard rate, or instantaneous failure rate for a positive
random variable T with density f and cdf F is
Weibull random variables have density
Since