STAT 380
Problems: Assignment 2
Postscript version of these questions
- 1.
- page 85, number 25, page 85, number 26 and page 87, number 40.
- 2.
- page 146, number 8.
- 3.
- Suppose X and Y are independent Geometric(p) random variables.
In other words for non-negative integers j and k
- (a)
- Let
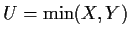 ,
,
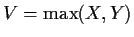 and W=V-U. Express the event
U=j and W=k in terms of X and Y.
and W=V-U. Express the event
U=j and W=k in terms of X and Y.
- (b)
- Compute
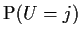 and
and
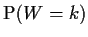 and prove that the event
U=j and the event W=k are independent. You will have to be careful of
the case k=0.
and prove that the event
U=j and the event W=k are independent. You will have to be careful of
the case k=0.
- (c)
- A computer is waiting for two flags to be set. Both flags start
out not set.
For each flag the conditional probability that the flag is set next cycle
given it is not yet set is 0.5. The two flags operate independently. How
many cycles should you expect to wait before both flags are set including
the cycle on which the last flag becomes set?
- 4.
- page 145, number 5.
- 5.
- page 146, number 11.
- 6.
- page 146, number 15.
- 7.
- page 150, number 33.
Richard Lockhart
2000-09-18
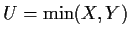 ,
,
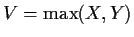 and W=V-U. Express the event
U=j and W=k in terms of X and Y.
and W=V-U. Express the event
U=j and W=k in terms of X and Y.
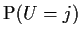 and
and
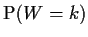 and prove that the event
U=j and the event W=k are independent. You will have to be careful of
the case k=0.
and prove that the event
U=j and the event W=k are independent. You will have to be careful of
the case k=0.