STAT 380
Midterm Examination
Richard Lockhart 20 February 2002
=1=Instructions:
This is an open book exam. You may use notes,
books and a calculator. The exam is out of 25. Questions 1 and 3 are
worth 5 marks each. Each of the 5 parts of question 2 is worth 3 marks.
I will be marking for clarity of
explanation as well as correctness. Without a clear explanation you should
not expect to get more than half marks.
- 1.
- A Markov Chain has state space
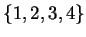 and transition matrix
and transition matrix
Identify all the communicating classes and say whether or not
each is transient. [5 marks]
- 2.
- Each day I get a random number of pieces of voice mail. I deal
with, and delete, a random number of pieces of voice mail. When the mail
box gets full any further messages received are lost. Here is a simplified
model. Assume that my mail box can hold two messages. Each morning I get
either 1 message or 0 messages. Each evening I delete either 1 message
or 0 messages. The probability that I get 1 message is p regardless of
what has happened in the past. The probability that I delete 1 message is
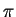 if there is a message to delete. Let Xn be the number of messages
on day n in the morning before any message arrives. Assume that
X0=0; day 0 is the starting day.
if there is a message to delete. Let Xn be the number of messages
on day n in the morning before any message arrives. Assume that
X0=0; day 0 is the starting day.
- (a)
- Write out the transition matrix of the resulting Markov Chain. [3
marks]
- (b)
- Suppose
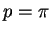 and compute
the probability that the mailbox is empty in the morning on day 2 (before
the arrival of any mail). [3 marks]
and compute
the probability that the mailbox is empty in the morning on day 2 (before
the arrival of any mail). [3 marks]
- (c)
- Again supposing
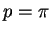 ,
show that in the long run
the fraction of days on which I lose an email is p/3. [3 marks]
,
show that in the long run
the fraction of days on which I lose an email is p/3. [3 marks]
[NOTE: This question was wrong; you should just compute the correct
fraction.]
- (d)
- Again supposing
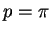 ,
in the long run what fraction of
my e-mail will be lost? [3 marks]
,
in the long run what fraction of
my e-mail will be lost? [3 marks]
- (e)
- Let T be the number of days till I lose my first e-mail and let
mk be the expected value of T given that I start in state k (for
k=0,1,2). Use first step analysis to derive a set of equations which
would be solved to compute the mk. DO NOT SOLVE THE EQUATIONS. [3
marks]
- 3.
- Imagine that buses arrive at a particular stop according to a
Poisson process with rate 2 per hour. I start waiting at the stop at
1:00. Given that the second bus arrives between 2:00 and 3:00 what is the
probability that the first bus arrived before 2:00? You may leave your
answer as a formula--do not bother plugging the numbers into the
calculator. [5 marks]
Extra space
Richard Lockhart
2002-02-26
![\begin{displaymath}\left[\begin{array}{cccc}
\frac{1}{3} & \frac{1}{3} & 0 & \fr...
...frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{2}
\end{array}\right]
\end{displaymath}](img2.gif)
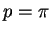 and compute
the probability that the mailbox is empty in the morning on day 2 (before
the arrival of any mail). [3 marks]
and compute
the probability that the mailbox is empty in the morning on day 2 (before
the arrival of any mail). [3 marks]
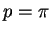 ,
show that in the long run
the fraction of days on which I lose an email is p/3. [3 marks]
,
show that in the long run
the fraction of days on which I lose an email is p/3. [3 marks]
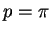 ,
in the long run what fraction of
my e-mail will be lost? [3 marks]
,
in the long run what fraction of
my e-mail will be lost? [3 marks]