![\begin{displaymath}\left[\begin{array}{cccc}
\frac{1}{3} & \frac{1}{3} & 0 & \fr...
...frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{2}
\end{array}\right]
\end{displaymath}](img2.gif)
Identify all the communicating classes and say whether or not each is transient. [5 marks]
Solution: Since 2 leads only to 2 one class is ![]() .
Similarly
3 leads only to 3 and must be in a class of its own,
.
Similarly
3 leads only to 3 and must be in a class of its own,
![]() .
Finally 1 and 4 lead to each other so
.
Finally 1 and 4 lead to each other so ![]() is
the last class. The classes 2 and 3 are recurrent
while
is
the last class. The classes 2 and 3 are recurrent
while ![]() is transient.
is transient.
- (a)
- Write out the transition matrix of the resulting Markov Chain. [3
marks]
Solution: Clearly P02=P20=0. If you start the morning with no voice mail then you end the day with 1 voice mail if a piece of mail comes and you don't delete it. This makes
 .
Similarly
.
Similarly
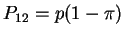 .
Since the rows must sum to 1 we find
.
Since the rows must sum to 1 we find
 .
If I start the day with 1 voice mail I will end the day with 0 voice mails provided
no voice mail arrives and I delete the one I already have; the probability of this is
.
If I start the day with 1 voice mail I will end the day with 0 voice mails provided
no voice mail arrives and I delete the one I already have; the probability of this is
 .
This makes
.
This makes
 .
Finally: if I start the day with 2 voice mails any arriving voice mail will be discarded
so that I will end up at 1 voice mail at the end of the day if I delete a voice mail
that day; thus
.
Finally: if I start the day with 2 voice mails any arriving voice mail will be discarded
so that I will end up at 1 voice mail at the end of the day if I delete a voice mail
that day; thus
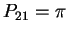 .
Putting it together get
.
Putting it together get
![\begin{displaymath}{\bf P} = \left[\begin{array}{ccc}
1-p(1-\pi) & p(1-\pi) & 0
...
...1-p)(1-\pi) & p(1-\pi)
\\
0 & \pi & 1-\pi
\end{array}\right]
\end{displaymath}](img13.gif)
A common mistake will be to think that .
(This is the
mistake I made in doing the problem when I made it up; with the mistake
in place part c is much easier!)
.
(This is the
mistake I made in doing the problem when I made it up; with the mistake
in place part c is much easier!)
- (b)
- Suppose
 and compute
the probability that the mailbox is empty in the morning on day 2 (before
the arrival of any mail). [3 marks]
and compute
the probability that the mailbox is empty in the morning on day 2 (before
the arrival of any mail). [3 marks]
Solution: You need
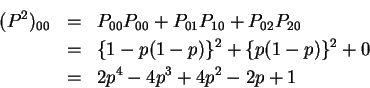
I didn't need to see that last line. - (c)
- Again supposing
 ,
show that in the long run
the fraction of days on which I lose an email is p/3. [3 marks]
,
show that in the long run
the fraction of days on which I lose an email is p/3. [3 marks]
Solution: I made a mistake here. When I created the exam I thought I was making
 doubly stochastic in which case the
stationary initial distribution would be
doubly stochastic in which case the
stationary initial distribution would be

Instead we solve

The first equation gives .
The second
gives
.
The second
gives
 .
Thus
.
Thus
 or
or

The long run fraction of days I start with the mail box full is (1-p)/(3-p); I lose an email on the fraction p of those days when I get an voice mail so I lose

- (d)
- Again supposing
 ,
in the long run what fraction of
my e-mail will be lost? [3 marks]
,
in the long run what fraction of
my e-mail will be lost? [3 marks]
Solution: In the first n days I will get about np pieces of voice mail and I will lose about np(1-p)/(3-p) pieces of voice mail. The answer is the ratio which is (1-p)/(3-p). (This answer is not valid for p=0 which corresponds to never getting or deleting voice mail.
- (e)
- Let T be the number of days till I lose my first e-mail and let
mk be the expected value of T given that I start in state k (for
k=0,1,2). Use first step analysis to derive a set of equations which
would be solved to compute the mk. DO NOT SOLVE THE EQUATIONS. [3
marks]
Solution: If you start the day in state 2 there is a chance pthat T=0 because a piece of mail arrives. If no mail arrives and you don't delete any (probability
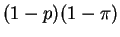 )
then you have used one day
and should still expect to require m2 days more. If no mail arrives
and you delete one piece (probability
)
then you have used one day
and should still expect to require m2 days more. If no mail arrives
and you delete one piece (probability  )
then you have used a
day and should expect to wait m1 more days. Thus
)
then you have used a
day and should expect to wait m1 more days. Thus

If you start the day in state 0 or 1 the situation is easier. You will use your first day and then require mj more days if you go to state jThus
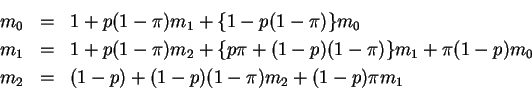
Solution: You are given the information
![]() and
and
![]() which is the union of two events:
which is the union of two events:
and
You want
![\begin{align*}P(N(0,1]\ge 1\vert A_0\cup A_1) & =
\frac{P(N(0,1]\ge 1; N(0,1] ...
...a})}{ 1-e^{-\lambda} - 2\lambda e^{-\lambda} +\lambda
e^{-\lambda}}
\end{align*}](img33.gif)
Plug in 2 for