STAT 380
Midterm Examination
Richard Lockhart 18 October 2000
=1=Instructions:
This is an open book exam. You may use notes,
books and a calculator. The exam is out of 25, 5 marks per question.
I will be marking for clarity of
explanation as well as correctness.
- 1.
- Consider the following strategy for
comparing two medical treatments, say treatment A and treatment B.
Patients are treated one at a time and the result of each treatment is
recorded as a Success or a Failure. Every time a treatment succeeds the
next patient is treated with the same treatment which was just successful.
When a treatment fails, the next patient is treated with the other
treatment. Suppose that the probability that treatment A succeeds is
pA while the probability that treatment B succeeds is pB.
In the long run what fraction of patients are treated with treatment B?
- 2.
- With the same set up as in the first question suppose that
the treatment is changed only after two consecutive failures.
Using the four states:
- 0
- About to use A, last trial was not a failure with A.
- 1
- About to use A, last trial was a failure with A.
- 2
- About to use B, last trial was not a failure with B.
- 3
- About to use B, last trial was a failure with B.
give the transition matrix of a Markov Chain which can be used to
determine what fraction of patients are treated with treatment B in the
long run and show clearly what equations you would solve to
find the answer. You need not actually solve the equations but
I don't want the equations left in matrix form.
- 3.
- A Markov Chain has state space
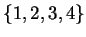 and transition matrix
and transition matrix
- (a)
- Identify all the communicating classes and say whether or not
each is transient.
- (b)
- Let
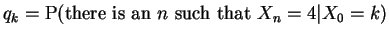 .
Derive the equations
.
Derive the equations
- 4.
- Cosmic rays are detected by a particle detector according to a Poisson
Process with rate 2. An arriving cosmic ray is detected with
probability 0.8 independent of all other cosmic rays and the time at which
the cosmic ray arrives. Compute
the probability that 4 cosmic rays arrived in a time period of length t=5 starting
from time t=0 given that
given that 8 cosmic rays were detected in the time period from t=0 to t=8.
Extra space
Richard Lockhart
2002-02-15
![\begin{displaymath}\left[\begin{array}{cccc}
1 & 0 & 0 & 0
\\
\\
\frac{1}{3} &...
...{1}{2} & \frac{1}{4}
\\
\\
0 & 0 & 0 & 1
\end{array}\right]
\end{displaymath}](img2.gif)
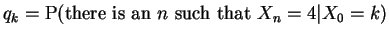 .
Derive the equations
.
Derive the equations