STAT 380

Midterm Examination

Richard Lockhart 18 October 2000

=1=Instructions: This is an open book exam. You may use notes, books and a calculator. The exam is out of 25, 5 marks per question. I will be marking for clarity of explanation as well as correctness.

1.

Consider the following strategy for comparing two medical treatments, say treatment A and treatment B. Patients are treated one at a time and the result of each treatment is recorded as a Success or a Failure. Every time a treatment succeeds the next patient is treated with the same treatment which was just successful. When a treatment fails, the next patient is treated with the other treatment. Suppose that the probability that treatment A succeeds is p_A while the probability that treatment B succeeds is p_B. In the long run what fraction of patients are treated with treatment B?

Solution: If X_n is the treatment used on patient n+1 then X_n is a Markov chain with transition matrix

$${\bf p} = \left[\begin{array}{cc} p_A & 1-p_A \\ 1-p_b & p_B\end{array}\right]$$

The stationary initial distribution is $(\pi_A,\pi_B)$ with $\pi_A=1-\pi_B$. It satisfies
$$\begin{align*}\pi_B &= \pi_A (1-p_A)+ \pi_Bp_B \\ & = 1-p_a+\pi_B(p_B-(1-p_A)) \\ & = 1-p_a+\pi_B(p_A+p_B-1) \end{align*}$$
The solution is

$$\pi_B = \frac{1-p_A}{2-p_A-p_B}$$

and this is the long run fraction of the time that treatment B is used.

2.

With the same set up as in the first question suppose that the treatment is changed only after two consecutive failures. Using the four states:

0

About to use A, last trial was not a failure with A.

1

About to use A, last trial was a failure with A.

2

About to use B, last trial was not a failure with B.

3

About to use B, last trial was a failure with B.

give the transition of a Markov Chain which can be used to determine what fraction of patients are treated with treatment B in the long run and show clearly what equations you would solve to find the answer. You need not actually solve the equations.

Solution: The transition matrix is

$${\bf p} = \left[\begin{array}{cccc} p_A & 1-p_A & 0 & 0 \\ ... ... 0 & 0 & p_B &1-p_B \\ 1-p_B & 0 & p_B & 0 \end{array}\right]$$

The stationary probabilities $\pi_o,\pi_1\pi_2\pi_3$ satisfy $\pi=\pi{\bf p}$or
$$\begin{align*}\pi_0 &= \pi_0 p_A+\pi_1 p_A+\pi_3(1-p_B) \\ \pi_1 &= \pi_0 (1-p_... ...pi_3p_B \\ \pi_3 &= \pi_2 (1-p_B) \\ 1 = \pi_0+\pi_1+\pi_2+\pi_3 \end{align*}$$
The desired limiting frequency is $\pi_2+\pi_3$. For completeness the equations reduce to

$$1= \pi_2\frac{(1-p_b)^2}{(1-p_a)^2} + \pi_2 \frac{(1-p_b)^2}{(1-p_a)} + \pi_2 +\pi_2(1-p_B)$$

3.

A Markov Chain has state space $\{1,2,3,4\}$ and transition matrix

$$\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ \\ \frac{1}{3} &... ...{1}{2} & \frac{1}{4} \\ \\ 0 & 0 & 0 & 1 \end{array}\right]$$

(a)

Identify all the communicating classes and say whether or not each is transient.

Solution: The communicating classes are $\{1\}$ which is recurrent, $\{2,3\}$ which is transient and $\{4\}$ which is recurrent.

(b)

Let $q_k={\rm P}(\hbox{there is an $n$\space such that } X_n=4 \vert X_0=k)$. Derive the equations

$$q_2= (q_2+q_3)/3 \text{ and } q_3= (q_2+2q_3+1)/4$$

Solution: Notice that q₁=0 and q₄=1Split up over the 4 possible values of X₁. If X₁=1 then the conditional probability of ever reaching 4 is 0. If X₁=4 then the conditional probability of ever reaching 4 is 1; the probability that this happens starting from 2 is 0 and from 3 the probability that X₁=4 is 1/4. This gives

q₂ = P_2,1q₁+P_2,2q₂+P_2,3 q₃+P_2,4q₄

which simplifies to

$$q_2 = 0+\frac{1}{3} q_2+\frac{1}{3} q_3$$

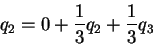
Similarly

q₃ = P_3,1q₁+P_3,2q₂+P_3,3 q₃+P_3,4q₄

which simplifies to

$$q_3 = 0+\frac{1}{4} q_2+\frac{2}{4} q_3 + \frac{1}{4} 1$$

Not required but the solution is q_i=(i-1)/3 for i=1,2,3,4.

4.

Cosmic rays are detected by a particle detector according to a Poisson Process with rate 2. An arriving cosmic ray is detected with probability 0.8 independent of all other cosmic rays and the time at which the cosmic ray arrives. Compute the probability that 4 cosmic rays arrived in a time period of length t=5 starting from time t=0 given that given that 8 cosmic rays were detected in the time period from t=0 to t=8.

Solution: Let U be the number arriving at detected in [0,5], V the number arriving and detected in (5,8], W the number arriving but undetected in [0,5], and X the number arriving but undetected in (5,8]. Then
$$\begin{align*}P(U=u,& V=v, W=w, X=x) \\ & = P(U=u\vert U+W=u+w)P(U+W=u+w) \\ &... ...(3p\lambda)^v}{v!} \frac{e^{-3(1-p)\lambda} (3(1-p)\lambda)^x}{x!} \end{align*}$$
We want

$$P(U+W=4\vert U+V=8) = \frac{P(U+W=4,U+V=8)}{P(U+V=8)}$$

The numerator is
$$\begin{multline*}\sum_{u=0}^4 P(U=j,W=4-j,V=8-j) \\ =\sum_{u=0}^4\frac{e^{-5p\... ...^{4-j}}{(4-j)!} \frac{e^{-3p\lambda} (3p\lambda)^{8-j}}{(8-j)!} \end{multline*}$$

The denominator is

$$\sum_{u=0}^8 \frac{e^{-5p\lambda} (5p\lambda)^u}{u!} \frac{e^{-3p\lambda} (3p\lambda)^{8-u}}{(8-u)!}$$

These pieces can be assembled and a numerical answer produced using $\lambda=2$ and p=0.8.