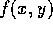STAT 801

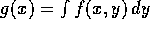Problems: Assignment 2

Suppose X and Y have joint density 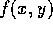. Prove from the definition of density that the density of X is .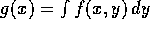

Suppose X is Poisson(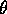). After observing X a coin landing Heads with probability p is tossed X times. Let Y be the number of Heads and Z be the number of Tails. Find the joint and marginal distributions of Y and Z.

Let 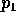be the bivariate normal density with mean 0, unit variances and correlation 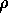and let 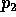be the standard bivariate normal density. Let .

1. Show that p has normal margins but is not bivariate normal.

2. Generaliz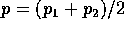e the construction to show that there rv's X and Y such that X and Y are each standard normal, X and Y are uncorrelated but X and Y are not independent.

Warning: This is probably hard. Don't waste too much time on it. Suppose X and Y are independent 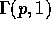and 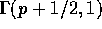random variables. Show that 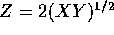is a 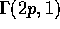random variable.

Suppose X and Y are independent with 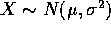and 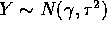. Let Z=X+Y. Find the distribution of Z given X and that of X given Z.

• About this document ...