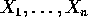 are iid real random variables with
density f . Let
are iid real random variables with
density f . Let 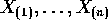 be the X 's arranged
in increasing order.
be the X 's arranged
in increasing order.
Problems: Assignment 3
Suppose 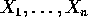 are iid real random variables with
density f . Let
are iid real random variables with
density f . Let 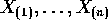 be the X 's arranged
in increasing order.
be the X 's arranged
in increasing order.
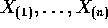 .
.
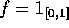 . Prove that
. Prove that 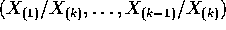 is independent of
is independent of 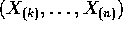 .
.
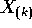 .
.
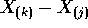 .
.
Suppose 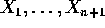 are iid exponential. Let
are iid exponential. Let 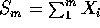 .
.
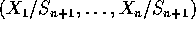 .
.
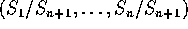 .
.
Suppose 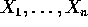 are iid N(
are iid N(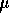 ,
,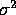 ).
Let
).
Let 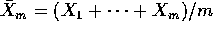 . Let
. Let 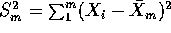 .
.
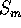 and
and 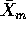 , expressing
, expressing
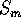 and
and 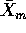 in terms of
in terms of 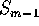 and
and 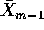 .
.
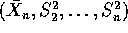 .
.
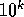 to the data for
some large values of k compare the numerical performance of these
recurrence relations to that of the one pass formula using
to the data for
some large values of k compare the numerical performance of these
recurrence relations to that of the one pass formula using
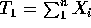 ,
, 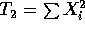 and the usual computing formulas
for the sample variance.
and the usual computing formulas
for the sample variance.
Suppose X and Y are iid 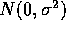 .
.
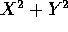 and
and 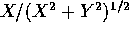 are independent.
are independent.
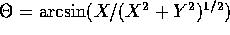 is uniformly
distributed on
is uniformly
distributed on 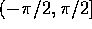 .
.
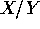 is a Cauchy random variable.
is a Cauchy random variable.