Postscript version of this file
STAT 450
Linear Algebra Review Notes
Notation:
- Vectors
 are column vectors
are column vectors
- An
 matrix A has m rows, n columns and entries
Aij.
matrix A has m rows, n columns and entries
Aij.
- Matrix and vector addition are defined componentwise:
- If A is
 and B is
and B is
 then AB is the
then AB is the
 matrix
matrix
- The matrix I or sometimes
 which is an
which is an
 matrix with
Iii = 1 for all i and Iij=0 for any pair
matrix with
Iii = 1 for all i and Iij=0 for any pair
 is called the
is called the  identity matrix.
identity matrix.
- The span of a set of vectors
 is the
set of all vectors x of the form
is the
set of all vectors x of the form
 .
It is a vector space.
The column space of a matrix, A, is the span of the set of columns
of A. The row space is the span of the set of rows.
.
It is a vector space.
The column space of a matrix, A, is the span of the set of columns
of A. The row space is the span of the set of rows.
- A set of vectors
 is linearly independent
if
is linearly independent
if
 implies ci=0 for all i. The dimension
of a vector space is the cardinality of the largest possible set of
linearly independent vectors.
implies ci=0 for all i. The dimension
of a vector space is the cardinality of the largest possible set of
linearly independent vectors.
Definition: The transpose, AT, of an  matrix A is
the
matrix A is
the
 matrix whose entries are given by
matrix whose entries are given by
(AT)ij = Aji
so that AT is
 .
We have
.
We have
(A+B)T = AT+BT
and
Definition: The rank of a matrix A is the number of linear independent
columns of A; we use
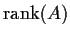 for notation.
We have
for notation.
We have

If A is
 then
then
 .
.
Matrix inverses
For this little section all matrices are square
 matrices.
matrices.
If there is a matrix B such that
 then
we call B the inverse of A. If B exists it is unique and
AB=I and we write B=A-1. The matrix A has an inverse if and only
if
then
we call B the inverse of A. If B exists it is unique and
AB=I and we write B=A-1. The matrix A has an inverse if and only
if
 .
.
Inverses have the following properties:
(AB)-1 = B-1A-1
(if one side exists then so does the other)
and
(AT)-1 = (A-1)T
Determinants
Again A is  .
The determinant if a function on the set
of
.
The determinant if a function on the set
of
 matrices such that:
matrices such that:
- 1.
-
 .
.
- 2.
- If
 is the matrix A with two columns interchanged
then
is the matrix A with two columns interchanged
then
(Notice that this means
that two equal columns guarantees
 .)
.)
- 3.
-
 is a linear function of each column of A.
That is if
is a linear function of each column of A.
That is if
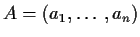 with ai denoting the ith
column of the matrix then
with ai denoting the ith
column of the matrix then

Here are some properties of the determinant:
- 4.
-
 .
.
- 5.
-
 .
.
- 6.
-
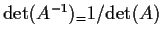 .
.
- 7.
- A is invertible if and only if
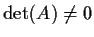 if and only if
if and only if
 .
.
- 8.
- Determinants can be computed (slowly) by expansion by minors.
Special Kinds of Matrices
- 1.
- A is symmetric if AT=A.
- 2.
- A is orthogonal if
AT=A-1 (or
AAT = ATA=I).
- 3.
- A is idempotent if
 .
.
- 4.
- A is diagonal if
 implies Aij=0.
implies Aij=0.
Inner Products and orthogonal and orthonormal vectors
Definition: Two vectors x and y are orthogonal if
 .
.
Definition: The inner product or dot product of x and y is
Definition: x and y are orthogonal if xTy=0.
Definition: The norm (or length) of x is
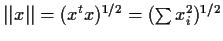
A is orthogonal if each column of A has length 1 and
is orthogonal to each other column of A.
Quadratic Forms
Suppose A is an
 matirx. The function
matirx. The function
g(x) = xT A x
is called a quadratic form. Now

so that g(x) depends only on the total
Aij+Aji. In
fact
Thus we will assume that A is symmetric.
Eigenvalues and eigenvectors
If A is
 and
and
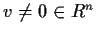 and
and
 are
such that
are
such that
then we saythat  is an eigenvalue (or characteristic
value or latent value) of A and that v is the corresponding
eigenvector. Since
is an eigenvalue (or characteristic
value or latent value) of A and that v is the corresponding
eigenvector. Since
 we find
that
we find
that
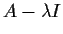 must be singular. Therefore
must be singular. Therefore
 .
Conversely if
.
Conversely if
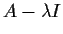 is singular
then there is a
is singular
then there is a  such that
such that
 .
In fact,
.
In fact,
 is a polynomial function of
is a polynomial function of  of degree
n. Each root is an eigenvalue. For general A the roots could be
multiple roots or complex valued.
of degree
n. Each root is an eigenvalue. For general A the roots could be
multiple roots or complex valued.
Diagonalization
A matrix A is diagonalized by a non-singular matrix
P is
 is a diagonal matrix. If so
then AP=PD and each column of P is an eignevector of A with
the ith column having eigenvlaue Dii. Thus to be diagonalizable
A must have n linearly independent eigenvectors.
is a diagonal matrix. If so
then AP=PD and each column of P is an eignevector of A with
the ith column having eigenvlaue Dii. Thus to be diagonalizable
A must have n linearly independent eigenvectors.
Symmetric Matrices
If A is symmetric then
- 1.
- Every eigenvalue of A is real (not complex).
- 2.
- A is diagonalizable and the columns of P may
be taken to be orthogonal to each other and of unit length.
In other words, A is diagonalizable by an orthogonal matrix
P; in symbols PTAP = D. The diagonal entries in D are the
eigenvalues of A.
- 3.
- If
 are two eigenvalues of Aand v1 and v2 are corresponding eigenvectors then
are two eigenvalues of Aand v1 and v2 are corresponding eigenvectors then
and

Since
 and
and
 we see that
v1T v2 = 0. In other words eigenvectors corresponding
to distinct eigenvalues are orthogonal.
we see that
v1T v2 = 0. In other words eigenvectors corresponding
to distinct eigenvalues are orthogonal.
Orthogonal Projections
Suppose that S is a vector subspace of Rn and that
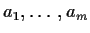 are a basis for S. Given any
are a basis for S. Given any  there
is a unique
there
is a unique 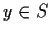 which is closest to x. That is, y minimizes
which is closest to x. That is, y minimizes
(x-y)T(X-y)
over 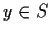 .
Any y in S is of the form
.
Any y in S is of the form
where A is the
 matrix with columns
matrix with columns
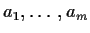 and
c is the column vector with ith entry ci. Define
and
c is the column vector with ith entry ci. Define
Q= A(ATA)-1AT
(The fact that A has rank m guarantees that ATA is invertible.)
Then

Note that
x-Qx = (I-Q)x and that
QAc = A(ATA)-1ATAc = Ac
so that
Qx-Ac = Q(x-Ac)
Then
(Qx-Ac)T(x-Qx) = (x-Ac)T QT (I-Q) x
Since QT=Q we see that

This shows that
(x-Ac)T(x-Ac) = (x-Qx)T(x-Qx) + (Qx-Ac)T(Qx-Ac)
Now to choose Ac to minimize this quantity we need only
minimize the second term. This is achieved by making
Qx=Ac. Since
Qx=A(ATA)-1AT x this can be done
by taking
c=(ATA)-1AT x. In summary we find that the
closest point y in S is
y=Qx=A(ATA)-1AT x
We call y the orthogonal projection of x onto S.
Notice that the matrix Q is idempotent:
Q2=Q
We call Qx the orthogonal projection of x on S because
Qx is perpendicular to the residual
x-Qx=(I-Q)x.
Partitioned Matrices
Suppose that A11 is a
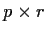 matrix, A1,2 is
matrix, A1,2 is
 ,
A2,1 is
,
A2,1 is
 and A2,2 is
and A2,2 is
 .
Then we could make a big
.
Then we could make a big
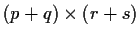 matrix
by putting together the Aij in a 2 by 2 matrix giving the following
picture:
matrix
by putting together the Aij in a 2 by 2 matrix giving the following
picture:
For instance if
and
then
where I have drawn in lines to indicate the partitioning.
We can work with partitioned matrices just like ordinary matrices
always making sure that in products we never change the order of
multiplication of things.
and
In these formulas the partitioning of A and B must match.
For the addition formula the dimensions of Aij and Bijmust be the same. For the multiplication formula A12 must
have as many columns as B21 has rows and so on. In general
Aij and Bjk must be of the right size for
AijBjkto make sense for each i,j,k.
The technique can be used with more than a 2 by 2 partitioning.
Definition: A block diagonal matrix is a partitioned matrix Awith pieces Aij for which Aij=0 if  .
If
.
If
then A is invertible if and only if each Aii is invertible and
then
Moreover
 .
Similar formulas work for larger matrices.
.
Similar formulas work for larger matrices.
Richard Lockhart
1999-09-23
![\begin{displaymath}x=\left[\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right]
\end{displaymath}](img2.gif)

![\begin{displaymath}x=\left[\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right]
\end{displaymath}](img2.gif)

![]() matrix A is
the
matrix A is
the
![]() matrix whose entries are given by
matrix whose entries are given by
![]() for notation.
We have
for notation.
We have

![]() then
then
![]() .
.
![]() matrices.
matrices.
![]() then
we call B the inverse of A. If B exists it is unique and
AB=I and we write B=A-1. The matrix A has an inverse if and only
if
then
we call B the inverse of A. If B exists it is unique and
AB=I and we write B=A-1. The matrix A has an inverse if and only
if
![]() .
.
![]() .
The determinant if a function on the set
of
.
The determinant if a function on the set
of
![]() matrices such that:
matrices such that:
![]() .
.
![]()
![]() matirx. The function
matirx. The function


![]() and
and
![]() and
and
![]() are
such that
are
such that
![]() is a diagonal matrix. If so
then AP=PD and each column of P is an eignevector of A with
the ith column having eigenvlaue Dii. Thus to be diagonalizable
A must have n linearly independent eigenvectors.
is a diagonal matrix. If so
then AP=PD and each column of P is an eignevector of A with
the ith column having eigenvlaue Dii. Thus to be diagonalizable
A must have n linearly independent eigenvectors.

![]() are a basis for S. Given any
are a basis for S. Given any ![]() there
is a unique
there
is a unique ![]() which is closest to x. That is, y minimizes
which is closest to x. That is, y minimizes


![]() matrix, A1,2 is
matrix, A1,2 is
![]() ,
A2,1 is
,
A2,1 is
![]() and A2,2 is
and A2,2 is
![]() .
Then we could make a big
.
Then we could make a big
![]() matrix
by putting together the Aij in a 2 by 2 matrix giving the following
picture:
matrix
by putting together the Aij in a 2 by 2 matrix giving the following
picture:
![\begin{displaymath}A = \left[ \begin{array}{cc}
A_{11} & A_{12}
\\
A_{21} & A_{22}
\end{array}\right]
\end{displaymath}](img64.gif)
![\begin{displaymath}A_{11} = \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]
\end{displaymath}](img65.gif)
![\begin{displaymath}A_{12} = \left[ \begin{array}{c} 2 \\ 3 \end{array}\right]
\end{displaymath}](img66.gif)
![\begin{displaymath}A = \left[ \begin{array}{cc\vert c}
1 & 0 & 2
\\
0 & 1 & 3
\\
\hline
4 & 5 & 6
\end{array}\right]
\end{displaymath}](img69.gif)
![\begin{displaymath}\left[ \begin{array}{cc}
A_{11} & A_{12}
\\
A_{21} & A_{22}
...
...2}+B_{12}
\\
A_{21}+B_{21} & A_{22}+B_{22}
\end{array}\right]
\end{displaymath}](img70.gif)
![\begin{displaymath}\left[ \begin{array}{cc}
A_{11} & A_{12}
\\
A_{21} & A_{22}
...
...1}+A_{22}B_{21} &A_{21}B_{12}+ A_{22}B_{22}
\end{array}\right]
\end{displaymath}](img71.gif)
![]() .
If
.
If
![\begin{displaymath}A = \left[ \begin{array}{cc}
A_{11} & 0
\\
0 & A_{22}
\end{array}\right]
\end{displaymath}](img72.gif)
![\begin{displaymath}A^{-1} = \left[ \begin{array}{cc}
A_{11}^{-1} & 0
\\
0 & A_{22}^{-1}
\end{array}\right]
\end{displaymath}](img73.gif)