


Next: About this document
STAT 450
Problems: Assignment 1
These problems serve a variety of purposes. One is practice with the
ideas from class. Some problems provide counterexamples and illustrate the
regularity conditions of theorems. Some problems introduce, without much
explanation, ideas we won't have time to consider in class. The first 3 are
review intended to let me see how well you explain things you understand
and to make sure the basics are already there.
- The concentration of cadmium in a lake is measured 17 times. The
measurements average 211 parts per billion with an SD of 15 parts per
billion. Could the real concentration of cadmium be below the standard of
200 ppb?
- Consider a population of 200 million people of whom 200 thousand have a
certain condition. A test is available with the following properties.
Assuming that a person has the condition the probability that the test
detects the condition is 0.9. Assuming that a person does not have the
condition the test detects (incorrectly) the condition with probability 0.001.
A person is picked at random from the 200 million people and the test is
administered.
- What is the chance that the test detects the condition for this randomly
selected person?
- Assuming that the condition is detected by the test for this randomly
selected person what is the chance that the person has the condition?
- A mandatory testing program is contemplated. If all 200 million are
tested about how many positive results should be expected? Of these
about how many will not have the condition?
- Suppose X and Y are independent Geometric(p) random variables.
In other words
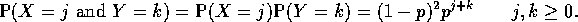
- Let
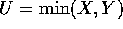 ,
, 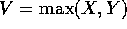 and W=V-U. Express the event
U=j and W=k in terms of X and Y.
and W=V-U. Express the event
U=j and W=k in terms of X and Y.
- Compute
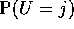 and
and 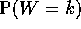 and prove that the event
U=j and the event W=k are independent.
and prove that the event
U=j and the event W=k are independent.
- A computer is waiting for two flags to be set. Both flags start
out not set.
For each flag the conditional probability that the flag is set next cycle
given it is not yet set is 0.5. The two flags operate independently. How
many cycles should you expect to wait before both flags are set including
the cycle on which the last flag becomes set?
- Question 27 on page 128.



Next: About this document
Richard Lockhart
Wed Oct 2 22:22:17 PDT 1996
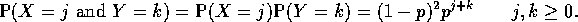
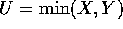 ,
, 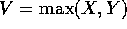 and W=V-U. Express the event
U=j and W=k in terms of X and Y.
and W=V-U. Express the event
U=j and W=k in terms of X and Y.
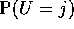 and
and 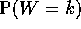 and prove that the event
U=j and the event W=k are independent.
and prove that the event
U=j and the event W=k are independent.