


Next: About this document
STAT 450
Problems: Assignment 2
Basic Questions
- Suppose
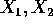 are iid real random variables with
density f . Let
are iid real random variables with
density f . Let 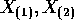 be the X 's arranged
in increasing order, that is,
be the X 's arranged
in increasing order, that is, 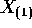 is the minimum of
is the minimum of 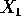 and
and 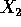 while
while 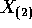 is the maximum.
is the maximum.
- Find the joint density of
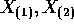 .
.
- Suppose
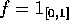 . Prove that
. Prove that 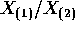 is independent of
is independent of 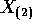 .
.
- Find the density of
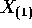 .
.
- Find the density of
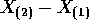 .
.
- Suppose
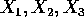 are iid exponential. Let
are iid exponential. Let 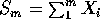 for i=1, 2 and 3.
for i=1, 2 and 3.
- Find the joint density of
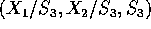 .
.
- Find the joint density of
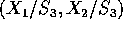 .
.
- Find the joint density of
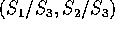 .
.
- Suppose X and Y have joint density
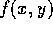 . Prove from the
definition of density that the density of X is
. Prove from the
definition of density that the density of X is 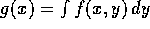 .
.
- Suppose X is Poisson(
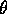 ). After observing X a coin landing
Heads with probability p is tossed X times. Let Y be the number of
Heads and Z be the number of Tails. Find the joint and marginal distributions
of Y and Z.
). After observing X a coin landing
Heads with probability p is tossed X times. Let Y be the number of
Heads and Z be the number of Tails. Find the joint and marginal distributions
of Y and Z.
- Let
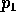 be the bivariate normal density with mean 0,
unit variances and correlation
be the bivariate normal density with mean 0,
unit variances and correlation 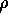 and let
and let 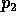 be the standard
bivariate normal density. Let
be the standard
bivariate normal density. Let 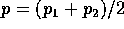 .
Show that p has normal margins but is not bivariate normal.
.
Show that p has normal margins but is not bivariate normal.
- Suppose X and Y are independent with
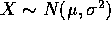 and
and 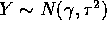 . Let Z=X+Y.
Find the distribution of Z given X and that of X given Z.
. Let Z=X+Y.
Find the distribution of Z given X and that of X given Z.
Richard Lockhart
Tue Oct 8 09:10:57 PDT 1996
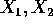 are iid real random variables with
density f . Let
are iid real random variables with
density f . Let 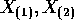 be the X 's arranged
in increasing order, that is,
be the X 's arranged
in increasing order, that is, 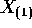 is the minimum of
is the minimum of 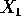 and
and 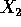 while
while 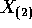 is the maximum.
is the maximum.
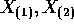 .
.
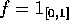 . Prove that
. Prove that 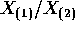 is independent of
is independent of 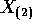 .
.
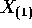 .
.
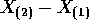 .
.
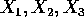 are iid exponential. Let
are iid exponential. Let 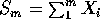 for i=1, 2 and 3.
for i=1, 2 and 3.
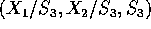 .
.
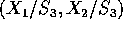 .
.
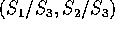 .
.
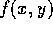 . Prove from the
definition of density that the density of X is
. Prove from the
definition of density that the density of X is 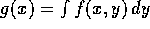 .
.
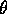 ). After observing X a coin landing
Heads with probability p is tossed X times. Let Y be the number of
Heads and Z be the number of Tails. Find the joint and marginal distributions
of Y and Z.
). After observing X a coin landing
Heads with probability p is tossed X times. Let Y be the number of
Heads and Z be the number of Tails. Find the joint and marginal distributions
of Y and Z.
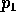 be the bivariate normal density with mean 0,
unit variances and correlation
be the bivariate normal density with mean 0,
unit variances and correlation 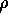 and let
and let 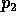 be the standard
bivariate normal density. Let
be the standard
bivariate normal density. Let 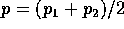 .
Show that p has normal margins but is not bivariate normal.
.
Show that p has normal margins but is not bivariate normal.
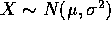 and
and 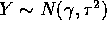 . Let Z=X+Y.
Find the distribution of Z given X and that of X given Z.
. Let Z=X+Y.
Find the distribution of Z given X and that of X given Z.