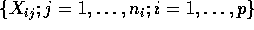 are independent
are independent
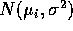 random variables. (This is the
usual set-up for the one-way layout.)
random variables. (This is the
usual set-up for the one-way layout.)
- Find the MLE's for
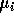 and
and 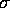 .
.
- Find the expectations and variances of these estimators.
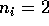 for all i and let
for all i and let 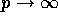 .
What happens to
the MLE of
.
What happens to
the MLE of 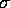 ?
Hint: you have calculated the mean and variance
of the MLE of
?
Hint: you have calculated the mean and variance
of the MLE of 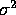 .
What are the limits of these quantities?
.
What are the limits of these quantities?
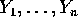 are independent random variables
and that
are independent random variables
and that  are
the corresponding values of some covariate.
Suppose that the density of
are
the corresponding values of some covariate.
Suppose that the density of 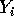 is
is

where  , and
, and 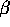 are unknown parameters.
Find the log-likelihood, the score function and the Fisher information.
are unknown parameters.
Find the log-likelihood, the score function and the Fisher information.
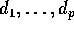 a number of animals
a number of animals 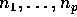 are treated with the corresponding dose of some drug. The
number dying at dose d is Binomial with parameter
are treated with the corresponding dose of some drug. The
number dying at dose d is Binomial with parameter 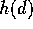 . A common model
for
. A common model
for 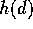 is
is 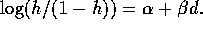
- Find the likelihood equations for estimating
 and
and 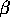 .
.
- Find the Fisher information matrix.