


Next: About this document
STAT 450
Problems: Assignment 6
- Page 365. Q 21.
- Page 365 Q 24.
- Page 366. Q 28.
- Page 366. Q 29.
- Suppose
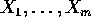 are iid
are iid 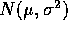 and
and
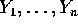 are iid
are iid  .
.
- Find complete and sufficient statistics.
- Find UMVUE's of
 and
and 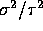 .
.
- Now suppose you know that
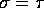 . Find UMVUE's of
. Find UMVUE's of
 and of
and of 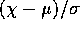 . (You have already found
the UMVUE for
. (You have already found
the UMVUE for 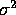 .)
.)
- Now suppose
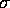 and
and  are unknown but that you
know that
are unknown but that you
know that 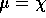 . Prove there is no UMVUE for
. Prove there is no UMVUE for 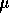 .
(Hint: Find the UMVUE if you knew
.
(Hint: Find the UMVUE if you knew 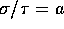 with a known.
Use the fact that the solution depends on a to finish the proof.)
with a known.
Use the fact that the solution depends on a to finish the proof.)
- Why doesn't the Lehmann-Scheffé theorem apply?
- Suppose
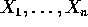 iid Poisson(
iid Poisson( 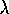 ). Find the
UMVUE for
). Find the
UMVUE for 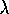 and for
and for 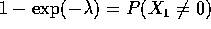 .
.
- Let
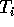 be the error sum of squares in the ith cell in the
question 5 of Assignment 5.
be the error sum of squares in the ith cell in the
question 5 of Assignment 5.
- Find the joint density of the
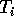 .
.
- Find the best estimate of
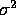 of the form
of the form 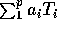 in the sense of mean squared error.
in the sense of mean squared error.
- Do the same under the condition that the estimator must be unbiased.
- If only
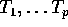 are observed what is the MLE of
are observed what is the MLE of 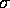 ?
?
- Find the UMVUE of
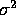 for the usual one-way layout model,
that is, the model of the last two questions.
for the usual one-way layout model,
that is, the model of the last two questions.
- Exponential families: Suppose
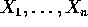 are iid with density
are iid with density
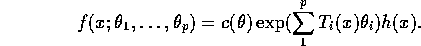
- Find minimal sufficient statistics.
- If
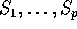 are the minimal sufficient statistics show
that setting
are the minimal sufficient statistics show
that setting 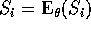 and solving gives the
likelihood equations. (Note the connection to the method of moments.)
and solving gives the
likelihood equations. (Note the connection to the method of moments.)
Richard Lockhart
Sun Oct 27 19:00:53 PST 1996
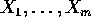 are iid
are iid 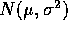 and
and
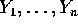 are iid
are iid  .
.
 and
and 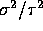 .
.
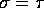 . Find UMVUE's of
. Find UMVUE's of
 and of
and of 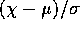 . (You have already found
the UMVUE for
. (You have already found
the UMVUE for 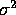 .)
.)
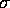 and
and  are unknown but that you
know that
are unknown but that you
know that 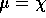 . Prove there is no UMVUE for
. Prove there is no UMVUE for 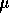 .
(Hint: Find the UMVUE if you knew
.
(Hint: Find the UMVUE if you knew 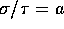 with a known.
Use the fact that the solution depends on a to finish the proof.)
with a known.
Use the fact that the solution depends on a to finish the proof.)
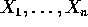 iid Poisson(
iid Poisson( 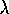 ). Find the
UMVUE for
). Find the
UMVUE for 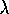 and for
and for 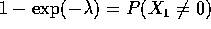 .
.
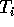 be the error sum of squares in the ith cell in the
question 5 of Assignment 5.
be the error sum of squares in the ith cell in the
question 5 of Assignment 5.
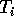 .
.
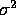 of the form
of the form 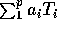 in the sense of mean squared error.
in the sense of mean squared error.
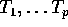 are observed what is the MLE of
are observed what is the MLE of 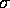 ?
?
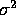 for the usual one-way layout model,
that is, the model of the last two questions.
for the usual one-way layout model,
that is, the model of the last two questions.
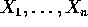 are iid with density
are iid with density
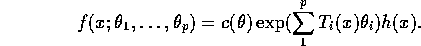
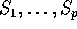 are the minimal sufficient statistics show
that setting
are the minimal sufficient statistics show
that setting 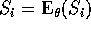 and solving gives the
likelihood equations. (Note the connection to the method of moments.)
and solving gives the
likelihood equations. (Note the connection to the method of moments.)