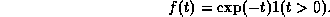
- Find the density of
 .
.
- Suppose a test statistic has the distribution of T. Derive a
formula for the upper
 critical point of the test statistic.
critical point of the test statistic.
 has a multivariate normal distribution with
mean vector
has a multivariate normal distribution with
mean vector  and variance covariance matrix
and variance covariance matrix
 where
where  is a known diagonal
matrix.
is a known diagonal
matrix.
- Give a general formula for the log-likelihood
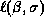 . Your answer should be written in matrix form.
. Your answer should be written in matrix form.
- Let
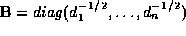 . Let
. Let  . What is the distribution of
. What is the distribution of  ? Show that
? Show that  satisfies a linear model and identify the design matrix
satisfies a linear model and identify the design matrix 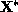 for this
linear model.
for this
linear model.
- For the special case
 and
and

derive the likelihood equations.
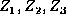 are independent standard normal
variables. What is the distribution of
are independent standard normal
variables. What is the distribution of
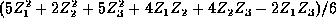 ?
?
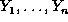 are independent random variables
and that
are independent random variables
and that 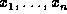 are the corresponding values of some covariate.
Suppose that the density of
are the corresponding values of some covariate.
Suppose that the density of 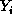 is
is 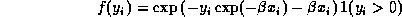
where 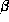 is an unknown parameter. Find
the log-likelihood, the score function and the Fisher information. You may
use without proof the fact that
is an unknown parameter. Find
the log-likelihood, the score function and the Fisher information. You may
use without proof the fact that 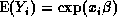 .
.
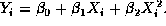 Fitting this model by least squares, the error sum of squares is 2.231177.
For the model
Fitting this model by least squares, the error sum of squares is 2.231177.
For the model 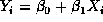 the error sum of squares is
2.59839. For the model
the error sum of squares is
2.59839. For the model 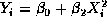 the error sum of
squares is 2.641787. For the model
the error sum of
squares is 2.641787. For the model  the error sum of
squares is 3.144104. There are 20 data points.
the error sum of
squares is 3.144104. There are 20 data points.
- Test the hypothesis that
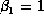 and
and  using
this information.
using
this information.
- Now consider the model
 .
Let
.
Let  be the error sum of squares when this model is fitted
by least squares. Let
be the error sum of squares when this model is fitted
by least squares. Let  be the corresponding least squares
estimates. Show that the MLE of
be the corresponding least squares
estimates. Show that the MLE of  is
is 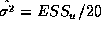 and evaluate the log-likelihood,
and evaluate the log-likelihood,  . (The answer is a number which can be calculated from the
information given in this question.)
. (The answer is a number which can be calculated from the
information given in this question.)
- Use the idea in b) to calculate the profile likelihood
 which is the maximum of the log
likelihood for the model
which is the maximum of the log
likelihood for the model 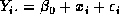 .
.
- Now compute a P-value for the likelihood ratio test statistic
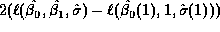 .
.
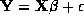 is
fitted. It is found that
is
fitted. It is found that 
and that

There are 23 data points. The error sum of squares is 80.
- Give a 90% confidence interval for
 .
.
- Test the hypothesis that
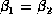 .
.
- A new observation is planned; the row in the design matrix
for this new observation would be 1,-1,2. Give a 95% prediction interval for
the new Y.
- Assume that in fact
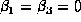 . What is the
distribution of
. What is the
distribution of 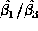 ?
?