

Postscript version of this page
STAT 801: Mathematical Statistics
Hypothesis Testing and Decision Theory
Decision analysis of hypothesis testing takes
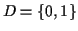 and
and
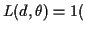
make an error
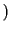
or more generally
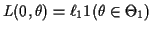 and
and
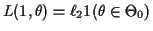 for two positive
constants
for two positive
constants 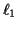 and
and 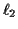 . We make the decision space convex
by allowing a decision to be a probability measure on
. We make the decision space convex
by allowing a decision to be a probability measure on 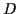 . Any such measure
can be specified by
. Any such measure
can be specified by
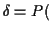 reject
reject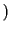 so
so
![$ {\cal D} =[0,1]$](img11.gif) . The
loss function of
. The
loss function of
![$ \delta\in[0,1]$](img12.gif) is
is
Simple hypotheses: Prior is 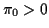 and
and 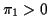 with
with
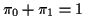 .
.
Procedure: map from sample space to 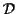 - a test function.
- a test function.
Risk function of procedure 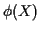 is a pair of numbers:
is a pair of numbers:
and
We find
and
The Bayes risk of 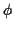 is
We saw in the hypothesis testing section that this is minimized
by
which is a likelihood ratio test. These tests are Bayes
and admissible. The risk is constant if
is
We saw in the hypothesis testing section that this is minimized
by
which is a likelihood ratio test. These tests are Bayes
and admissible. The risk is constant if
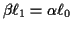 ;
you can use this to find the minimax test in this context.
;
you can use this to find the minimax test in this context.


Richard Lockhart
2001-01-03
![]() and
and
![]() and
and ![]() with
with
![]() .
.
![]() - a test function.
- a test function.
![]() is a pair of numbers:
is a pair of numbers: