


Postscript version of this file
STAT 801 Lecture 15
Reading for Today's Lecture:
Goals of Today's Lecture:
- Define MSE and unbiasedness.
- Define UMVUEs.
- Introduce Cramér Rao Lower Bound
Today's notes
Finding (good) preliminary Point Estimates
Method of Moments
Basic strategy: set sample moments equal to population moments and
solve for the parameters.
Gamma Example
The Gamma(
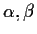 )
density is
)
density is
and has
and
This gives the equations

or

Divide the second equation by the first to find
the method of moments estimate of  is
is
Then from the first equation get
These equations are much easier to solve than the likelihood equations. The
latter
involve the function
called the digamma function. The score function in this problem has
components
and
You can solve for  in terms of
in terms of  to leave you
trying to find a root of the equation
to leave you
trying to find a root of the equation
To use Newton Raphson on this you begin with the preliminary
estimate
 and then compute iteratively
and then compute iteratively
until the sequence converges. Computation of
 ,
the
trigamma function, requires special software. Web sites like netlib
and statlib are good sources for this sort of thing.
,
the
trigamma function, requires special software. Web sites like netlib
and statlib are good sources for this sort of thing.
Optimality theory for point estimates
Why bother doing the Newton Raphson steps? Why not just use
the method of moments estimates? The answer is that the
method of moments estimates are not usually as close to
the right answer as the mles.
Rough principle: A good estimate
 of
of  is usually
close to
is usually
close to  if
if  is the true value of
is the true value of  .
Closer
estimates, more often, are better estimates.
.
Closer
estimates, more often, are better estimates.
This principle must be quantified if we are to ``prove'' that the mle is
a good estimate. In the Neyman Pearson spirit we measure average closeness.
Definition: The Mean Squared Error (MSE) of an estimator
 is the function
is the function
Standard identity:
where the bias is defined as
Primitive example: I take a coin from my pocket and toss it
6 times. I get HTHTTT. The MLE of the probability of heads is
where X is the number of heads. In this case I get
 .
.
An alternative estimate is
 .
That is,
.
That is,
 ignores the data and guesses the coin is fair. The
MSEs of these two estimators are
ignores the data and guesses the coin is fair. The
MSEs of these two estimators are
and
MSE0.5 = (p-0.5)2
If p is between 0.311 and 0.689 then the second MSE is smaller
than the first. For this reason I would recommend use of  for sample sizes this small.
for sample sizes this small.
Now suppose I did the same experiment with a thumbtack. The tack
can land point up (U) or tipped over (O). If I get
UOUOOO how should I estimate p the probability of U? The
mathematics is identical to the above but it seems clear that
there is less reason to think  is better than
is better than  since there is less reaon to believe
since there is less reaon to believe
 than
with a coin.
than
with a coin.
Unbiased Estimation
The problem above illustrates a general phenomenon. An estimator can
be good for sme values of  and bad for others. When comparing
and bad for others. When comparing
 and
and
 ,
two estimators of
,
two estimators of  we will say
that
we will say
that
 is better than
is better than
 if it has uniformly
smaller MSE:
if it has uniformly
smaller MSE:
for all  .
Normally we also require that the inequality
be strict for at least one
.
Normally we also require that the inequality
be strict for at least one  .
.
The definition raises the question of the existence of a best
estimate - one which is better than every other estimator. There is
no such estimate. Suppose
 were such a best estimate. Fix
a
were such a best estimate. Fix
a  in
in  and let
and let
 .
Then the
MSE of
.
Then the
MSE of  is 0 when
is 0 when
 .
Since
.
Since
 is
better than
is
better than  we must have
we must have
so that
 with probability equal to 1. This makes
with probability equal to 1. This makes
 .
If there are actually two different possible
values of
.
If there are actually two different possible
values of  this gives a contradiction; so no such
this gives a contradiction; so no such
 exists.
exists.
Principle of Unbiasedness: A good estimate is unbiased, that is,
WARNING: In my view the Principle of Unbaisedness is a load of hog wash.
For an unbiased estimate the MSE is just the variance.
Definition: An estimator  of a parameter
of a parameter
 is
Uniformly Minimum Variance Unbiased (UMVU) if, whenever
is
Uniformly Minimum Variance Unbiased (UMVU) if, whenever
 is an unbiased estimate of
is an unbiased estimate of  we have
we have
We call  the UMVUE. (`E' is for Estimator.)
the UMVUE. (`E' is for Estimator.)
The point of having
 is to study problems like estimating
is to study problems like estimating
 when you have two parameters like
when you have two parameters like  and
and  for example.
for example.
Cramér Rao Inequality
If
 we can derive some informtion from the
identity
we can derive some informtion from the
identity
When we worked with the score function we derived some information
from the identity
by differentiation and we do the same here. If T=T(X) is some function
of the data X which is unbiased for  then
then
Differentiate both sides to get

where U is the score function. Since we already know that the score has
mean 0 we see that
Now remember that correlations are between -1 and 1 or
Squaring gives the inequality
which is called the Cramér Rao Lower Bound. The inequality is
strict unless the correlation is 1 which would require that
for some non-random constants A and B (which might depend on  .)
This would prove that
.)
This would prove that
for some further constants A* and B* and finally
for h=eC.
Summary of Implications
- You can recognize a UMVUE sometimes. If
 then T(X) is the UMVUE. For instance in the
then T(X) is the UMVUE. For instance in the
 example the Fisher information is n and
example the Fisher information is n and
 so that
so that
 is the UMVUE of
is the UMVUE of  .
.
- In an asymptotic sense the MLE is nearly optimal: it is nearly
unbiased and (approximate) variance nearly
 .
.
- Good estimates are highly correlated with the score function.
- Densities of the exponential form given above are somehow special.
(The form is called an exponential family.)
- For most problems the inequality will be strict. It is strict unless
The score is an affine function of a statistic T and T (possibility
divided by some constant which doesn't depend on
 )
is unbiased for
)
is unbiased for
 .
.
What can we do to find UMVUEs when the CRLB is a strict inequality?
Example: Suppose X has a Binomial(n,p) distribution.
The score function is
Thus the CRLB will be strict unless T=cX for some c. If we are trying
to estimate p then choosing c=n-1 does give an unbiased estimate
 and T=X/n achieves the CRLB so it is UMVU.
and T=X/n achieves the CRLB so it is UMVU.
A different tactic proceeds as follows. Suppose
T(X) is some unbiased function of X. Then we have
because
 is also unbiased. If
h(k) = T(k)-k/n then
is also unbiased. If
h(k) = T(k)-k/n then
The left hand side of the  sign is a polynomial function of p
as is the right. Thus if the left hand side is expanded out the
coefficient of each power pk is 0. The constant term
occurs only in the term k=0 and its coefficient is
sign is a polynomial function of p
as is the right. Thus if the left hand side is expanded out the
coefficient of each power pk is 0. The constant term
occurs only in the term k=0 and its coefficient is
Thus h(0) = 0. Now p1=p occurs only in the term k=1 with
coefficient nh(1) so h(1)=0. Since the terms with k=0 or 1 are
0 the quantity p2 occurs only in the term with k=2 with coefficient
n(n-1)h(2)/2
so h(2)=0. We can continue in this way to see that in fact h(k)=0 for
each k and so the only unbiased function of X is X/n.
Now a Binomial random variable is just of sum of n iid Bernouilli(p)
random variables. If
 are iid Bernouilli(p) then
are iid Bernouilli(p) then
 is Binomial(n,p). Could we do better by than
is Binomial(n,p). Could we do better by than
 by trying
by trying
 for some other function T?
for some other function T?
Let's consider the case n=2 so that there are 4 possible values for
Y1,Y2. If
h(Y1,Y2) = T(Y1,Y2) - [Y1+Y2]/2 then again
and we have
Ep( h(Y1,Y2)) = h(0,0)(1-p)2 +
[h(1,0)+h(0,1)]p(1-p)+ h(1,1) p2
This can be rewritten in the form
where
w(0)=h(0,0),
w(1) =[h(1,0)+h(0,1)]/2 and
w(2) = h(1,1). Just
as before it follows that
w(0)=w(1)=w(2)=0. This argument can be used to
prove that for any unbiased estimate
 we have that the
average value of
we have that the
average value of
 over vectors
over vectors
 which
have exactly k 1s and n-k 0s is k/n. Now let's look at the variance
of T:
which
have exactly k 1s and n-k 0s is k/n. Now let's look at the variance
of T:
![\begin{align*}{\rm Var(T)} = & E_p( [T(Y_1,\ldots,Y_n) - p]^2)
\\
=& E_p( [T(...
...
& + 2E_p( [T(Y_1,\ldots,Y_n)
-X/n][X/n-p])
\\ & + E_p([X/n-p]^2)
\end{align*}](img79.gif)
I claim that the cross product term is 0 which will prove that the variance
of T is the variance of X/n plus a non-negative quantity (which will
be positive unless
 ).
We can compute the cross product term by writing
).
We can compute the cross product term by writing
![\begin{multline*}E_p( [T(Y_1,\ldots,Y_n)-X/n][X/n-p])
\\ \sum_{y_1,\ldots,y_n}
...
...,y_n)-\sum y_i/n][\sum y_i/n -p] p^{\sum y_i} (1-p)^{n-\sum
y_i}
\end{multline*}](img81.gif)
We can do the sum by summing over those
 whose sum is an
integer x and then summing over x. We get
whose sum is an
integer x and then summing over x. We get
![\begin{multline*}E_p( [T(Y_1,\ldots,Y_n)-X/n][X/n-p])
\\
= \sum_{x=0}^n
\sum...
...m y_i=x} [T(y_1,\ldots,y_n)-x/n]\right][x/n -p]p^{x}
(1-p)^{n-x}
\end{multline*}](img82.gif)
We have already shown that the sum in [] is 0!
This long, algebraically involved, method of proving that
 is the UMVUE of p is one special case of
a general tactic.
is the UMVUE of p is one special case of
a general tactic.
To get more insight I begin by rewriting

Notice that the large fraction in this formula is the average value
of T over values of y when  is held fixed at x. Notice
that the weights in this average do not depend on p. Notice that
this average is actually
is held fixed at x. Notice
that the weights in this average do not depend on p. Notice that
this average is actually

Notice that the conditional probabilities do not depend on p. In a
sequence of Binomial trials if I tell you that 5 of 17 were heads and the
rest tails the actual trial numbers of the 5 Heads are chosen at random
from the 17 possibilities; all of the 17 choose 5 possibilities have the
same chance and thsi chance does not depend on p.
Notice that in this problem with data
 the log likelihood
is
the log likelihood
is
and
as before. Again we see that the CRLB will be a strict inequality except
for multiples of X. Since the only unbiased multiple of X is
 we see again that
we see again that  is UMVUE for p.
is UMVUE for p.



Richard Lockhart
1998-10-29
![]() )
density is
)
density is
![\begin{displaymath}f(x;\alpha,\beta) =
\frac{1}{\beta\Gamma(\alpha)}\left(\frac{...
...ta}\right)^{\alpha-1}
\exp\left[-\frac{x}{\beta}\right] 1(x>0)
\end{displaymath}](img3.gif)




![]() of
of ![]() is usually
close to
is usually
close to ![]() if
if ![]() is the true value of
is the true value of ![]() .
Closer
estimates, more often, are better estimates.
.
Closer
estimates, more often, are better estimates.
![]() is the function
is the function
![]() .
That is,
.
That is,
![]() ignores the data and guesses the coin is fair. The
MSEs of these two estimators are
ignores the data and guesses the coin is fair. The
MSEs of these two estimators are
![]() is better than
is better than ![]() since there is less reaon to believe
since there is less reaon to believe
![]() than
with a coin.
than
with a coin.
![]() and bad for others. When comparing
and bad for others. When comparing
![]() and
and
![]() ,
two estimators of
,
two estimators of ![]() we will say
that
we will say
that
![]() is better than
is better than
![]() if it has uniformly
smaller MSE:
if it has uniformly
smaller MSE:
![]() were such a best estimate. Fix
a
were such a best estimate. Fix
a ![]() in
in ![]() and let
and let
![]() .
Then the
MSE of
.
Then the
MSE of ![]() is 0 when
is 0 when
![]() .
Since
.
Since
![]() is
better than
is
better than ![]() we must have
we must have
![]() of a parameter
of a parameter
![]() is
Uniformly Minimum Variance Unbiased (UMVU) if, whenever
is
Uniformly Minimum Variance Unbiased (UMVU) if, whenever
![]() is an unbiased estimate of
is an unbiased estimate of ![]() we have
we have
![]() is to study problems like estimating
is to study problems like estimating
![]() when you have two parameters like
when you have two parameters like ![]() and
and ![]() for example.
for example.
![]() we can derive some informtion from the
identity
we can derive some informtion from the
identity





![]() are iid Bernouilli(p) then
are iid Bernouilli(p) then
![]() is Binomial(n,p). Could we do better by than
is Binomial(n,p). Could we do better by than
![]() by trying
by trying
![]() for some other function T?
for some other function T?

![\begin{align*}{\rm Var(T)} = & E_p( [T(Y_1,\ldots,Y_n) - p]^2)
\\
=& E_p( [T(...
...
& + 2E_p( [T(Y_1,\ldots,Y_n)
-X/n][X/n-p])
\\ & + E_p([X/n-p]^2)
\end{align*}](img79.gif)
![\begin{multline*}E_p( [T(Y_1,\ldots,Y_n)-X/n][X/n-p])
\\ \sum_{y_1,\ldots,y_n}
...
...,y_n)-\sum y_i/n][\sum y_i/n -p] p^{\sum y_i} (1-p)^{n-\sum
y_i}
\end{multline*}](img81.gif)
![\begin{multline*}E_p( [T(Y_1,\ldots,Y_n)-X/n][X/n-p])
\\
= \sum_{x=0}^n
\sum...
...m y_i=x} [T(y_1,\ldots,y_n)-x/n]\right][x/n -p]p^{x}
(1-p)^{n-x}
\end{multline*}](img82.gif)
![]() is the UMVUE of p is one special case of
a general tactic.
is the UMVUE of p is one special case of
a general tactic.

![]() is held fixed at x. Notice
that the weights in this average do not depend on p. Notice that
this average is actually
is held fixed at x. Notice
that the weights in this average do not depend on p. Notice that
this average is actually

![]() the log likelihood
is
the log likelihood
is
