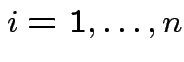 group
the observations into
group
the observations into
Problem: given observations ![]() for
for
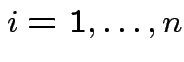 group
the observations into
group
the observations into ![]() populations.
populations.
Parallel to discriminant analysis but: no training data.
Here: just show some example analyses:
Cluster iris data: so ![]() presumably.
presumably.
Often: ![]() not known.
not known.
Many possible SPlus functions including: agnes, clara, pam, hclust
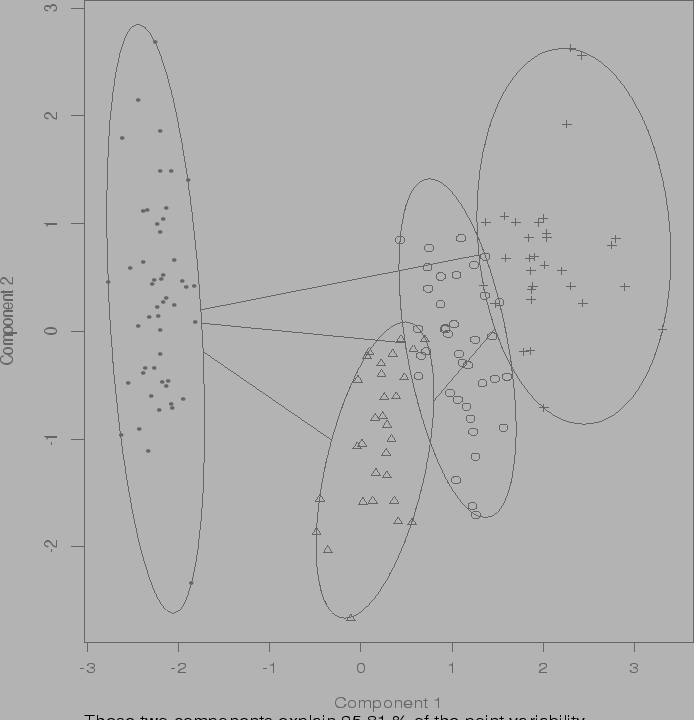
Example: Cluster the iris data.
Put all 150 observations into 150![]() 4 matrix. (Remove species
labels.)
4 matrix. (Remove species
labels.)
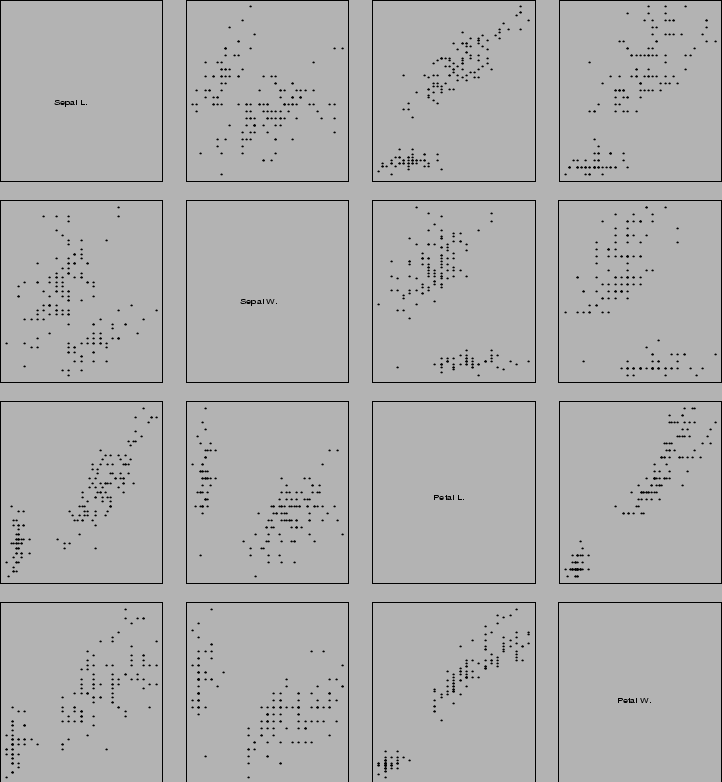
Cluster into 2, 3 ,4 groups using pam:
pamiris2 <- pam(x,2) pamiris3 <- pam(x,3) pamiris4 <- pam(x,4)Output for two clusters:
> pam(x,2)
Call: pam(x = x, k = 2)
Medoids:
Sepal L. Sepal W. Petal L. Petal W.
[1,] 5.0 3.4 1.5 0.2
[2,] 6.2 2.8 4.8 1.8
Clustering vector:
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[38] 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[75] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2
[112] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[149] 2 2
Notice that the algorithm correctly groups together the first 50 observations.
The other two species are then lumped together.
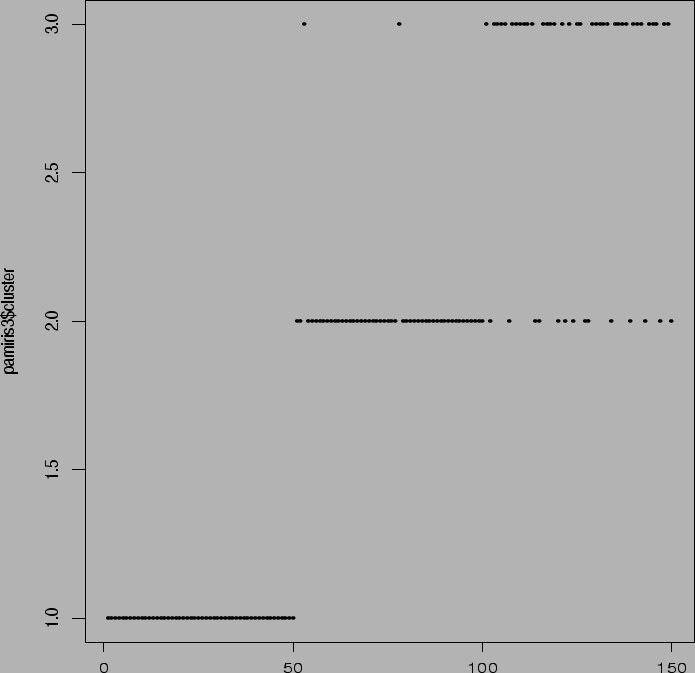
> pam(x,3)
Call:
pam(x = x, k = 3)
Medoids:
Sepal L. Sepal W. Petal L. Petal W.
[1,] 5.0 3.4 1.5 0.2
[2,] 6.0 2.9 4.5 1.5
[3,] 6.8 3.0 5.5 2.1
Clustering vector:
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[38] 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[75] 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 3 2 3 3 3 3 2 3 3 3 3
[112] 3 3 2 2 3 3 3 3 2 3 2 3 2 3 3 2 2 3
3 3 3 3 2 3 3 3 3 2 3 3 3 2 3 3 3 2 3
[149] 3 2
Notice difficulty with 2 versus 3. Total of two
from group 2 clustered into group 3; total of
14 from group 3 clustered into group 2.
Now a method which does not require specification of number of classes but doesn't estimate number of classes either. Hierarchical clustering.
> agnesiris <- agnes(x)
> cutree(agnesiris,k=2)
[1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[38] 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[112] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[149] 1 1
attr(, "height"):
[1] 0.8964852 0.2645751
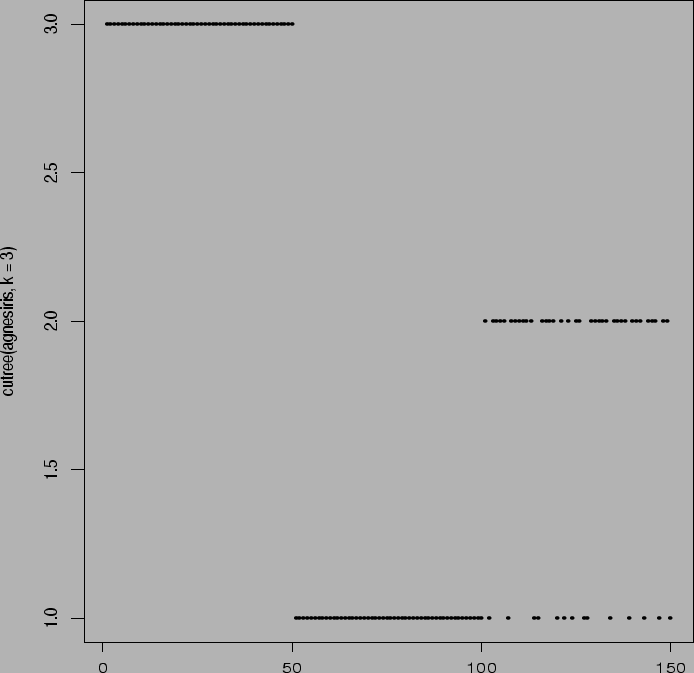
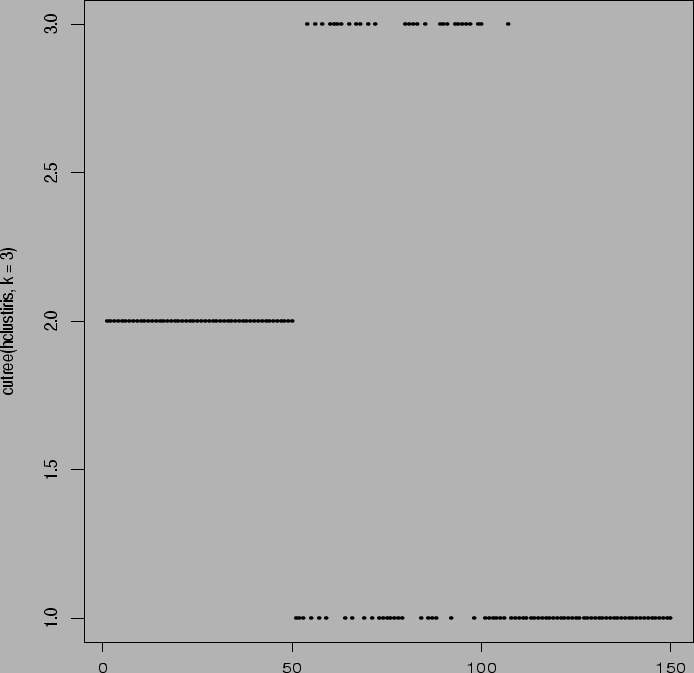
> plot(cutree(agnesiris,k=2))
> plot(cutree(agnesiris,k=3))
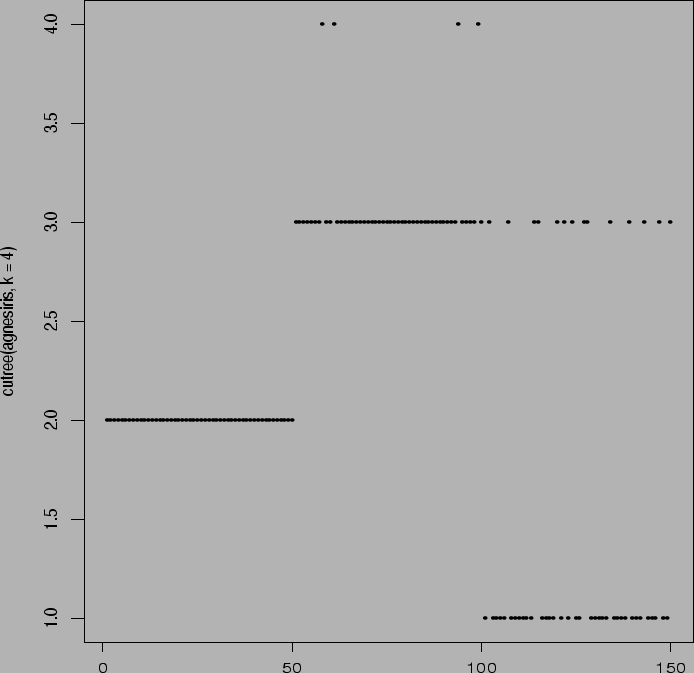
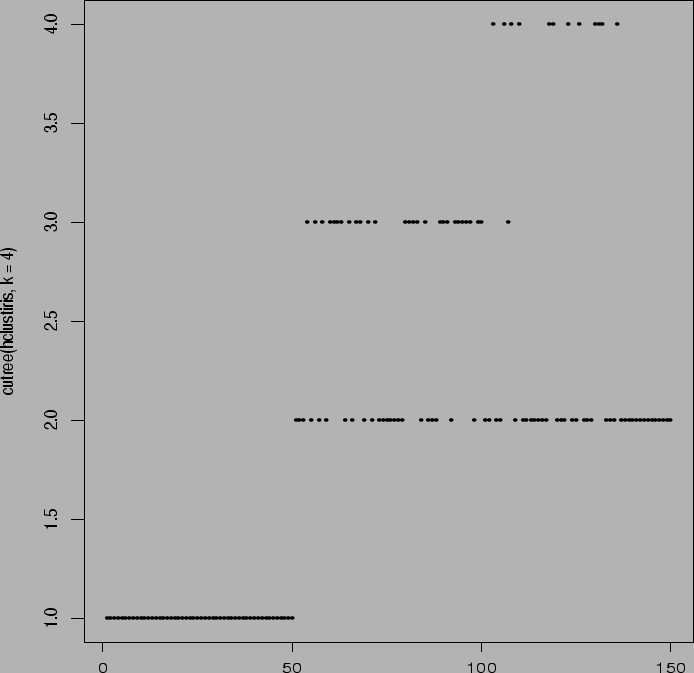
> plot(cutree(agnesiris,k=4))