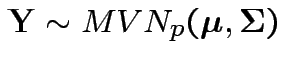 . Imagine that
. Imagine that
Suppose
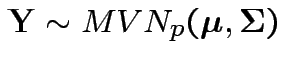 . Imagine that
. Imagine that ![]() is
a vector of scores on various tests.
is
a vector of scores on various tests.
Idea: study structure of
![]() or of
or of ![]() , look to see if
, look to see if ![]() is ``explained'' by
a small number of factors common to all variables together with
some variability in individual variability which is independent
between variables.
is ``explained'' by
a small number of factors common to all variables together with
some variability in individual variability which is independent
between variables.
This amounts to writing
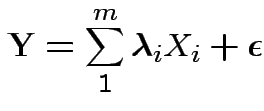
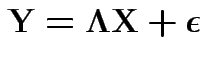
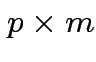 (hopefully with
(hopefully with
Then the variance covariance of ![]() has the form
has the form
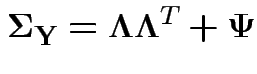
Specificities: (or specific variances or uniquenesses) -- the
![]() , the diagonal entries in
, the diagonal entries in
![]() .
.
Common factors: the variables
 .
.
Loading:
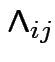 is the ``loading of the
is the ``loading of the ![]() th response
on the
th response
on the ![]() th common factor''.
th common factor''.
Communalities: The parts of the variances of the ![]() which
arise from the common factors, that is,
which
arise from the common factors, that is,
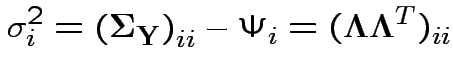
What can be estimated?
Given
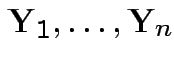 iid
iid
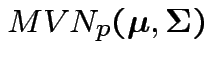 .
.
Assume
![]() has factor structure for
has factor structure for ![]() factors.
factors.
Log likelihood is
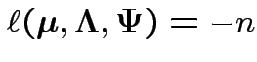 |
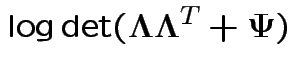 |
|
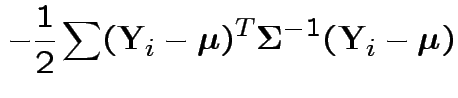 |
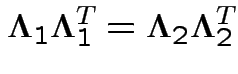
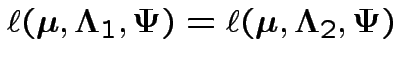
This means that ![]() is not identifiable.
is not identifiable.
If two parameter values each give the same density for the data then the data do not distinguish between the two parameter values.
In factor analysis we use subject matter understanding to try to
pick one particular
![]() from the collection
which maximize
from the collection
which maximize ![]() on the basis of external or a priori
criteria.
on the basis of external or a priori
criteria.
But: MLE of
![]() and
and
![]() possible.
possible.
| Case | Growth | Profit | New | Creat | Mech | Abst | Math |
| 1 | 93.0 | 96.0 | 97.8 | 9 | 12 | 9 | 20 |
| 2 | 88.8 | 91.8 | 96.8 | 7 | 10 | 10 | 15 |
| 3 | 95.0 | 100.3 | 99.0 | 8 | 12 | 9 | 26 |
data sales;
infile "T9-12.DAT";
input growth profit new
create mech abst math;
proc factor method=prin
rotate=none all;
run;
The (edited) output is
Initial Factor Method: Principal Components
Inverse Correlation Matrix
GROWTH PROFIT NEW CREATE MECH ABST MATH
GROWTH 35.14 -8.26 15.74 -13.90 -1.55 -13.86 -23.71
PROFIT -8.26 31.62 -2.70 1.41 -8.18 6.58 -19.50
NEW 15.74 -2.70 21.69 -13.24 -0.13 -10.46 -19.06
CREATE-13.90 1.41 -13.24 10.53 -0.12 7.64 14.25
MECH -1.55 -8.18 -0.13 -0.12 4.56 -0.88 7.22
ABST -13.86 6.58 -10.46 7.64 -0.88 8.68 7.99
MATH -23.71 -19.50 -19.06 14.25 7.22 7.99 43.09
Partial Correlations Controlling all other Variables
GROWTH PROFIT NEW CREATE MECH ABST MATH
GROWTH 1.000 0.248 -0.570 0.722 0.123 0.793 0.609
PROFIT 0.248 1.000 0.103 -0.077 0.681 -0.397 0.528
NEW -0.570 0.103 1.000 0.876 0.013 0.762 0.623
CREATE 0.722 -0.077 0.876 1.000 0.018 -0.798 -0.668
MECH 0.123 0.681 0.013 0.018 1.000 0.140 -0.515
ABST 0.793 -0.397 0.762 -0.798 0.140 1.000 -0.413
MATH 0.609 0.528 0.623 -0.668 -0.515 -0.413 1.000
Prior Communality Estimates: ONE
Eigenvalues of the Correlation Matrix:
Total = 7 Average = 1
1 2 3 4 5 6 7
Eigenvalue 5.0346 0.9335 0.4979 0.4212 0.0810 0.0203 0.0113
Difference 4.1011 0.4356 0.0767 0.3402 0.0607 0.0090
Proportion 0.7192 0.1334 0.0711 0.0602 0.0116 0.0029 0.0016
Cumulative 0.7192 0.8526 0.9237 0.9839 0.9955 0.9984 1.0000
1 factors will be retained by the MINEIGEN criterion.
Eigenvectors
GROWTH 0.43367
PROFIT 0.42021
NEW 0.42105
CREATE 0.29429
MECH 0.34909
ABST 0.28917
MATH 0.40740
Factor Pattern
FACTOR1
GROWTH 0.97307
PROFIT 0.94287
NEW 0.94475
CREATE 0.66032
MECH 0.78329
ABST 0.64883
MATH 0.91413
Variance explained by each factor
FACTOR1
5.034598
Communality Estimates: Total = 5.034598
GROWTH PROFIT NEW CREATE MECH ABST MATH
0.9468 0.8890 0.8925 0.4360 0.6135 0.4209 0.8356
Note: matrix of loadings called Factor Pattern.
Can estimate latent variables (Factor Scores).
Scoring Coefficients Estimated by Regression
Squared Multiple Correlations of
the Variables with each Factor
FACTOR1
1.000000
Standardized Scoring Coefficients
FACTOR1
GROWTH 0.19328
PROFIT 0.18728
NEW 0.18765
CREATE 0.13116
MECH 0.15558
ABST 0.12887
MATH 0.18157
Residual Correlations With Uniqueness on the Diagonal
GROWTH PROFIT NEW CREATE MECH ABST MATH
GROWTH 0.053 0.008 -0.035 -0.070 -0.054 0.043 0.037
PROFIT 0.008 0.110 -0.048 -0.081 0.007 -0.146 0.082
NEW -0.035 -0.048 0.107 0.076 -0.102 0.028 -0.011
CREATE -0.070 -0.081 0.076 0.563 0.073 -0.281 -0.190
MECH -0.054 0.007 -0.102 0.073 0.386 -0.122 -0.141
ABST 0.043 -0.146 0.028 -0.281 -0.122 0.579 -0.026
MATH 0.037 0.082 -0.011 -0.190 -0.141 -0.026 0.164
Root Mean Square Off-diagonal Residuals:
Over-all = 0.10322669
GROWTH PROFIT NEW CREATE MECH ABST MATH
0.0456 0.0787 0.0589 0.1519 0.0947 0.1408 0.1045
Partial Correlations Controlling Factors
GROWTH PROFIT NEW CREATE MECH ABST MATH
GROWTH 1.000 0.111 -0.467 -0.407 -0.377 0.245 0.404
PROFIT 0.111 1.000 -0.441 -0.324 0.035 -0.577 0.609
NEW -0.467 -0.441 1.000 0.310 -0.503 0.112 -0.083
CREATE -0.407 -0.324 0.310 1.000 0.157 -0.492 -0.627
MECH -0.377 0.035 -0.503 0.157 1.000 -0.258 -0.561
ABST 0.245 -0.577 0.112 -0.492 -0.258 1.000 -0.086
MATH 0.404 0.609 -0.083 -0.627 -0.561 -0.086 1.000
Root Mean Square Off-diagonal Partials:
Over-all = 0.38975152
GROWTH PROFIT NEW CREATE MECH ABST MATH
0.3566 0.4122 0.3612 0.4140 0.3660 0.3472 0.4580
The procedure selects only one factor on which all the variables are fairly
highly loaded. The factor is the first principal component of the
correlation matrix.
Now insist on two factors, use varimax rotation and plot factor loadings before and after rotation.
proc factor m=prin nfactor=2 rotate=v
preplot plot all;
The output
Factor Pattern
FACTOR1 FACTOR2
GROWTH 0.97307 -0.10798
PROFIT 0.94287 0.02830
NEW 0.94475 0.00889
CREATE 0.66032 0.64581
MECH 0.78329 0.28497
ABST 0.64883 -0.62066
MATH 0.91413 -0.19359
Variance explained by each factor
FACTOR1 FACTOR2
5.034598 0.933516
Plot of Factor Pattern for FACTOR1 and FACTOR2
FACTOR1
1
A B
G .9
.8 E
.7
F D
.6
.5
.4
.3
.2
F
.1 A
C
-.7-.6-.5-.4-.3-.2-.1 0 .1 .2 .3 .4 .5 .6 .7 .8 T
O
-.1 R
2
-.2
GROWTH=A PROFIT=B NEW=B CREATE=D MECH=E ABST=F MATH=G
Rotation Method: Varimax
Orthogonal Transformation Matrix
1 2
1 0.73145 0.68189
2 -0.68189 0.73145
Rotated Factor Pattern
FACTOR1 FACTOR2
GROWTH 0.78538 0.58455
PROFIT 0.67037 0.66364
NEW 0.68498 0.65072
CREATE 0.04261 0.92265
MECH 0.37862 0.74256
ABST 0.89781 -0.01155
MATH 0.80065 0.48174
Variance explained by each factor
FACTOR1 FACTOR2
3.127683 2.840431
Plot of Factor Pattern for FACTOR1 and FACTOR2
FACTOR1
1
F9
.8 G A
.7 C
B
.6
.5
.4 E
.3
.2
F
.1 A
D C
-.7-.6-.5-.4-.3-.2-.1 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1.0T
O
-.1 R
2
GROWTH=A PROFIT=B NEW=C CREATE=D MECH=E ABST=F MATH=G
With principal components factor analysis fitting a second factor does
not change the first factor (before rotation). Creativity and
abstract reasoning are loaded on the second factor with opposite signs
which would appear to represent a difference between people on a dimension of
creativity as opposed to abstract reasoning.
After rotation everything except creativity is loaded on factor 1, though Mechanical reasoning has a rather smaller loading. Abstraction is not loaded on factor 2.
Now I tried iterated principal factor analysis with varimax rotation. The option heywood permits iteration to continue if the estimated uniqueness of a variable drops below 0.
proc factor m=prinit nfactor=2 rotate=v
preplot plot all heywood;
run;
Initial Factor Method:
Iterated Principal Factor Analysis
Prior Communality Estimates: ONE
2 factors will be retained by the NFACTOR criterion.
IterChange Communalities
1 0.3052 0.958 0.889 0.892 0.853 0.694 0.806 0.873
2 0.1223 0.968 0.874 0.879 0.805 0.600 0.683 0.850
3 0.0903 0.980 0.874 0.880 0.797 0.574 0.593 0.855
4 0.0638 0.988 0.876 0.881 0.807 0.568 0.529 0.866
5 0.0401 0.993 0.877 0.882 0.824 0.564 0.489 0.878
6 0.0229 0.995 0.879 0.882 0.844 0.562 0.466 0.886
7 0.0191 0.996 0.880 0.882 0.863 0.560 0.453 0.892
8 0.0183 0.996 0.880 0.882 0.881 0.558 0.447 0.895
9 0.0174 0.996 0.880 0.881 0.899 0.556 0.443 0.897
10 0.0165 0.996 0.881 0.881 0.915 0.554 0.440 0.899
11 0.0156 0.996 0.881 0.880 0.931 0.552 0.438 0.899
12 0.0148 0.996 0.881 0.880 0.946 0.551 0.437 0.899
13 0.0141 0.996 0.881 0.879 0.960 0.549 0.436 0.899
14 0.0135 0.996 0.881 0.879 0.973 0.548 0.435 0.899
15 0.0129 0.995 0.881 0.879 0.986 0.547 0.434 0.899
16 0.0124 0.995 0.882 0.878 0.999 0.546 0.433 0.899
17 0.0010 0.995 0.882 0.878 1.000 0.545 0.432 0.899
18 0.0002 0.996 0.882 0.878 1.000 0.544 0.432 0.899
Convergence criterion satisfied.
Eigenvalues of the Reduced Correlation Matrix:
Total = 5.63350769 Average = 0.80478681
1 2 3
Eigenvalue 4.8786 0.7663 0.2047
Difference 4.1123 0.5616 0.1209
Proportion 0.8660 0.1360 0.0363
Cumulative 0.8660 1.0020 1.0384
Eigenvectors
1 2
GROWTH 0.44687 -0.16852
PROFIT 0.42379 -0.08882
NEW 0.42404 0.03803
CREATE 0.30550 0.85228
MECH 0.32820 0.15943
ABST 0.26439 -0.34496
MATH 0.41224 -0.30243
Factor Pattern
FACTOR1 FACTOR2
GROWTH 0.98704 -0.14753
PROFIT 0.93605 -0.07775
NEW 0.93660 0.03329
CREATE 0.67478 0.74609
MECH 0.72492 0.13956
ABST 0.58396 -0.30198
MATH 0.91054 -0.26475
Plot of Factor Pattern for FACTOR1 and FACTOR2
FACTOR1
A 1
B C
G .9
.8
.7 E
D
F .6
.5
.4
.3
.2
F
.1 A
C
-.7-.6-.5-.4-.3-.2-.1 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1.0T
O
-.1 R
2
GROWTH=A PROFIT=B NEW=C CREATE=D MECH=E ABST=F MATH=G
Rotation Method: Varimax
Orthogonal Transformation Matrix
1 2
1 0.84716 0.53133
2 -0.53133 0.84716
Rotated Factor Pattern
FACTOR1 FACTOR2
GROWTH 0.91457 0.39946
PROFIT 0.83430 0.43149
NEW 0.77577 0.52585
CREATE 0.17523 0.99059
MECH 0.53997 0.50340
ABST 0.65516 0.05445
MATH 0.91205 0.25951
Variance explained by each factor
FACTOR1 FACTOR2
3.717650 1.927275
Plot of Factor Pattern for FACTOR1 and FACTOR2
FACTOR1
1
.9 G A
B
.8 C
.7
F
.6
E
.5
.4
.3
.2 D
F
.1 A
C
-.7-.6-.5-.4-.3-.2-.1 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1.0T
O
-.1 R
2
GROWTH=A PROFIT=B NEW=C CREATE=D MECH=E ABST=F MATH=G
The rotated factor loadings seem rather similar here. There seems to be
a distinct latent variable which fully explains creativity and is at
play in determining other variables a bit. There also seems to be a
variable on which every variable except creativity is highly loaded.
I am not really sure how to interpret this variable.
Now I tried maximum likelihood.
proc factor m=ml nfactor=2 rotate=v
preplot plot all heywood;
run;
The output is
Significance tests based on 50 observations:
Test of H0: No common factors.
vs HA: At least one common factor.
Chi-square = 499.661 df = 21 Prob>chi**2 = 0.0001
Test of H0: 2 Factors are sufficient.
vs HA: More factors are needed.
Chi-square = 117.092 df = 8 Prob>chi**2 = 0.0001
Notice ML conclusion: not enough factors.
FACTOR1 FACTOR2
GROWTH 0.57204 0.77709
PROFIT 0.54151 0.79768
NEW 0.70036 0.62138
CREATE 1.00000 -0.00000
MECH 0.59074 0.42024
ABST 0.14691 0.60579
MATH 0.41264 0.89462
Plot of Factor Pattern for FACTOR1 and FACTOR2
FACTOR1
D
.9
.8
.7 C
.6 E
A
.5
.4 G
.3
.2
F
.1
-.7-.6-.5-.4-.3-.2-.1 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1.0
GROWTH=A PROFIT=A NEW=C CREATE=D MECH=E ABST=F MATH=G
Rotation Method: Varimax Rotated Factor Pattern
FACTOR1 FACTOR2
GROWTH 0.85249 0.45205
PROFIT 0.86839 0.41884
NEW 0.71725 0.60180
CREATE 0.14646 0.98922
MECH 0.50223 0.52282
ABST 0.62078 0.05660
MATH 0.94541 0.27716
FACTOR1
G
.9
BA
.8
.7 C
.6F
.5 E
.4
.3
.2
D
.1
-.7-.6-.5-.4-.3-.2-.1 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1.0
GROWTH=A PROFIT=B NEW=C CREATE=D MECH=E ABST=F MATH=G
Pattern same as for other methods.
Notice however, that this
procedure factors ![]() not
not ![]() .
.
This explains the totally different eigenvalues and so on.
Finally I ran proc glm regressing the sales figures on the psychological test scores.
proc glm ; model growth profit new = create mech abst math; manova h=_all_ /printh printe; run;The output is:
Dependent Variable: GROWTH Source DF TypeIIISS Mean Sqe F Pr > F CREATE 1 61.43176 61.4317 23.53 0.0001 MECH 1 25.57000 25.5700 9.79 0.0031 ABST 1 92.58581 92.5858 35.46 0.0001 MATH 1 548.00956 548.0095 209.87 0.0001 Dependent Variable: PROFIT Source DF Type IIISS Mean Sq F Pr > F CREATE 1 6.79727 6.79727 1.80 0.1860 MECH 1 213.27427 213.27427 56.58 0.0001 ABST 1 48.81780 48.81780 12.95 0.0008 MATH 1 1764.23024 1764.23024 468.05 0.0001 Dependent Variable: NEW Source DF TypeIIISS Mean Sq F Pr > F CREATE 1 153.40826 153.408 92.69 0.0001 MECH 1 1.84667 1.846 1.12 0.2965 ABST 1 63.38081 63.380 38.30 0.0001 MATH 1 150.95169 150.951 91.21 0.0001All the variables are very significant predictors of the sales indices.
Type 3 Sums of Squares, which adjust for all other variables in the model are the relevant ones.
They show that from a multivariate point of view no variables can be deleted.
But:in univariate regression for PROFIT can probability drop Creativity while for predicting NEW sales Mechanical reasoning appears unimportant.
All 4 must be retained for prediction of sales growth.
So far as I can see this data set is relatively well understood from this
regression output, though the correlation structure is of some interest
too.