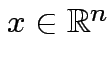 are column vectors
are column vectors
![$\displaystyle x=\left[\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right]
$](img2.gif)
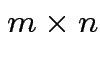 matrix
matrix 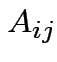 .
.
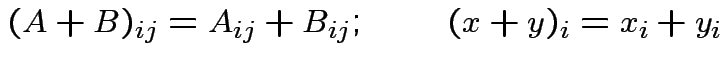
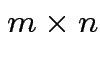 and
and 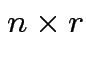 then
then 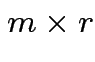 matrix
matrix
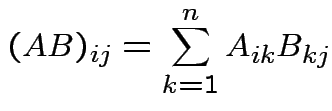
Notation:
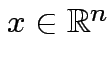 are column vectors
are column vectors
![$\displaystyle x=\left[\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right]
$](img2.gif)
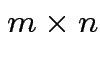 matrix
matrix 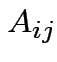 .
.
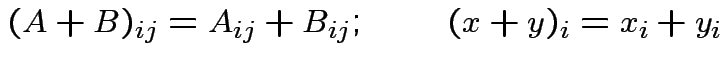
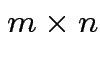 and
and 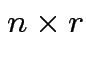 then
then 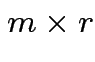 matrix
matrix
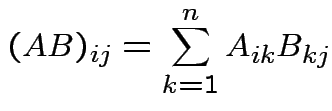
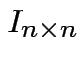 which is an
which is an
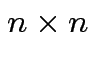 matrix with
matrix with
 for all
for all 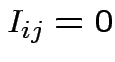 for any pair
for any pair
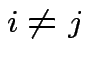 is called the
is called the 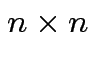 identity matrix.
identity matrix.
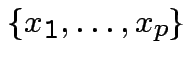 is the
set of all vectors
is the
set of all vectors  . It is a vector space.
The column space of a matrix,
. It is a vector space.
The column space of a matrix,
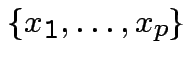 is linearly independent
if
is linearly independent
if
 implies
implies 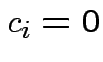 for all
for all
Defn: The transpose, ![]() , of an
, of an 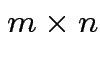 matrix
matrix ![]() is
the
is
the
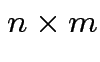 matrix whose entries are given by
matrix whose entries are given by
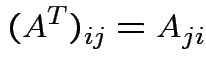
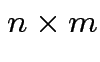 . We have
. We have
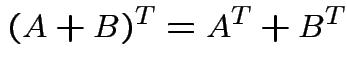
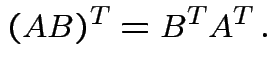
Defn: rank of matrix ![]() ,
rank
,
rank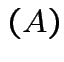 :
# of linearly independent
columns of
:
# of linearly independent
columns of ![]() .
We have
.
We have
rank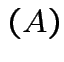 |
||
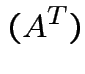 |
If ![]() is
is
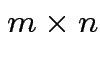 then
rank
then
rank .
.
For now: all matrices square
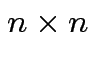 .
.
If there is a matrix ![]() such that
such that
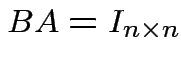 then
we call
then
we call ![]() the inverse of
the inverse of ![]() . If
. If ![]() exists it is unique and
exists it is unique and
![]() and we write
and we write ![]() . The matrix
. The matrix ![]() has an inverse if and only
if
rank
has an inverse if and only
if
rank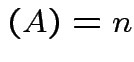 .
.
Inverses have the following properties:
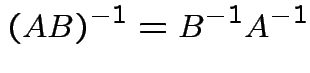

Again ![]() is
is  . The determinant if a function on the set
of
. The determinant if a function on the set
of
 matrices such that:
matrices such that:
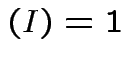 .
.
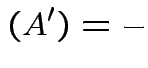 det
det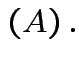
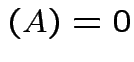 .)
.)
 is a linear function of each column of
is a linear function of each column of 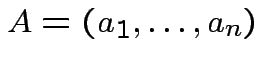 with
with det |
 |
|
det |
||
 |
Here are some properties of the determinant:
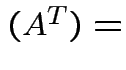 det
det .
.
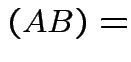 det
det det
det .
.
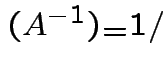 det
det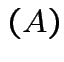 .
.
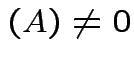 if and only if
rank
if and only if
rank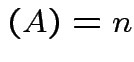 .
.
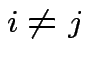 implies
implies  .
.
Defn: Two vectors ![]() and
and ![]() are orthogonal if
are orthogonal if
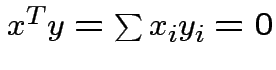 .
.
Defn: The inner product or dot product of ![]() and
and ![]() is
is

Defn: ![]() and
and ![]() are orthogonal if
are orthogonal if 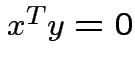 .
.
Defn: The norm (or length) of ![]() is
is
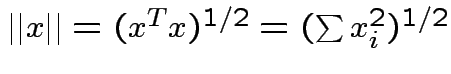
![]() is orthogonal if each column of
is orthogonal if each column of ![]() has length 1 and
is orthogonal to each other column of
has length 1 and
is orthogonal to each other column of ![]() .
.
Suppose ![]() is an
is an
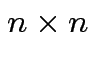 matrix. The function
matrix. The function
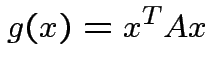
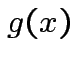 |
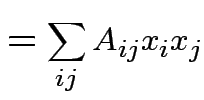 |
|
 |
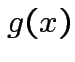 depends only on the total
depends only on the total
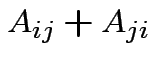 . In
fact
. In
fact

If ![]() is
is
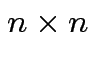 and
and
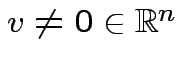 and
and
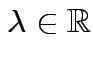 such that
such that
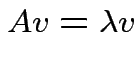
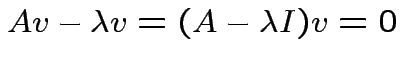 matrix
matrix
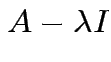 is singular.
is singular.
Therefore
det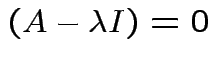 .
.
Conversely: if
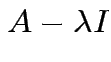 singular
then there is
singular
then there is  such that
such that
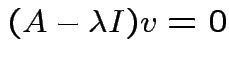 .
.
Fact:
det is polynomial in
is polynomial in ![]() of degree
of degree
![]() .
.
Each root is an eigenvalue.
General ![]() the roots could be
multiple roots or complex valued.
the roots could be
multiple roots or complex valued.
Matrix ![]() is diagonalized by a non-singular matrix
is diagonalized by a non-singular matrix
![]() if
if
![]() is diagonal.
is diagonal.
If so then ![]() so each column of
so each column of ![]() is eigenvector of
is eigenvector of ![]() with
the
with
the ![]() th column having eigenvalue
th column having eigenvalue 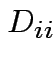 .
.
Thus to be diagonalizable
![]() must have
must have ![]() linearly independent eigenvectors.
linearly independent eigenvectors.
If ![]() is symmetric then
is symmetric then
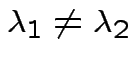 are two eigenvalues of
are two eigenvalues of 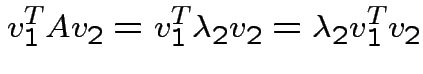
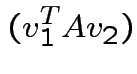 |
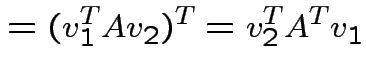 |
|
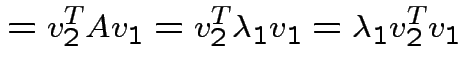 |
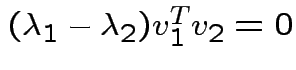 and
and
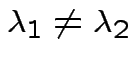 we see
we see
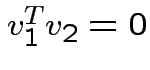 . Eigenvectors corresponding
to distinct eigenvalues are orthogonal.
. Eigenvectors corresponding
to distinct eigenvalues are orthogonal.
Defn: A symmetric matrix ![]() is non-negative definite if
is non-negative definite if
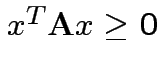 for all
for all ![]() . It is positive definite if in addition
. It is positive definite if in addition
![]() implies
implies
![]() .
.
![]() is non-negative definite iff all its eigenvalues are
non-negative.
is non-negative definite iff all its eigenvalues are
non-negative.
![]() is positive definite iff all eigenvalues positive.
is positive definite iff all eigenvalues positive.
A non-negative definite matrix has a symmetric non-negative definite square root. If
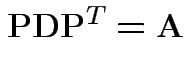
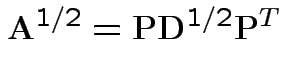
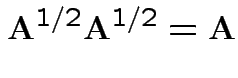

 .
.
Suppose ![]() vector subspace of
vector subspace of
![]() ,
,
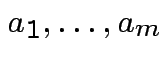 basis for
basis for ![]() . Given any
. Given any
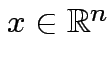 there
is a unique
there
is a unique 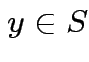 which is closest to
which is closest to ![]() ;
; ![]() minimizes
minimizes

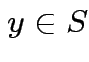 . Any
. Any 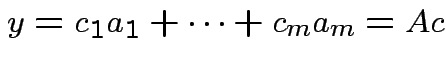
 , columns
, columns
 ;
;
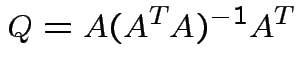
 |
||
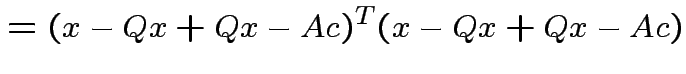 |
||
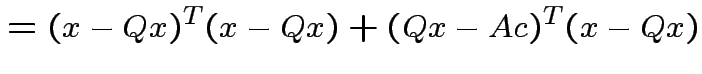 |
||
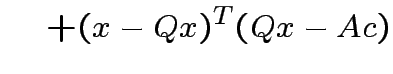 |
||
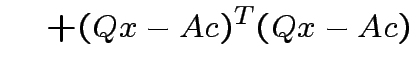 |
Note that
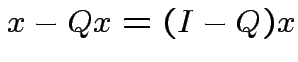 and that
and that

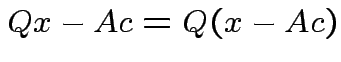
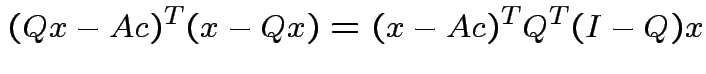
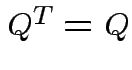 we see that
we see that
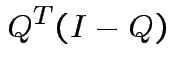 |
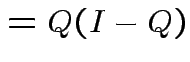 |
|
 |
||
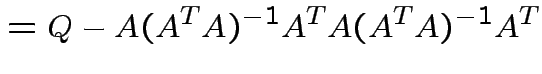 |
||
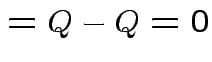 |
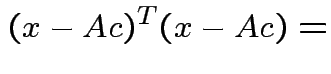 |
 |
|
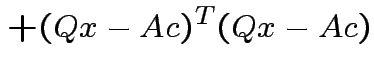 |
Choose ![]() to minimize:
minimize second term.
to minimize:
minimize second term.
Achieved by making
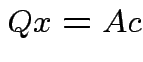 .
.
Since
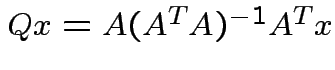 can
take
can
take
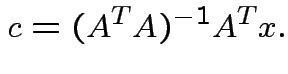
Summary:
closest point ![]() in
in ![]() is
is
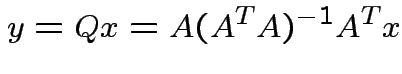
Notice that the matrix ![]() is idempotent:
is idempotent:
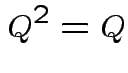
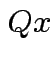 the orthogonal projection of
the orthogonal projection of 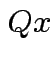 is perpendicular to the residual
is perpendicular to the residual
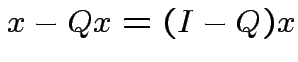 .
.
Suppose 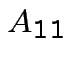
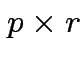 matrix,
matrix, 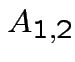
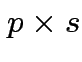 ,
, 
 and
and 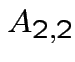
 . Make
. Make
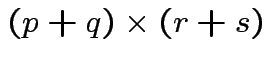 matrix
by putting
matrix
by putting 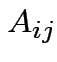 in 2 by 2 matrix:
in 2 by 2 matrix:
![$\displaystyle A = \left[ \begin{array}{cc}
A_{11} & A_{12}
\\
A_{21} & A_{22}
\end{array}\right]
$](img166.gif)
![$\displaystyle A_{11} = \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]
$](img167.gif)
![$\displaystyle A_{12} = \left[ \begin{array}{c} 2 \\ 3 \end{array}\right]
$](img168.gif)
![$\displaystyle A_{21} = \left[ \begin{array}{cc} 4 & 5\end{array}\right]
$](img169.gif)
![$\displaystyle A_{22} = \left[ 6 \right]
$](img170.gif)
![$\displaystyle A = \left[ \begin{array}{cc\vert c}
1 & 0 & 2
\\
0 & 1 & 3
\\
\hline
4 & 5 & 6
\end{array}\right]
$](img171.gif)
We can work with partitioned matrices just like ordinary matrices always making sure that in products we never change the order of multiplication of things.
![$\displaystyle \left[ \begin{array}{cc} A_{11} & A_{12} \\ \\ A_{21} & A_{22} \end{array} \right]$](img172.gif) |
![$\displaystyle + \left[ \begin{array}{cc} B_{11} & B_{12} \\ \\ B_{21} & B_{22} \end{array} \right]$](img173.gif) |
|
![$\displaystyle \left[ \begin{array}{cc} A_{11}+B_{11} & A_{12}+B_{12} \\ \\ A_{21}+B_{21} & A_{22}+B_{22} \end{array} \right]$](img174.gif) |
![\begin{multline*}
\left[ \begin{array}{cc}
A_{11} & A_{12}
\\
\\
A_{21} & A_{2...
...{11}+A_{22}B_{21} &A_{21}B_{12}+ A_{22}B_{22}
\end{array}\right]
\end{multline*}](img175.gif)
Note partitioning of ![]() and
and ![]() must match.
must match.
Addition: dimensions of 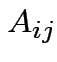 and
and 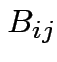 must be the same.
must be the same.
Multiplication formula  must
have as many columns as
must
have as many columns as  has rows, etc.
has rows, etc.
In general:
need
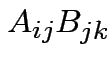 to make sense for each
to make sense for each 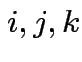 .
.
Works with more than a 2 by 2 partitioning.
Defn: block diagonal matrix: partitioned matrix ![]() for which
for which  if
if 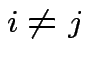 . If
. If
![$\displaystyle A = \left[ \begin{array}{cc}
A_{11} & 0
\\
0 & A_{22}
\end{array}\right]
$](img181.gif)
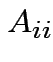 is invertible and
then
is invertible and
then
![$\displaystyle A^{-1} = \left[ \begin{array}{cc}
A_{11}^{-1} & 0
\\
0 & A_{22}^{-1}
\end{array}\right]
$](img183.gif)
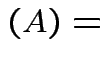 det
det det
det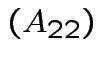 .
Similar formulas work for larger matrices.
.
Similar formulas work for larger matrices.
Partitioned inverses. Suppose ![]() ,
, ![]() are symmetric positive
definite. Look for inverse of
are symmetric positive
definite. Look for inverse of
![$\displaystyle \left[\begin{array}{cc} {\bf A}& {\bf B}\\ {\bf B}^T & {\bf C}\end{array}\right]
$](img188.gif)
![$\displaystyle \left[\begin{array}{cc} {\bf E}& {\bf F}\\ {\bf F}^T & {\bf G}\end{array}\right]
$](img189.gif)
 |
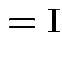 |
|
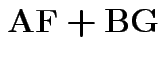 |
 |
|
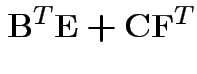 |
 |
|
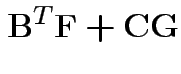 |
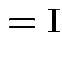 |
Solve to get
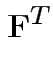 |
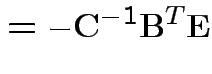 |
|
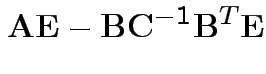 |
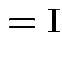 |
|
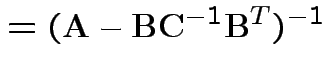 |
||
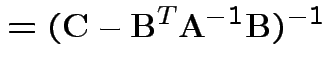 |