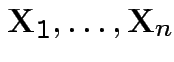 iid
iid
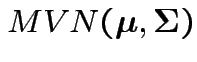 test
test
Given data
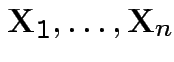 iid
iid
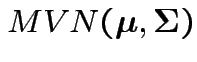 test
test
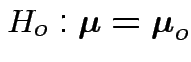
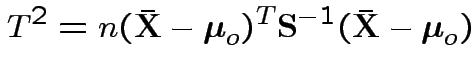
Example: no realistic ones. This hypothesis is not intrinsically useful. However: other tests can sometimes be reduced to it.
Example: Ten water samples split in half. One half of each
to each of two labs. Measure biological oxygen demand (BOD) and
suspended solids (SS). For sample ![]() let
let 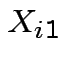 be BOD for lab A,
be BOD for lab A,
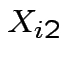 be SS for lab A,
be SS for lab A, 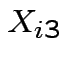 be BOD for lab B and
be BOD for lab B and 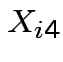 be
SS for lab B. Question: are labs measuring the same thing? Is there
bias in one or the other?
be
SS for lab B. Question: are labs measuring the same thing? Is there
bias in one or the other?
Notation ![]() is vector of 4 measurements on sample
is vector of 4 measurements on sample ![]() .
.
Data:
| Lab A | Lab B | |||
| Sample | BOD | SS | BOD | SS |
| 1 | 6 | 27 | 25 | 15 |
| 2 | 6 | 23 | 28 | 13 |
| 3 | 18 | 64 | 36 | 22 |
| 4 | 8 | 44 | 35 | 29 |
| 5 | 11 | 30 | 15 | 31 |
| 6 | 34 | 75 | 44 | 64 |
| 7 | 28 | 26 | 42 | 30 |
| 8 | 71 | 124 | 54 | 64 |
| 9 | 43 | 54 | 34 | 56 |
| 10 | 33 | 30 | 29 | 20 |
| 11 | 20 | 14 | 39 | 21 |
Model:
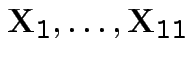 are iid
are iid
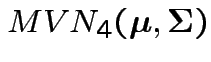 .
.
Multivariate problem because: not able to assume independence between any two measurements on same sample.
Potential sub-model: each measurement is
true mmnt + lab bias + mmnt error.
Model for measurement error vector
![]() is multivariate normal mean 0 and diagonal covariance
matrix
is multivariate normal mean 0 and diagonal covariance
matrix
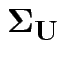 .
.
Lab bias is unknown vector
![]() .
.
True measurement should be same for both labs so has form
![$\displaystyle [Y_{i1},Y_{i2},Y_{i1},Y_{i2}]
$](img18.gif)
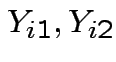 are iid bivariate normal with unknown
means
are iid bivariate normal with unknown
means
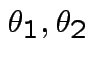 and unknown
and unknown
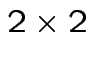 variance
covariance
variance
covariance
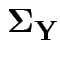 .
.
This would give structured model
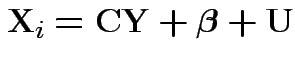
![$\displaystyle {\bf C}= \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 &
1\end{array}\right]
$](img24.gif)
This model has variance covariance matrix
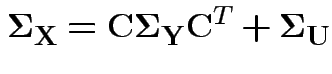
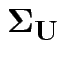 and 3 for the entries in
and 3 for the entries in
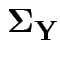 .
.
We skip this model and let
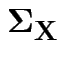 be unrestricted.
be unrestricted.
Question of interest:
 and
and 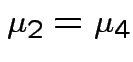
Reduction: partition ![]() as
as
![$\displaystyle \left[\begin{array}{c} {\bf U}_i \\ {\bf V}_i \end{array}\right]
$](img29.gif)
Define
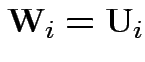 . Then our model makes
. Then our model makes 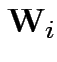 iid
iid
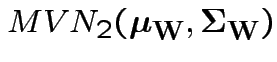 .
Our hypothesis is
.
Our hypothesis is
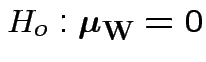
Carrying out our test in SPlus:
Working on CSS unix workstation:
Start SPlus then read in, print out data:
[61]ehlehl% mkdir .Data
[62]ehlehl% Splus
S-PLUS : Copyright (c) 1988, 1996 MathSoft, Inc.
S : Copyright AT&T.
Version 3.4 Release 1 for Sun SPARC, SunOS 5.3 : 1996
Working data will be in .Data
> # Read in and print out data
> eff <- read.table("effluent.dat",header=T)
> eff
BODLabA SSLabA BODLabB SSLabB
1 6 27 25 15
2 6 23 28 13
3 18 64 36 22
4 8 44 35 29
5 11 30 15 31
6 34 75 44 64
7 28 26 42 30
8 71 124 54 64
9 43 54 34 56
10 33 30 29 20
11 20 14 39 21
Do some graphical preliminary analysis.
Look for non-normality, non-linearity, outliers.
Make plots on screen or saved in file.
> # Make pairwise scatterplots on screen using
> # motif graphics device and then in a postscript
> # file.
> motif()
> pairs(eff)
> postscript("pairs.ps",horizontal=F,
+ height=6,width=6)
> pairs(eff)
> dev.off()
Generated postscript file "pairs.ps".
motif
2
> cor(eff)
BODLabA SSLabA BODLabB SSLabB
BODLabA 0.9999999 0.7807413 0.7228161 0.7886035
SSLabA 0.7807413 1.0000000 0.6771183 0.7896656
BODLabB 0.7228161 0.6771183 1.0000001 0.6038079
SSLabB 0.7886035 0.7896656 0.6038079 1.0000001
Notice high correlations.
Mostly caused by variation in true levels from sample to sample.
Get partial correlations.
Adjust for overall BOD and SS content of sample.
> aug <- cbind(eff,(eff[,1]+eff[,3])/2, + (eff[,2]+eff[,4])/2) > aug BODLabA SSLabA BODLabB SSLabB X2 X3 1 6 27 25 15 15.5 21.0 2 6 23 28 13 17.0 18.0 3 18 64 36 22 27.0 43.0 4 8 44 35 29 21.5 36.5 5 11 30 15 31 13.0 30.5 6 34 75 44 64 39.0 69.5 7 28 26 42 30 35.0 28.0 8 71 124 54 64 62.5 94.0 9 43 54 34 56 38.5 55.0 10 33 30 29 20 31.0 25.0 11 20 14 39 21 29.5 17.5 > bigS <- var(aug)
Now compute partial correlations for first four variables given means of BOD and SS:
> S11 <- bigS[1:4,1:4]
> S12 <- bigS[1:4,5:6]
> S21 <- bigS[5:6,1:4]
> S22 <- bigS[5:6,5:6]
> S11dot2 <- S11 - S12 %*% solve(S22,S21)
> S11dot2
BODLabA SSLabA BODLabB SSLabB
BODLabA 24.804665 -7.418491 -24.804665 7.418491
SSLabA -7.418491 59.142084 7.418491 -59.142084
BODLabB -24.804665 7.418491 24.804665 -7.418491
SSLabB 7.418491 -59.142084 -7.418491 59.142084
> S11dot2SD <- diag(sqrt(diag(S11dot2)))
> S11dot2SD
[,1] [,2] [,3] [,4]
[1,] 4.980428 0.000000 0.000000 0.000000
[2,] 0.000000 7.690389 0.000000 0.000000
[3,] 0.000000 0.000000 4.980428 0.000000
[4,] 0.000000 0.000000 0.000000 7.690389
> R11dot2 <- solve(S11dot2SD)%*%
+ S11dot2%*%solve(S11dot2SD)
> R11dot2
[,1] [,2] [,3] [,4]
[1,] 1.000000 -0.193687 -1.000000 0.193687
[2,] -0.193687 1.000000 0.193687 -1.000000
[3,] -1.000000 0.193687 1.000000 -0.193687
[4,] 0.193687 -1.000000 -0.193687 1.000000
Notice little residual correlation.
Carry out Hotelling's 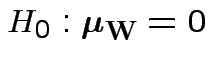 .
.
> w <- eff[,1:2]-eff[3:4]
> dimnames(w)<-list(NULL,c("BODdiff","SSdiff"))
> w
BODdiff SSdiff
[1,] -19 12
[2,] -22 10
etc
[8,] 17 60
etc
> Sw <- var(w)
> cor(w)
BODdiff SSdiff
BODdiff 1.0000001 0.3057682
SSdiff 0.3057682 1.0000000
> mw <- apply(w,2,mean)
> mw
BODdiff SSdiff
-9.363636 13.27273
> Tsq <- 11*mw%*%solve(Sw,mw)
> Tsq
[,1]
[1,] 13.63931
> FfromTsq <- (11-2)*Tsq/(2*(11-1))
> FfromTsq
[,1]
[1,] 6.13769
> 1-pf(FfromTsq,2,9)
[1] 0.02082779
Conclusion: Pretty clear evidence of difference in mean level between
labs.
Which measurement causes the difference?
> TBOD <- sqrt(11)*mw[1]/sqrt(Sw[1,1])
> TBOD
BODdiff
-2.200071
> 2*pt(TBOD,1)
BODdiff
0.2715917
> 2*pt(TBOD,10)
BODdiff
0.05243474
> TSS <- sqrt(11)*mw[2]/sqrt(Sw[2,2])
> TSS
SSdiff
2.15153
> 2*pt(-TSS,10)
SSdiff
0.05691733
> postscript("differences.ps",
+ horizontal=F,height=6,width=6)
> plot(w)
> abline(h=0)
> abline(v=0)
> dev.off()
Conclusion? Neither? Not a problem - summarizes evidence!
Problem: several tests at level 0.05 on same data. Simultaneous or Multiple comparisons.
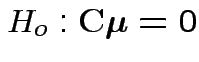 by computing
by computing
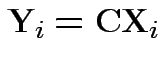 and then testing
and then testing
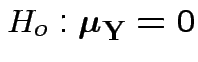 using Hotelling's
using Hotelling's
Confidence interval for
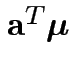 :
:
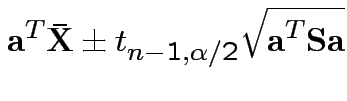
Give coverage intervals for 6 parameters of interest: 4 entries in
![]() and
and
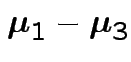 and
and
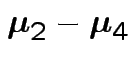
|
|
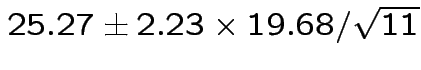 |
|
|
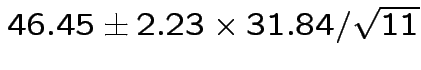 |
|
|
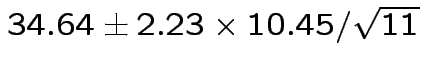 |
|
|
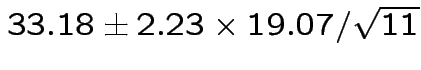 |
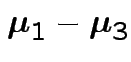 |
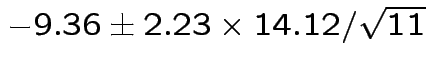 |
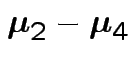 |
 |
Problem: each confidence interval has 5% error rate. Pick out last interval (on basis of looking most interesting) and ask about error rate?
Solution: adjust 2.23, ![]() multiplier to get
multiplier to get
 all intervals cover truth
all intervals cover truth
Based on inequality:
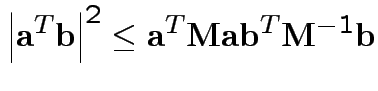
Proof by Cauchy Schwarz:
inner product of vectors
![]() and
and
![]() .
.
Put
 and
and
![]() to get
to get
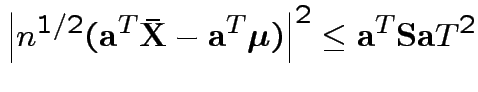
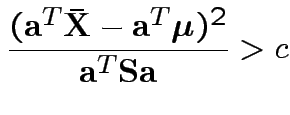
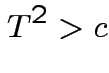
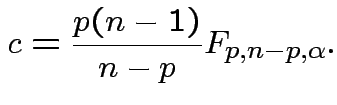
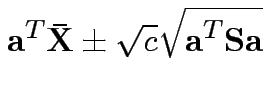
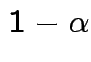 .
.
In fact the probability of this happening is exactly equal to 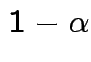 because for
each data set the supremum of
because for
each data set the supremum of
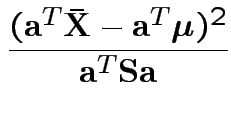
Our case
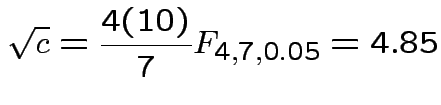
Coverage probability of single interval using
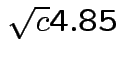 ?
From
?
From ![]() distribution:
distribution:

Probability all 6 intervals would cover using
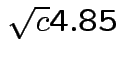 ?
?
Use Bonferroni inequality:
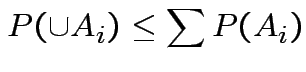
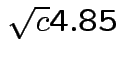

Usually just use
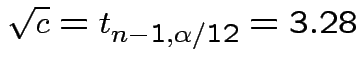
General Bonferroni strategy. If we want intervals for
 get interval for
get interval for ![]() at
level
at
level
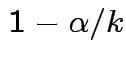 . Simultaneous coverage probability is
at least
. Simultaneous coverage probability is
at least 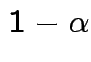 . Notice that Bonferroni narrower in
our example unless
. Notice that Bonferroni narrower in
our example unless
![]() giving
giving 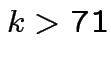 .
.
Motivations for ![]() :
:
1: Hypothesis
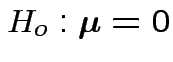 is true iff all
hypotheses
is true iff all
hypotheses
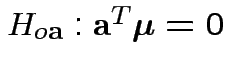 are true.
Natural test for
are true.
Natural test for
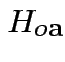 rejects if
rejects if
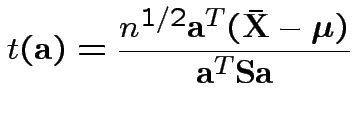
Fact:
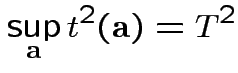
2: likelihood ratio method.
Compute
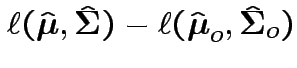
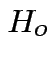 .
.
In our case to test
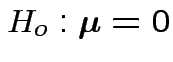 find
find
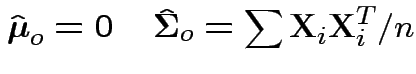
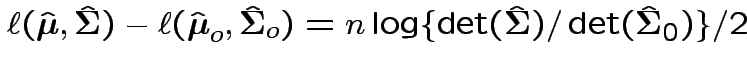
Now write
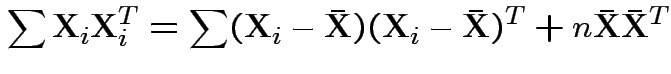
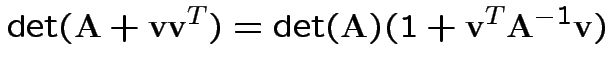
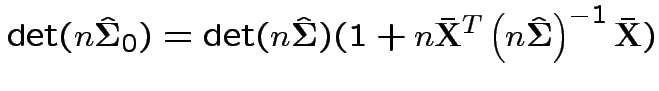
Again conclude: likelihood ratio test rejects for 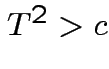 where
where ![]() chosen to make level
chosen to make level ![]() .
.
3: compare estimates of
![]() .
.
In univariate regression ![]() tests to compare a restricted model with a full model
have form
tests to compare a restricted model with a full model
have form
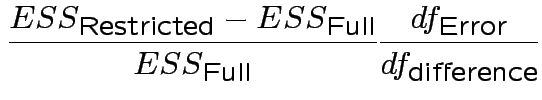

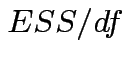 .
.
Here: substitute matrices.
Analogue of ESS for full model:
Analogue of ESS for reduced model:

In 1 sample example:
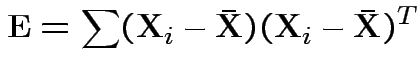
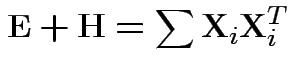
Test of
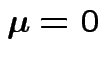 based on comparing
based on comparing
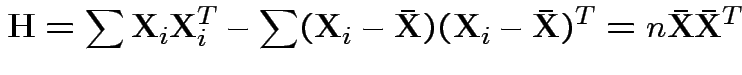
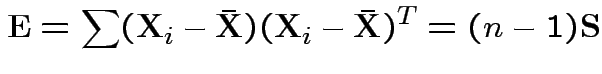
To make comparison. If null true
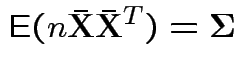
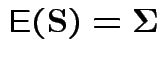
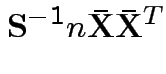
Measures of size based on eigenvalues of
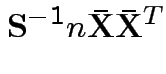
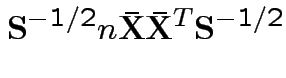
Suggested size measures for
 :
:
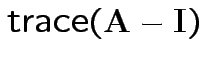 (= sum of eigenvalues).
(= sum of eigenvalues).
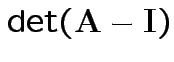 (= product of eigenvalues).
(= product of eigenvalues).
 .
.
For our matrix: eigenvalues all 0 except for one.
(So really-matrix not close to ![]() .)
.)
Largest eigenvalue is

But: see two sample problem for precise tests based on suggestions.
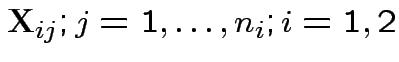 .
Model
.
Model
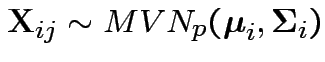 , independent.
, independent.
Test
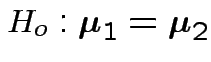 .
.
Case 1: for motivation only.
![]() known
known 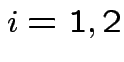 .
.
Natural test statistic: based on
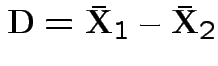
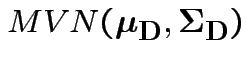 where
where
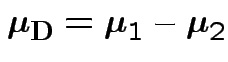
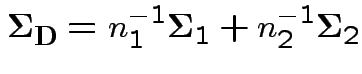

If
![]() not known must estimate. No universally
agreed best procedure (even for
not known must estimate. No universally
agreed best procedure (even for 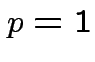 -- called Behrens-Fisher problem).
-- called Behrens-Fisher problem).
Usually: assume
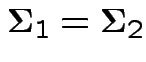 .
.
If so: MLE of
![]() is
is
![]() and of
and of
![]() is
is
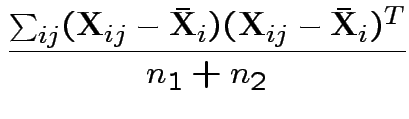
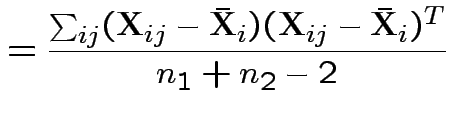
Possible test developments:
1) By analogy with 1 sample:
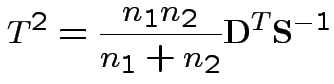 Pooled
Pooled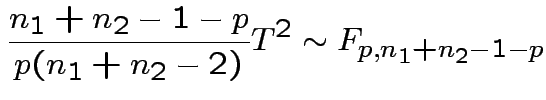
2) Union-intersection: test of
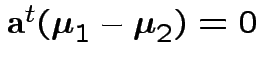 based on
based on

Get
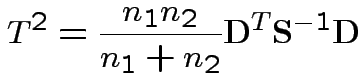
3) Likelihood ratio: the MLE of
![]() for the unrestricted model
is
for the unrestricted model
is
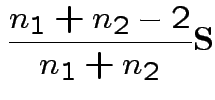
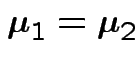 the mle of
the mle of
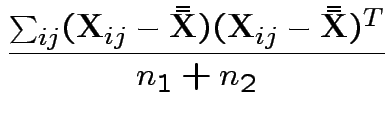

This simplifies to
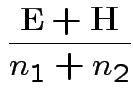
 Full
Full Restricted
Restricted
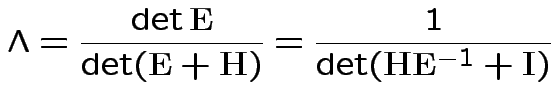
If ![]() are the eigenvalues of
are the eigenvalues of
![]() then
then
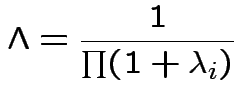
Two sample analysis in SAS on css network
data long;
infile 'tab57sh';
input group a b c;
run;
proc print;
run;
proc glm;
class group;
model a b c = group;
manova h=group / printh printe;
run;
Notes:
1) First 4 lines form DATA step:
a) creates data set named long by reading in 4 columns of data from file named tab57sh stored in same directory as I was in when I typed sas.
b) Calls variables group (=1 or 2 as label for the two groups) and a, b, c which are names for the 3 test scores for each subject.
2) Next two lines: print out data: result is (slightly edited)
Obs group a b c
1 1 19 20 18
2 1 20 21 19
3 1 19 22 22
etc till
11 2 15 17 15
12 2 13 14 14
13 2 14 16 13
3) Then use proc glm to do analysis:
a) class group declares that the variable group defines levels of a categorical variable.
b) model statement says to regress the variables a, b, c on variable group.
c) manova statement says to do both 3 univariate regressions
and a mulivariate regression and to print out the ![]() and
and ![]() matrices where
matrices where ![]() is the matrix corresponding to the presence
of the factor group in the model.
is the matrix corresponding to the presence
of the factor group in the model.
Output of MANOVA: First univariate results
The GLM Procedure
Class Level Information
Class Levels Values
group 2 1 2
Number of observations 13
Dependent Variable: a
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 1 54.276923 54.276923 19.38 0.0011
Error 11 30.800000 2.800000
Corrd Tot 12 85.076923
R-Square Coeff Var Root MSE a Mean
0.637975 10.21275 1.673320 16.38462
Source DF Type ISS Mean Square F Value Pr > F
group 1 54.276923 54.276923 19.38 0.0011
Source DF TypeIIISS Mean Square F Value Pr > F
group 1 54.276923 54.276923 19.38 0.0011
Dependent Variable: b
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 1 70.892308 70.892308 34.20 0.0001
Error 11 22.800000 2.072727
Corrd Tot 12 93.692308
Dependent Variable: c
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 1 94.77692 94.77692 39.64 <.0001
Error 11 26.30000 2.39090
Corrd Tot 12 121.07692
The matrices
E = Error SSCP Matrix
a b c
a 30.8 12.2 10.2
b 12.2 22.8 3.8
c 10.2 3.8 26.3
Partial Correlation Coefficients from
the Error SSCP Matrix / Prob > |r|
DF = 11 a b c
a 1.000000 0.460381 0.358383
0.1320 0.2527
b 0.460381 1.000000 0.155181
0.1320 0.6301
c 0.358383 0.155181 1.000000
0.2527 0.6301
H = Type III SSCP Matrix for group
a b c
a 54.276923077 62.030769231 71.723076923
b 62.030769231 70.892307692 81.969230769
c 71.723076923 81.969230769 94.776923077
The eigenvalues of
Characteristic Roots and Vectors of: E Inverse * H H = Type III SSCP Matrix for group E = Error SSCP Matrix Characteristic Characteristic Vector V'EV=1 Root Percent a b c 5.816159 100.00 0.00403434 0.12874606 0.13332232 0.000000 0.00 -0.09464169 -0.10311602 0.16080216 0.000000 0.00 -0.19278508 0.16868694 0.00000000 MANOVA Test Criteria and Exact F Statistics for the Hypothesis of No Overall group Effect H = Type III SSCP Matrix for group E = Error SSCP Matrix S=1 M=0.5 N=3.5 Statistic Value F NumDF DenDF Pr > F Wilks' Lambda 0.1467 17.45 3 9 0.0004 Pillai's Trace 0.8533 17.45 3 9 0.0004 Hotelling-Lawley Tr 5.8162 17.45 3 9 0.0004 Roy's Greatest Root 5.8162 17.45 3 9 0.0004Things to notice:
Wilk's Lambda:
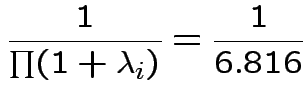
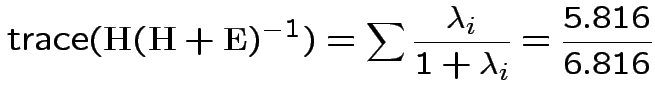
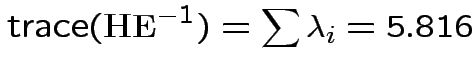
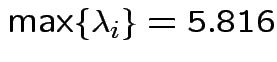
Data
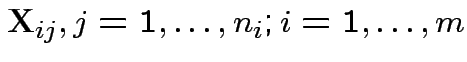 .
.
Model
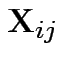 independent
independent
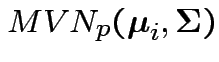 .
.
First problem of interest: test
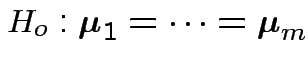
Based on ![]() and
and ![]() . MLE of
. MLE of
![]() is
is
![]() .
.
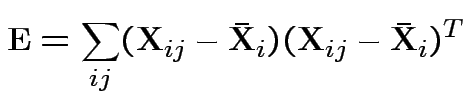
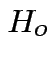 MLE of
MLE of
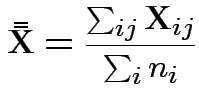
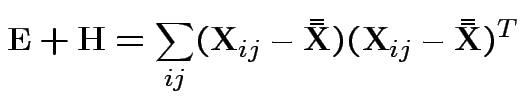
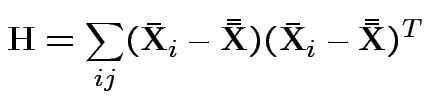
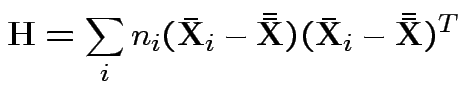
 .
The data
.
The data
1 19 20 18 1 20 21 19 1 19 22 22 1 18 19 21 1 16 18 20 1 17 22 19 1 20 19 20 1 15 19 19 2 12 14 12 2 15 15 17 2 15 17 15 2 13 14 14 2 14 16 13 3 15 14 17 3 13 14 15 3 12 15 15 3 12 13 13 4 8 9 10 4 10 10 12 4 11 10 10 4 11 7 12Code
data three;
infile 'tab57for3sams';
input group a b c;
run;
proc print;
run;
proc glm;
class group;
model a b c = group;
manova h=group / printh printe;
run;
data four;
infile 'table5.7';
input group a b c;
run;
proc print;
run;
proc glm;
class group;
model a b c = group;
manova h=group / printh printe;
run;
Pieces of output: first set of code does first 3 groups.
So: ![]() has rank 2.
has rank 2.
Characteristic Roots & Vectors of: E Inverse * H
Characteristic Characteristic Vector V'EV=1
Root Percent a b c
6.90568180 96.94 0.01115 0.14375 0.08795
0.21795125 3.06 -0.07763 -0.09587 0.16926
0.00000000 0.00 -0.18231 0.13542 0.02083
S=2 M=0 N=5
Statistic Value F NumDF Den DF Pr > F
Wilks' 0.1039 8.41 6 24 <.0001
Pillai's 1.0525 4.81 6 26 0.0020
Hotelling-Lawley 7.1236 13.79 6 14.353 <.0001
Roy's 6.9057 29.92 3 13 <.0001
NOTE: F Statistic for Roy's is an upper bound.
NOTE: F Statistic for Wilks'is exact.
Notice two eigenvalues not 0. Note that exact distribution
for Wilk's Lambda is available.
Now 4 groups
Root Percent a b c
15.3752900 98.30 0.01128 0.13817 0.08126
0.2307260 1.48 -0.04456 -0.09323 0.15451
0.0356937 0.23 -0.17289 0.09020 0.04777
S=3 M=-0.5 N=6.5
Statistic Value F NumDF Den DF Pr > F
Wilks' 0.04790913 10.12 9 36.657 <.0001
Pillai's 1.16086747 3.58 9 51 0.0016
Hot'ng-Lawley 15.64170973 25.02 9 20.608 <.0001
Roy's 15.37528995 87.13 3 17 <.0001
NOTE: F Statistic for Roy's is an upper bound.
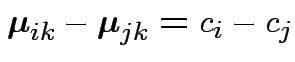
Test ?
Define
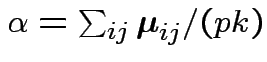 Then put
Then put
 |
||
 |
||
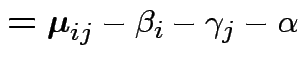 |
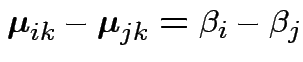
Data 
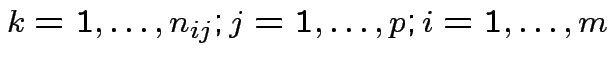 .
.
Model: independent,
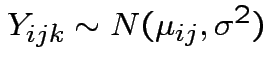 .
.
Note: this is the fixed effects model.
Usual approach: define grand mean, main effects, interactions:
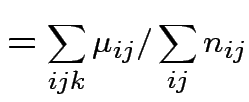 |
||
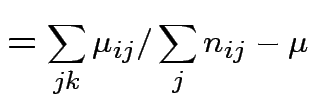 |
||
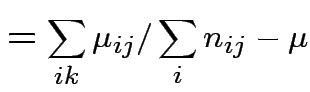 |
||
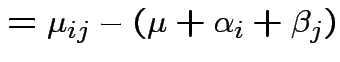 |
Test additive effects:
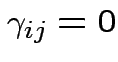 for all
for all  .
.
Usual test based on ANOVA:
Stack observations 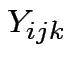 into vector
into vector ![]() , say.
, say.
Estimate ![]() ,
, ![]() , etc by least squares.
, etc by least squares.
Form vectors with entries ![]() ,
,
![]() etc.
etc.
Write

Fact: all vectors on RHS are independent and orthogonal. So:
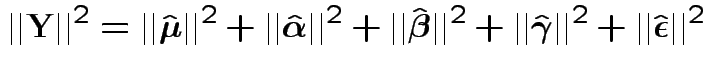
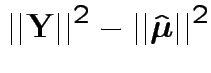
Our problem is like this one BUT the errors are not modeled as independent.
In the analogy:
![]() labels group.
labels group.
![]() labels the columns: ie
labels the columns: ie ![]() is a, b, c.
is a, b, c.
![]() runs from 1 to
runs from 1 to
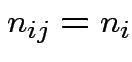 .
.
But

Now do analysis in SAS.
Tell SAS that the variables A, B and C are repeated measurements of the same quantity.
proc glm;
class group;
model a b c = group;
repeated scale;
run;
The results are as follows:
General Linear Models Procedure
Repeated Measures Analysis of Variance
Repeated Measures Level Information
Dependent Variable A B C
Level of SCALE 1 2 3
Manova Test Criteria and Exact F
Statistics for the Hypothesis of no
SCALE Effect
H = Type III SS&CP Matrix for SCALE
E = Error SS&CP Matrix
S=1 M=0 N=7
Statistic
Value F NumDF DenDF Pr > F
Wilks' Lambda 0.56373 6.1912 2 16 0.0102
Pillai's Trace 0.43627 6.1912 2 16 0.0102
Hotelling-Lawley 0.77390 6.1912 2 16 0.0102
Roy's 0.77390 6.1912 2 16 0.0102
Note: should look at interactions first.
Manova Test Criteria and F Approximations
for the Hypothesis of no SCALE*GROUP Effect
S=2 M=0 N=7
Statistic Value F NumDF DenDF Pr > F
Wilks' Lambda 0.56333 1.7725 6 32 0.1364
Pillai's Trace 0.48726 1.8253 6 34 0.1234
Hotelling-Lawley 0.68534 1.7134 6 30 0.1522
Roy's 0.50885 2.8835 3 17 0.0662
NOTE: F Statistic for Roy's Greatest
Root is an upper bound.
NOTE: F Statistic for Wilks' Lambda is exact.
Repeated Measures Analysis of Variance
Tests of Hypotheses for Between Subjects Effects
Source DF Type III SS Mean Square F Pr > F
GROUP 3 743.900000 247.966667 70.93 0.0001
Error 17 59.433333 3.496078
Repeated Measures Analysis of Variance
Univariate Tests of Hypotheses for
Within Subject Effects
Source: SCALE Adj Pr > F
DF TypeIIISS MS F Pr > F G - G H - F
2 16.624 8.312 5.39 0.0093 0.0101 0.0093
Source: SCALE*GROUP
DF TypeIII MS F Pr > F G - G H - F
6 18.9619 3.160 2.05 0.0860 0.0889 0.0860
Source: Error(SCALE)
DF TypeIII SS Mean Square
34 52.4667 1.54313725
Greenhouse-Geisser Epsilon = 0.9664
Huynh-Feldt Epsilon = 1.2806
Greenhouse-Geisser, Huynh-Feldt test to see if
Return to 2 way anova model. Express as:
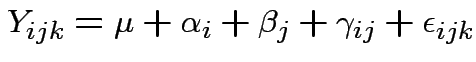
For fixed effects model is
 iid
iid
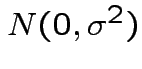 .
.
For MANOVA model vector of
 is MVN but
with covariance as for
is MVN but
with covariance as for ![]() .
.
Intermediate model. Put in subject effect.
Assume
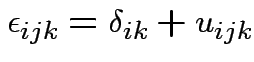
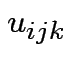 iid
iid
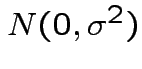 and
and
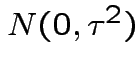 . Then
. Then
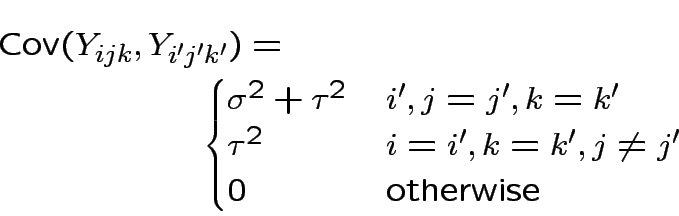
Essentially model says
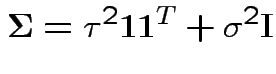
Do univariate anova: The data reordered:
1 1 1 19 1 1 2 20 1 1 3 18 2 1 1 20 2 1 2 21 2 1 3 19 et cetera 2 4 2 10 2 4 3 12 3 4 1 11 3 4 2 10 3 4 3 10 4 4 1 11 4 4 2 7 4 4 3 12The four columns are now labels for subject number, group, scale (a, b or c) and the response. The sas commands:
data long;
infile 'table5.7uni';
input subject group scale score;
run;
proc print;
run;
proc glm;
class group;
class scale;
class subject;
model score =group subject(group)
scale group*scale;
random subject(group) ;
run;
Some of the output:
Dependent Variable: SCORE
Sum of Mean
Source DF Squares Square F Pr > F
Model 28 843.5333 30.126 19.52 0.0001
Error 34 52.4667 1.543
Total 62 896.0000
Root MSE SCORE Mean
1.242231 15.33333
Source DF TypeISS MS F Pr > F
GROUP 3 743.9000 247.9667 160.69 0.0001
SUBJECT(GROUP) 17 59.4333 3.4961 2.27 0.0208
SCALE 2 21.2381 10.6190 6.88 0.0031
GROUP*SCALE 6 18.9620 3.1603 2.05 0.0860
Source DF TypeIIISS MS F Pr > F
GROUP 3 743.9000 247.9667 160.69 0.0001
SUBJECT(GROUP) 17 59.4333 3.4961 2.27 0.0208
SCALE 2 16.6242 8.3121 5.39 0.0093
GROUP*SCALE 6 18.9619 3.1603 2.05 0.0860
Source Type III Expected Mean Square
GROUP Var(Error) + 3 Var(SUBJECT(GROUP))
+ Q(GROUP,GROUP*SCALE)
SUBJECT(GROUP) Var(Error) + 3 Var(SUBJECT(GROUP))
SCALE Var(Error) + Q(SCALE,GROUP*SCALE)
GROUP*SCALE Var(Error) + Q(GROUP*SCALE)
Type I Sums of Squares:
Type III Sums of Squares:
Notice hypothesis of no group by scale interaction is acceptable.
Under the assumption of no such group by scale interaction the hypothesis of no group effect is tested by dividing group ms by subject(group) ms.
Value is 70.9 on 3,17 degrees of freedom.
This is NOT the F value in the table above since the table above is for FIXED effects.
Notice that the sums of squares in this table match those produced in the repeated measures ANOVA. This is not accidental.
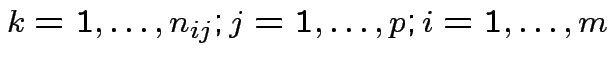 .
.
Model: independent,
 .
.
Note: fixed effects model.
Usual approach: define grand mean, main effects, interactions:
 |
||
 |
||
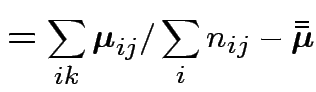 |
||
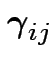 |
 |
Test additive effects:
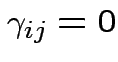 for all
for all 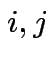 .
.
Exactly parallel to univariate 2 way ANOVA:
Estimate ![]() ,
, ![]() , etc by least squares.
, etc by least squares.
Formulas exactly like univariate.
Form vectors with entries ![]() ,
,
![]() etc.
etc.
Write

This defines the matrix of fitted residuals
![]() .
.
Fact:
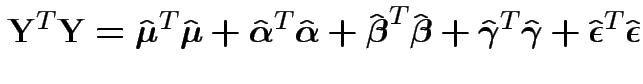
Also
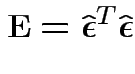
The SAS commands for a two way analysis of variance with 3 response variables.
data mas;
infile 'mas';
input row column y1 y2 y3;
proc print;
proc glm;
class row column;
model y1-y3 = row | column;
manova h=_all_ / printh printe;
run;
Features of the code:
OBS ROW COLUMN Y1 Y2 Y3 1 1 1 18.2 16.5 0.2 2 1 1 18.7 19.5 0.3 3 1 1 19.5 19.8 0.2 4 1 2 19.2 19.5 0.2 5 1 2 18.4 19.8 0.2 6 1 2 20.7 19.4 0.2 7 2 1 21.3 23.3 0.3 8 2 1 19.6 22.3 0.5 9 2 1 20.2 19.0 0.4 10 2 2 18.9 22.0 0.3 11 2 2 20.7 21.1 0.2 12 2 2 21.6 20.3 0.2 13 3 1 20.7 16.7 0.3 14 3 1 21.0 19.3 0.4 15 3 1 17.2 15.9 0.3 16 3 2 20.2 19.0 0.2 17 3 2 18.4 17.9 0.3 18 3 2 20.9 19.9 0.2Here is the matrix
Error SS&CP Matrix
Y1 Y2 Y3
Y1 21.106667 8.783333 -0.336667
Y2 8.783333 26.646667 0.173333
Y3 -0.336667 0.173333 0.046667
and the matrix used to test the hypothesis of no
interactions, that is,
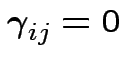 for all
for all
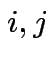 :
:
H = Type III SS&CP Matrix for ROW*COLUMN
Y1 Y2 Y3
Y1 0.28778 0.435 0.06
Y2 0.435 3.2233 0.13667
Y3 0.06 0.13667 0.01333
This leads to the test statistics:
S=2 M=0 N=4 Statistic Value F NumDF DenDF Pr > F Wilks' 0.6576 0.7771 6 20 0.5973 Pillai's 0.3673 0.8249 6 22 0.5629 Hot'g-L'y 0.4827 0.7241 6 18 0.6359 Roy's 0.3839 1.4077 3 11 0.2926Conclusion: there is no evidence that interaction terms are needed. In other words the effect of changing the level of the row variable does not depend on the level of the column variable, and vice versa.
No interaction:
investigate main effects.
H = Type III SS&CP Matrix for COLUMN
Y1 Y2 Y3
Y1 0.37556 0.9533 -0.13
Y2 0.95333 2.42 -0.33
Y3 -0.13 -0.33 0.045
S=1 M=0.5 N=4
Statistic Value F NumDF DenDF Pr > F
Wilks' 0.41672 4.6656 3 10 0.0275
Pillai's 0.58328 4.6656 3 10 0.0275
Hot'g-L'y 1.39968 4.6656 3 10 0.0275
Roy's 1.39968 4.6656 3 10 0.0275
H = Type III SS&CP Matrix for ROW
Y1 Y2 Y3
Y1 4.8144 8.68944 0.37889
Y2 8.6894 32.68778 0.53556
Y3 0.3789 0.53556 0.03111
S=2 M=0 N=4
Statistic Value F NumDF DenDF Pr>F
Wilks' 0.2144 3.8652 6 20 0.0101
Pillai's 1.0680 4.2019 6 22 0.0058
Hot'g-L'y 2.3465 3.5198 6 18 0.0175
Roy's 1.4169 5.1953 3 11 0.0177
Conclusions: both row and column effects appear to exist.
Rerun model without interactions.
Common tactic to increase degrees of freedom for estimation of error variance.
data mas;
infile 'mas';
input row column y1 y2 y3;
proc print;
proc glm;
class row column;
model y1-y3 = row column;
manova h=_all_ / printh printe;
run;
Notice absence of | which means no interaction
included in model.
Effect: only ![]() changed. Pool
changed. Pool ![]() above with
above with ![]() for
interaction.
for
interaction.
E = Error SSCP Matrix
y1 y2 y3
y1 21.39444 9.21833 -0.27667
y2 9.21833 29.87 0.31
y3 -0.27667 0.31 0.06
H = Type III SSCP Matrix for row
E = Error SSCP Matrix
S=2 M=0 N=5
Statistic Value F NumDF DenDF Pr > F
Wilks' 0.2630 3.80 6 24 0.0084
Pillai's 0.9700 4.08 6 26 0.0052
Hot'g-Lawley 1.9162 3.71 6 14.353 0.0195
Roy's 1.1377 4.93 3 13 0.0168
Compare:
![$\displaystyle \left[\begin{array}{rrr}
21.39 & 9.22 & -0.28
\\
9.22 & 29.87 & 0.31
\\
-0.28 & 0.31 & 0.06
\end{array}\right] =
$](img246.gif)
![$\displaystyle \left[\begin{array}{rrr}
0.29 & 0.44 & 0.06
\\
0.44 & 3.22 & 0....
...8& -0.34
\\
8.78 & 26.65 & 0.17
\\
-0.34 & 0.17 & 0.05
\end{array}\right]
$](img247.gif)
1) In 1 way manova there is a likelihood ratio test for the hypothesis of
homogeneous variances against the alternative of a different
![]() in
each group.
in
each group.
2) Univariate analyses have advantage of increased power; price is increased assumptions.
3) In SAS proc glm the statements means may be used to generate multiple comparisons procedures. SAS implements many such (Bonferroni, Scheffé, Tukey, ...
4) The random statement causes production of a table of expected mean squares.
Plot variable mean versus variable level for each group.
Put group mean vectors in rows of 4![]() 3 matrix tab5.7means then:
3 matrix tab5.7means then:
plot(c(1,1,1,1,2,2,2,2,3,3,3,3),tab5.7means,
type='n',xaxt='n',xlab="",ylab="Mean")
lines(1:3,tab5.7means[1,])
lines(1:3,tab5.7means[2,])
lines(1:3,tab5.7means[3,])
lines(1:3,tab5.7means[4,])
axis(side=1,at=1:3,labels=c("A","B","C"))
If accepted use same output to test no group effect.
Recall output from SAS
Univariate Tests of Hypotheses for
Within Subject Effects
Source: SCALE*GROUP
DF TypeIII MS F Pr > F G - G H - F
6 18.9619 3.160 2.05 0.0860 0.0889 0.0860
As before: weak evidence of non-parallel profiles. Notice
adjustments in univariate test designed to improve Test for no group effect assuming no interaction: model is
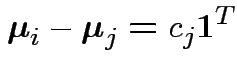
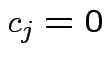 .
.
Repeated Measures Analysis of Variance Tests of Hypotheses: Between Subjects Effects Source DF Type III SS Mean Square F Pr > F GROUP 3 743.900000 247.966667 70.93 0.0001 Error 17 59.433333 3.496078
New data set (to match sas total variables, divide by 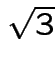 :
:
1 32.908965343808667 1 34.641016151377542 1 36.373066958946424 1 33.48631561299829 et cetera 4 18.475208614068023 4 17.897858344878397 4 17.320508075688771Sas code:
data profile;
infile 'prof.dat';
input group average;
run;
proc glm;
class group;
model average = group;
run;
This gives the output
Dependent Variable: average
Sum of
Source DF Squares Mean Sq F Pr > F
Model 3 743.90 247.9667 70.93 <.0001
Error 17 59.43 3.4961
Corrd Tot 20 803.33
Notice agreement with SAS output.
Conclusion: profiles are credibly parallel in the 4 groups
but not co-incident. Notice small sample size. Had they
been co-incident we might test hypothesis of constant profiles:
no scale effect.