Principal components

Suppose ${\bf Y}\sim MVN_p({\boldsymbol\mu},{\boldsymbol\Sigma})$. Idea: study structure of ${\boldsymbol\Sigma}$ or of $R$, the correlation matrix derived from ${\boldsymbol\Sigma}$.

Which linear combination of the entries of ${\bf Y}$ has maximal variance?

None: variance of ${\bf a}^T{\bf Y}$ is ${\bf a}^T{\bf Y}{\bf a}$ which is proportional to squared length of $\bf a$.

So: maximize

$$\frac{{\bf a}^T{\boldsymbol\Sigma}{\bf a}}{{\bf a}^T{\bf a}}$$

Solution is $\bf a$ is eigenvector of ${\boldsymbol\Sigma}$ corresponding to largest eigenvalue of ${\boldsymbol\Sigma}$.

Now: find another linear combination which is independent of first and maximizes variance (divided by ${\bf a}^T{\bf a}$).

Principal Components: Find 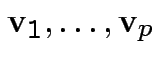${\bf v}_1,\ldots,{\bf v}_p$ which are orthonormal eigenvectors of ${\boldsymbol\Sigma}$. Let $\lambda_i$, $i=1,\ldots,p$ be the corresponding eigenvalues. We call ${\bf v}_1^T{\bf Y},\ldots,{\bf v}_p^T{\bf Y}$ the principal components of ${\bf Y}$.

If ${\bf P}$ has columns ${\bf v}_i$ then ${\bf P}^T{\bf Y}$ has a MVN $_p(0, \boldsymbol\Lambda)$ where $\boldsymbol\Lambda$ is diagonal matrix of eigenvalues.

Columns of ${\bf P}{\bf Y}$ are the components.

We can reconstruct the original ${\bf Y}$ from the components ${\bf v}_1^T{\bf Y},\ldots,{\bf v}_p^T{\bf Y}$ because

$${\bf Y}= {\bf P}{\bf P}^T{\bf Y}$$

or

$${\bf Y}= \sum \left({\bf v}_i^T{\bf Y}\right){\bf v}_i$$

Points to ponder:

1: Principal component $i$ has variance $\lambda_i$.

2: Can compare $\lambda_i$ to $\sum_i \lambda_i = {\rm trace}({\boldsymbol\Sigma})$.

3: Try to interpret components; often leading component is some sort of average then others are contrasts.

4: To estimate replace ${\boldsymbol\Sigma}$ by ${\bf S}$.

5: Process can be done on original ${\bf Y}$ or on standardized variates:

$$X_i = (Y_i -\mu_i)/\sqrt{\Sigma_{ii}}$$

Covariance matrix of $X_i$ is ${\bf R}$, correlation matrix.

6: General advice: use ${\bf S}$ when different variables in $Y$ are commensurate (same units, comparable). Use ${\bf R}$ otherwise.

Principal Components example

Data: Table 9.12 in Johnson and Wichern.

3 measurements on sales performance and 4 test scorese for 50 salespeople in large firm. The data begin

Growth	Profit	New	Creat	Mech	Abst	Math
93.0	96.0	97.8	9	12	9	20
88.8	91.8	96.8	7	10	10	15
95.0	100.3	99.0	8	12	9	26

PCA on ${\bf S}$

Read in and print out the data.

> sales <- matrix(scan("T9-12.DAT"),ncol=7,byrow=T)
> sales
       [,1]  [,2]  [,3] [,4] [,5] [,6] [,7]
 [1,]  93.0  96.0  97.8    9   12    9   20
 [2,]  88.8  91.8  96.8    7   10   10   15
 [3,]  95.0 100.3  99.0    8   12    9   26

Compute the variance covariance matrix and the correlation matrix and print them out.

> S <- var(sales)
> S
53.837  68.794 30.564 16.580 17.585 10.588  71.699
68.794 102.502 40.195 21.656 25.561 10.081 100.744
30.565  40.195 22.205 13.037 10.168  6.464  42.335
16.580  21.656 13.037 15.604  7.898  1.242  17.176
17.585  25.561 10.168  7.898 11.457  2.795  20.493
10.588  10.081  6.464  1.242  2.795  4.578  12.770
71.698 100.744 42.335 17.176 20.493 12.770 111.043
> D <- diag(sqrt(diag(S)))
> D
7.33735  0.0000 0.0000 0.0000 0.0000 0.0000  0.0000
0.00000 10.1243 0.0000 0.0000 0.0000 0.0000  0.0000
0.00000  0.0000 4.7122 0.0000 0.0000 0.0000  0.0000
0.00000  0.0000 0.0000 3.9502 0.0000 0.0000  0.0000
0.00000  0.0000 0.0000 0.0000 3.3848 0.0000  0.0000
0.00000  0.0000 0.0000 0.0000 0.0000 2.1396  0.0000
0.00000  0.0000 0.0000 0.0000 0.0000 0.0000 10.5377
> R <- solve(D,S)%*% solve(D)

> R
1.0000 0.9261 0.8840 0.5720 0.7081 0.6741 0.9273
0.9261 1.0000 0.8425 0.5415 0.7459 0.4654 0.9443
0.8840 0.8425 1.0000 0.7004 0.6375 0.6411 0.8526
0.5720 0.5415 0.7004 1.0000 0.5907 0.1469 0.4126
0.7081 0.7459 0.6375 0.5907 1.0000 0.3860 0.5746
0.6744 0.4654 0.6411 0.1469 0.3860 1.0000 0.5664
0.9273 0.9443 0.8526 0.4126 0.5746 0.5664 1.0000
> round(R,2)
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 1.00 0.93 0.88 0.57 0.71 0.67 0.93
[2,] 0.93 1.00 0.84 0.54 0.75 0.47 0.94
[3,] 0.88 0.84 1.00 0.70 0.64 0.64 0.85
[4,] 0.57 0.54 0.70 1.00 0.59 0.15 0.41
[5,] 0.71 0.75 0.64 0.59 1.00 0.39 0.57
[6,] 0.67 0.47 0.64 0.15 0.39 1.00 0.57
[7,] 0.93 0.94 0.85 0.41 0.57 0.57 1.00

Correlations between three measures of sales performance - all quite high.

Also very high: correlation of math score with the three sales performance indices.

I find it interesting that the correlations amongst the 4 test scores are not all that high.

Compute eigenvalues and eigenvectors of $S$.

Note: without symmetric=T argument to eigen might not get normalized eigenvectors.

> e.S <- eigen(S,symmetric=T)
> e.S
$values:
[1] 285.1366314  17.2678388   8.9785502   5.8957342   
               2.5247046   1.1505297
[7]   0.2710316

$vectors:
   [,1]     [,2]    [,3]     [,4]     [,5]     [,6]
 0.42055 -0.12038 -0.31712 -0.47136  0.59884  0.05743
 0.58892 -0.06545  0.59396  0.07524 -0.05950  0.53029
 0.25070 -0.25607 -0.46093  0.16111 -0.62886  0.17742
 0.12864 -0.73755 -0.15906  0.41980  0.25206 -0.14283
 0.14144 -0.36484  0.36098 -0.52253 -0.34536 -0.56932
 0.07253  0.05320 -0.38705 -0.47051 -0.24056  0.30162
 0.60962  0.48553 -0.16961  0.27486 -0.04146 -0.49852
      [,7]
  0.35212680
 -0.07541783
  0.45411767
 -0.39244052
  0.01215659
 -0.68693393
 -0.19509084

Store the eigenvectors in $P$ and check that $PP^t=I$.

> P.S <- e.S$vectors
> P.S %*% t(P.S)
    [,1]       [,2]       [,3]       [,4]        [,5]
 1.000e+00  3.990e-16  8.327e-17  3.886e-16 -5.117e-17
 3.990e-16  1.000e+00 -6.939e-18  1.492e-16  1.315e-16
 8.327e-17 -6.939e-18  1.000e+00  3.886e-16 -1.830e-16
 3.886e-16  1.492e-16  3.886e-16  1.000e+00  3.452e-16
-5.117e-17  1.315e-16 -1.830e-16  3.452e-16  1.000e+00
-9.159e-16  3.053e-16  0.000e+00 -5.551e-17 -3.036e-16
 1.804e-16 -1.006e-16  2.776e-17 -3.608e-16 -1.518e-17
              [,6]          [,7]
[1,] -9.159340e-16  1.804112e-16
[2,]  3.053113e-16 -1.006140e-16
[3,]  0.000000e+00  2.775558e-17
[4,] -5.551115e-17 -3.608225e-16
[5,] -3.035766e-16 -1.517883e-17
[6,]  1.000000e+00 -5.551115e-17
[7,] -5.551115e-17  1.000000e+00
> round(.Last.value,6)
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    1    0    0    0    0    0    0
[2,]    0    1    0    0    0    0    0
[3,]    0    0    1    0    0    0    0
[4,]    0    0    0    1    0    0    0
[5,]    0    0    0    0    1    0    0
[6,]    0    0    0    0    0    1    0
[7,]    0    0    0    0    0    0    1

Put eigenvalues in diagonal matrix $\Lambda$ (here L).

> L.S <- diag(e.S$values)
> L.S
   [,1]    [,2]    [,3]  [,4]   [,5]   [,6]   [,7]
 285.137  0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
   0.000 17.2678 0.0000 0.0000 0.0000 0.0000 0.0000
   0.000  0.0000 8.9786 0.0000 0.0000 0.0000 0.0000
   0.000  0.0000 0.0000 5.8957 0.0000 0.0000 0.0000
   0.000  0.0000 0.0000 0.0000 2.5247 0.0000 0.0000
   0.000  0.0000 0.0000 0.0000 0.0000 1.1505 0.0000
   0.000  0.0000 0.0000 0.0000 0.0000 0.0000 0.2710

Check the identity $S=P\Lambda P^t$

> P.S%*% L.S %*% t(P.S) - S
     [,1]       [,2]       [,3]       [,4]       [,5]
 -2.132e-14 -2.842e-14 -1.066e-14  1.421e-14 -3.553e-15
 -2.842e-14 -9.948e-14 -3.553e-14  3.553e-15 -1.421e-14
 -7.105e-15 -2.842e-14 -7.105e-15  1.243e-14 -5.329e-15
  1.776e-14  7.105e-15  1.243e-14  1.243e-14  8.882e-15
 -3.553e-15 -1.421e-14 -3.553e-15  8.882e-15 -7.105e-15
 -8.527e-14 -7.816e-14 -4.263e-14 -9.992e-15 -2.753e-14
  2.842e-14 -2.842e-14  0.000e+00  3.553e-15 -3.553e-15
              [,6]          [,7]
 -8.348877e-14  1.421085e-14
 -7.815970e-14 -4.263256e-14
 -4.263256e-14  0.000000e+00
 -9.992007e-15  3.552714e-15
 -2.664535e-14  0.000000e+00
 -5.240253e-14 -3.907985e-14
 -3.730349e-14  5.684342e-14

Watch what happens if you don't use symmetric=T.

> e.R <- eigen(R)
> e.R
$values:
[1] 5.03459779 0.93351614 0.49791975 
    0.42124549 0.08104043 0.02034063
   0.01133977
$vectors:
  et cetera
> P.R <- e.R$vectors
> P.R %*% t(P.R)
  [,1]   [,2]   [,3]    [,4]  [,5]    [,6]    [,7]
 1.3135 0.3704 0.1903  0.3166 0.2481  0.3133 0.3503
 0.3704 1.0729 0.3820  0.2968 0.3079  0.2920 0.3169
 0.1903 0.3820 1.3334  0.1737 0.3199  0.1931 0.3926
 0.3166 0.2968 0.1737  1.0804 0.2238 -0.0134 0.2442
 0.2481 0.3079 0.3199  0.2238 1.1357  0.1553 0.2502
 0.3133 0.2920 0.1931 -0.0134 0.1553  0.9978 0.3284
 0.3503 0.3169 0.3926  0.2442 0.2502  0.3284 1.0804

This should have been the identity but isn't.

Now make a plot of the first principal component versus the second.

> Y.S <- sales %*% P.S
> postscript("prcmps_S.ps",horizontal=F)
> plot(Y.S[,1],Y.S[,2],xlab="First PC",
   ylab="Second PC",main="Plot of 1st
vs 2nd PC\n us ing S")
> dev.off()
Generated postscript file "prcmps_S.ps".

Now try to interpret the eigenvectors

> P.S
 [,1]    [,2]    [,3]    [,4]    [,5]    [,6]
0.4206 -0.1204 -0.3171 -0.4714  0.5988  0.0574
0.5889 -0.0654  0.5940  0.0752 -0.0595  0.5309
0.2507 -0.2561 -0.4609  0.1611 -0.6289  0.1774
0.1286 -0.7375 -0.1591  0.4198  0.2521 -0.1428
0.1414 -0.3648  0.3610 -0.5225 -0.3454 -0.5693
0.0725  0.0532 -0.3871 -0.4705 -0.2406  0.3016
0.6096  0.4855 -0.1696  0.2749 -0.0415 -0.4985
       [,7]
  0.35212680
 -0.07541783
  0.45411767
 -0.39244052
  0.01215659
 -0.68693393
 -0.19509084

Leading principal component: used first column of $P$ as coefficients.

Hard to interpret although all the weights are positive.

Big weights on components with large variances which is natural but uninformative.

The trouble is that the 7 variables are not all really comparable.

Do whole thing again with $R$.

> e.R <- eigen(R,symmetric=T)
> e.R
$values:
[1] 5.03459779 0.93351614 0.49791975 
    0.42124549 0.08104043 0.02034063
    0.01133977
$vectors:
  [,1]    [,2]    [,3]   [,4]     [,5]    [,6]
 0.4337  0.1118 -0.0755  0.0424 -0.6325 -0.3366
 0.4202 -0.0293 -0.4425 -0.0108  0.0001  0.7853
 0.4211 -0.0092  0.2042  0.3249  0.7010 -0.1568
 0.2943 -0.6684  0.4515  0.3027 -0.2610  0.1142
 0.3491 -0.2950  0.0059 -0.8466  0.1742 -0.1970
 0.2892  0.6424  0.6038 -0.1537 -0.0870  0.2363
 0.4074  0.2004 -0.4340  0.2460  0.0496 -0.3711
            [,7]
[1,]  0.52782527
[2,]  0.09948330
[3,]  0.39916419
[4,] -0.29995962
[5,] -0.07231139
[6,] -0.22844351
[7,] -0.63622351
> P.R <- e.R$vectors
> L.R <- diag(e.R$values)
> L.R
     [,1]  [,2]  [,3]  [,4]   [,5]  [,6] [,7]
[1,] 5.035 0.000 0.000 0.000 0.000 0.000 0.000
[2,] 0.000 0.934 0.000 0.000 0.000 0.000 0.000
[3,] 0.000 0.000 0.498 0.000 0.000 0.000 0.000
[4,] 0.000 0.000 0.000 0.421 0.000 0.000 0.000
[5,] 0.000 0.000 0.000 0.000 0.081 0.000 0.000
[6,] 0.000 0.000 0.000 0.000 0.000 0.020 0.000
[7,] 0.000 0.000 0.000 0.000 0.000 0.000 0.011

Try to interpret eigenvectors of ${\bf R}$.

> P.R
 [,1]   [,2]    [,3]  [,4]   [,5]    [,6]
 0.433  0.112 -0.075  0.042 -0.632 -0.337
 0.420 -0.029 -0.442 -0.011  0.000  0.785
 0.421 -0.009  0.204  0.325  0.701 -0.157
 0.294 -0.668  0.451  0.303 -0.261  0.114
 0.349 -0.295  0.006 -0.847  0.174 -0.197
 0.289  0.642  0.604 -0.154 -0.087  0.236
 0.407  0.200 -0.434  0.246  0.050 -0.371
            [,7]
[1,]  0.52782527
[2,]  0.09948330
[3,]  0.39916419
[4,] -0.29995962
[5,] -0.07231139
[6,] -0.22844351
[7,] -0.63622351

Entries in first column nearly constant: leading principal component is close to just being average of 7 variables, each expressed in standard units ( $(X-\bar X) /s$).

Next principal component is essentially a weighted average of Mathematics and Abstract Reasoning minus a similar average of Mechanical reasoning and Creativity.

The third PC seems hard to interpret.

Now transform the data to get the principal components $(I-n^{-1}11^t)XP$. Then plot the first two principal components against each other and examine the plot looking for interesting cases.

> postscript("prcmps_R.ps", horizontal = F)
> plot(Y.R[, 1], Y.R[, 2], xlab = "First PC", 
           ylab = "Second PC", main =
        "Plot of 1st vs 2nd PC\n using R")
> l1 <- (abs(Y.R[,1])>25)
> l1
 [1] F F F F F F F T F F F F F F F T F F F 
     F F F F F F F F F F F F F F F F F F F
     F F F F F T F F F T F F
> l2 <- (abs(Y.R[,2]) > 6)
> l2
 [1] F F F F F F F F F F F F F F F F F F F 
     F F T F F F F F F F F F T F F F T T F
     F F F T F F F F F F F F
> l3 <- (l1|l2)
> l3
 [1] F F F F F F F T F F F F F F F T F F F 
     F F T F F F F F F F F F T F F F T T F
     F F F T F T F F F T F F
> text(Y.R[,1],Y.R[,2],labels=l3)
> dev.off()
Generated postscript file "prcmps_R.ps".
 null device
           1

Here is the plot.