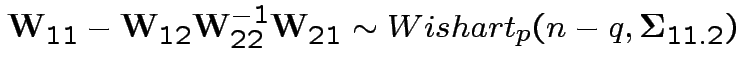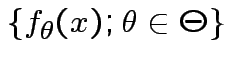 :
:
Given data ![]() with model
with model
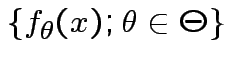 :
:
Definition: The likelihood function is map ![]() : domain
: domain
![]() , values given by
, values given by
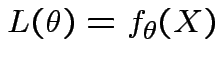
Key Point: think about how the density depends on ![]() not
about how it depends on
not
about how it depends on ![]() .
.
Notice: ![]() , observed value of the
data, has been plugged into the formula for density.
, observed value of the
data, has been plugged into the formula for density.
We use likelihood for most inference problems:
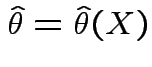 which lies in
which lies in 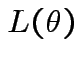 over
over
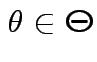 if such a
if such a
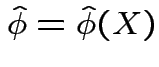 of
of
 . We use
. We use
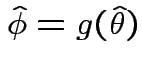 where
where
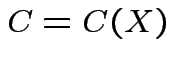 in
in
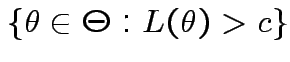
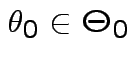 where
where
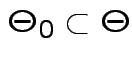 . We base our
decision
on the likelihood ratio
. We base our
decision
on the likelihood ratio
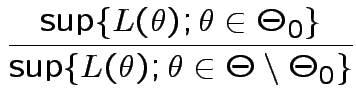
Maximum Likelihood Estimation
To find MLE maximize ![]() .
.
Typical function maximization problem:
Set gradient of ![]() equal to 0
equal to 0
Check root is maximum, not minimum or saddle point.
Often ![]() is product of
is product of ![]() terms (given
terms (given ![]() independent observations).
independent observations).
Much easier to work with logarithm
of ![]() : log of product is sum and logarithm is monotone
increasing.
: log of product is sum and logarithm is monotone
increasing.
Definition: The Log Likelihood function is
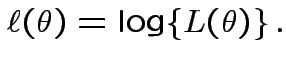
Simplest problem: collect replicate measurements
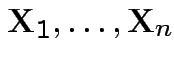 from single population.
from single population.
Model: ![]() are iid
are iid
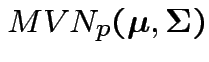 .
.
Parameters (![]() ):
):
 .
Parameter space:
.
Parameter space:
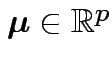 and
and
![]() is some positive definite
is some positive definite 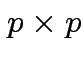 matrix.
matrix.
Log likelihood is
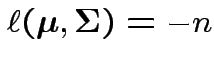 |
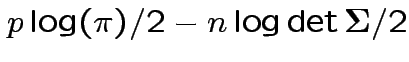 |
|
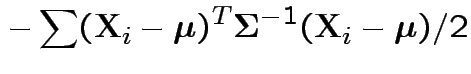 |
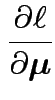 |
 |
|
 |
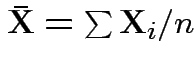 .
Second derivative wrt
.
Second derivative wrt
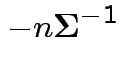
Fact: if second derivative matrix is negative definite everywhere then function is concave; no more than 1 critical point.
Summary: ![]() is maximized at
is maximized at
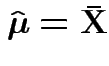
More difficult: differentiate ![]() wrt
wrt
![]() .
.
Somewhat simpler: set
![]()
First derivative wrt ![]() is matrix with entries
is matrix with entries
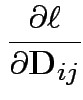
Need: derivative of two functions:
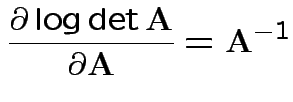
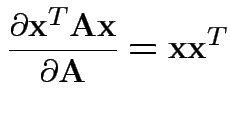
Fact:
![]() th entry of
th entry of
![]() is
is
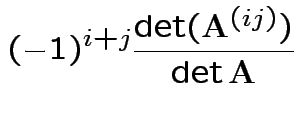
Fact:
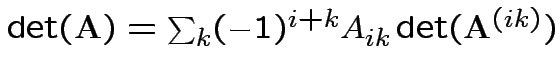 ; expansion
by minors.
; expansion
by minors.
Conclusion
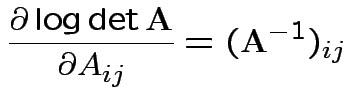
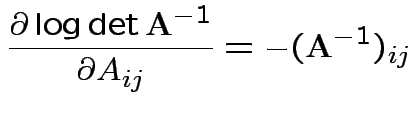
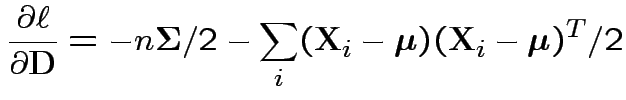
Set = 0 and find only critical point is
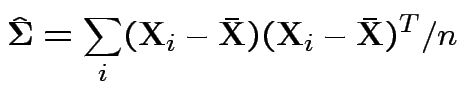
Usual sample covariance matrix is

Properties of MLEs:
1)
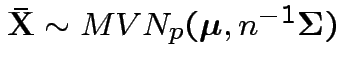
2)
 .
.
Distribution of ![]() ? Joint distribution of
? Joint distribution of
![]() and
and ![]() ?
?
Theorem:
Suppose
 are independent
are independent
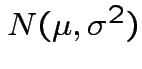 random
variables.
Then
random
variables.
Then
 .
.
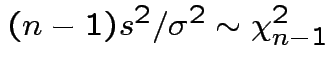 .
.
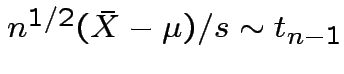 .
.
Proof: Let
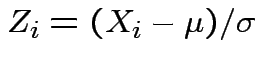 .
.
Then
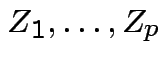 are
independent
are
independent 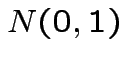 .
.
So
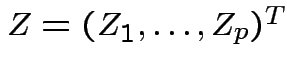 is multivariate
standard normal.
is multivariate
standard normal.
Note that
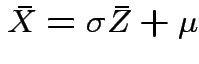 and
and
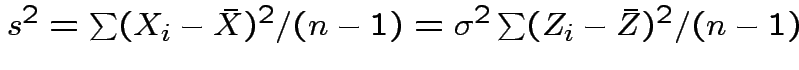 Thus
Thus
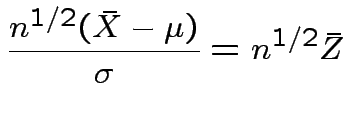
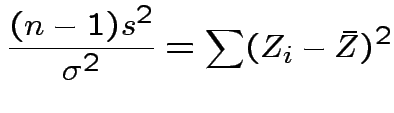
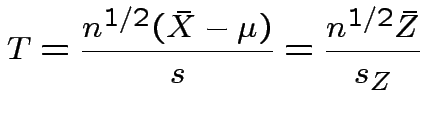
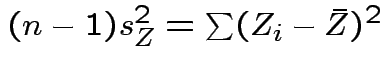 .
.
So: reduced to 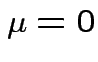 and
and ![]() .
.
Step 1: Define
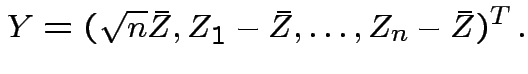
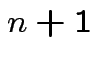 .) Now
.) Now
![$\displaystyle Y =\left[\begin{array}{cccc}
\frac{1}{\sqrt{n}} &
\frac{1}{\sqrt{...
...]
\left[\begin{array}{c}
Z_1 \\
Z_2 \\
\vdots
\\
Z_n
\end{array}\right]
$](img85.gif)
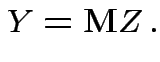
 so we need
to compute
so we need
to compute
 |
![$\displaystyle = \left[\begin{array}{c\vert cccc} 1 & 0 & 0 & \cdots & 0 \\ \hli...
...ots & -\frac{1}{n} \\ 0 & \vdots & \cdots & & 1-\frac{1}{n} \end{array} \right]$](img91.gif) |
|
![$\displaystyle = \left[\begin{array}{c\vert c} 1 & 0 \\ \hline \\ 0 & {\bf Q} \end{array} \right] \,.$](img92.gif) |
Put
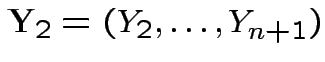 . Since
. Since
 are independent and each is normal.
are independent and each is normal.
Thus
 is independent of
is independent of
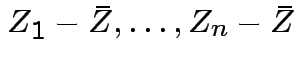 .
.
Since ![]() is a function of
is a function of
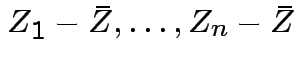 we see that
we see that
 and
and
![]() are independent.
are independent.
Also, see
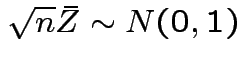 .
.
First 2 parts done.
Consider
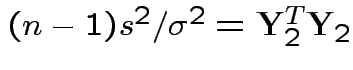 .
Note that
.
Note that
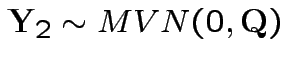 .
.
Now: distribution of quadratic forms:
Suppose
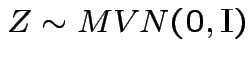 and
and ![]() is symmetric.
Put
is symmetric.
Put
![]() for
for ![]() diagonal,
diagonal, ![]() orthogonal.
orthogonal.
Then
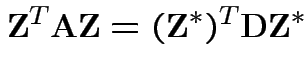
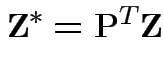
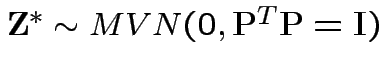 is standard multivariate normal.
is standard multivariate normal.
So:
![]() has same distribution as
has same distribution as
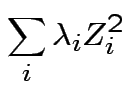
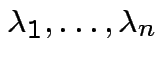 are eigenvalues of
are eigenvalues of
Special case: if all ![]() are either 0 or 1 then
are either 0 or 1 then
![]() has a chi-squared distribution with df
= number of
has a chi-squared distribution with df
= number of ![]() equal to 1.
equal to 1.
When are eigenvalues all 1 or 0?
Answer: if and only if ![]() is idempotent.
is idempotent.
1) If ![]() idempotent and
idempotent and
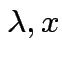 is an eigenpair
the
is an eigenpair
the
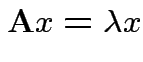
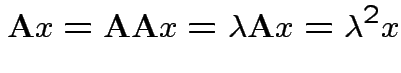
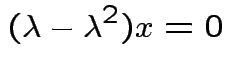
2) Conversely if all eigenvalues of ![]() are 0 or 1 then
are 0 or 1 then
![]() has 1s and 0s on diagonal so
has 1s and 0s on diagonal so
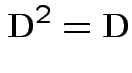

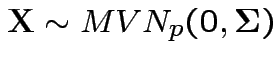 . Then
. Then
Since
![]() it has the law
it has the law
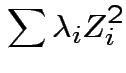
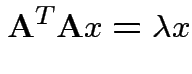
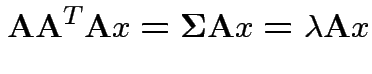
So eigenvalues are those of
![]() and
and
![]() is
is
![]() iff
iff
![]() is idempotent and
is idempotent and
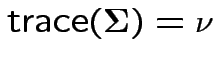 .
.
Our case:
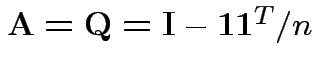 .
Check
.
Check
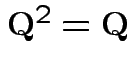 .
How many degrees of freedom:
.
How many degrees of freedom:
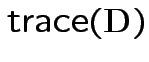 .
.
Defn: The trace of a square matrix ![]() is
is
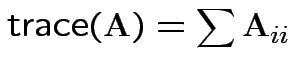
Property:
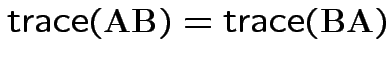 .
.
So:
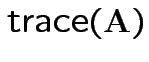 |
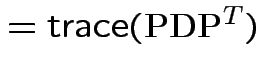 |
|
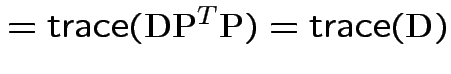 |
Conclusion: df for
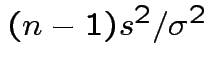 is
is
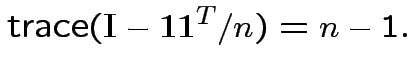
Derivation of the ![]() density:
density:
Suppose
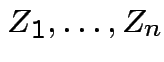 independent
independent 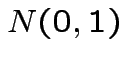 . Define
. Define
![]() distribution to be that of
distribution to be that of
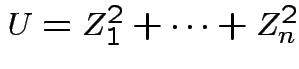 .
Define angles
.
Define angles
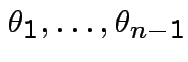 by
by
 |
||
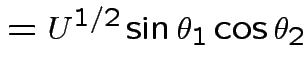 |
||
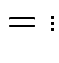 |
||
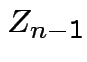 |
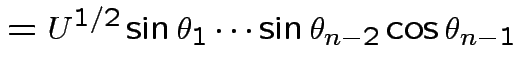 |
|
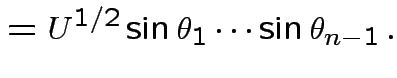 |
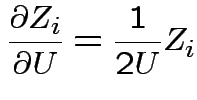
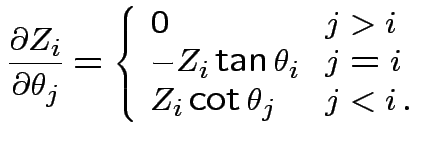
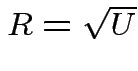 .
.
Matrix of partial derivatives is
![$\displaystyle \left[\begin{array}{ccc}
\frac{\cos\theta_1}{2R}
&
-R \sin\theta_...
...R \cos\theta_1\sin\theta_2
&
R \sin\theta_1\cos\theta_2
\end{array}\right] \,.
$](img162.gif)
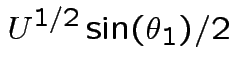
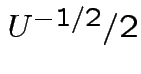 while
every other entry has a factor
while
every other entry has a factor
FACT: multiplying a column in a matrix by ![]() multiplies
the determinant by
multiplies
the determinant by ![]() .
.
SO: Jacobian of transformation is
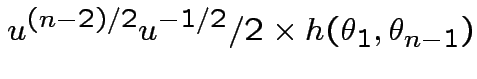
Thus joint density
of
 is
is
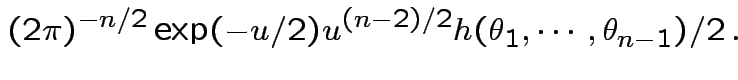
 dimensional
multiple integral
dimensional
multiple integral
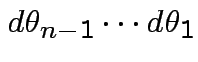 .
.
Answer has the form
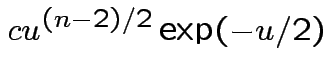
Evaluate ![]() by making
by making
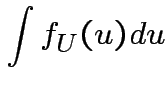 |
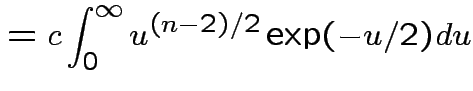 |
|
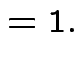 |
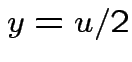 ,
, 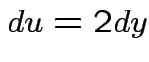 to see that
to see that
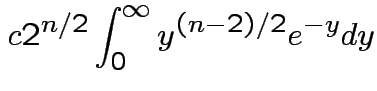 |
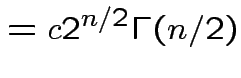 |
|
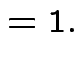 |
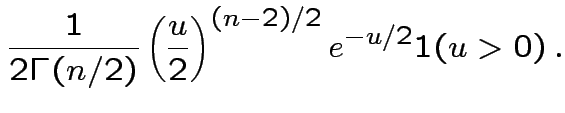
Fourth part: consequence of
first 3 parts and def'n of ![]() distribution.
distribution.
Defn:
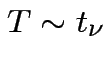 if
if ![]() has same distribution
as
has same distribution
as
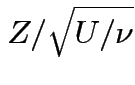
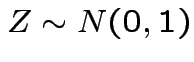 ,
,
 and
and 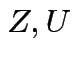 independent.
independent.
Derive density of ![]() in this definition:
in this definition:
 |
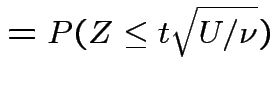 |
|
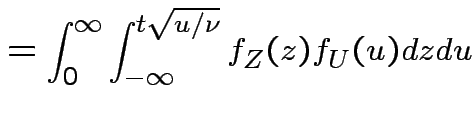 |
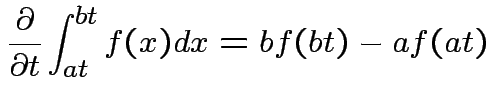
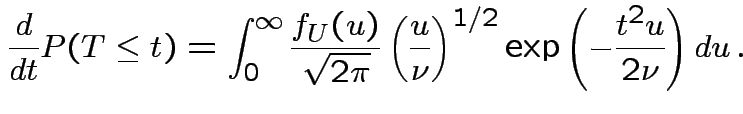
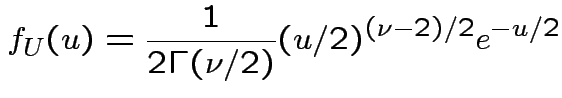

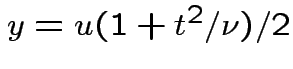 , to get
, to get
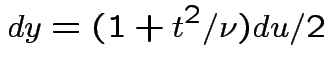
![$\displaystyle (u/2)^{(\nu-1)/2}= [y/(1+t^2/\nu)]^{(\nu-1)/2}$](img200.gif)
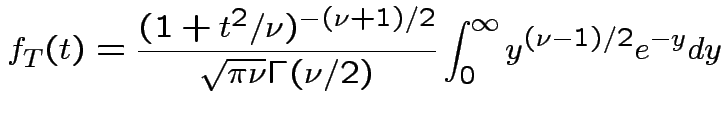

Theorem:
Suppose
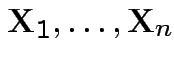 are independent
are independent
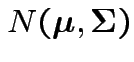 random
variables.
Then
random
variables.
Then
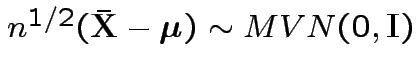 .
.
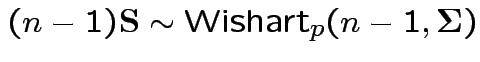 .
.
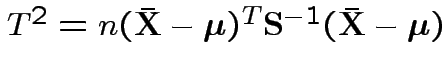 is Hotelling's
is Hotelling's 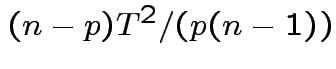 has an
has an 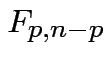 distribution.
distribution.
Proof: Let
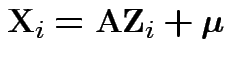 where
where
![]() and
and
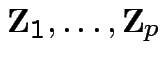 are
independent
are
independent
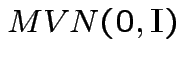 .
.
So
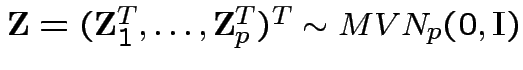 .
.
Note that
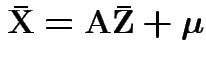 and
and
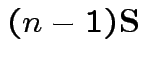 |
 |
|
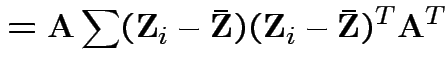 |
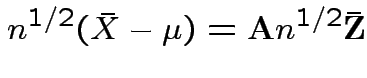
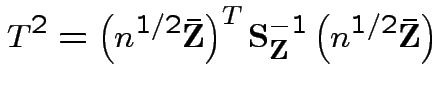
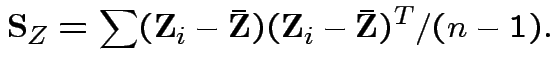
Consequences. In 1, 2 and 4: can assume
 and
and
![]() . In 3 can take
. In 3 can take
 .
Step 1: Do general
.
Step 1: Do general
![]() . Define
. Define
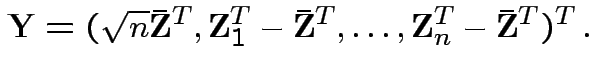
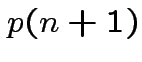 .) Clearly
.) Clearly Compute variance covariance matrix
![$\displaystyle \left[\begin{array}{cc}
{\bf I}_{p\times p} & 0 \\
0 & {\bf Q}^*
\end{array}\right]
$](img228.gif)
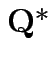 has a pattern. It is a
has a pattern. It is a 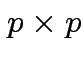 patterned matrix with entry
patterned matrix with entry 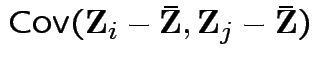 |
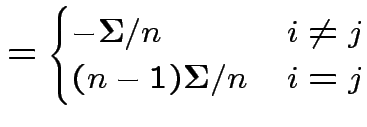 |
|
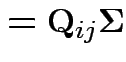 |
Defn: If ![]() is
is
 and
and ![]() is
is
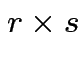 then
then
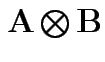 is the
is the
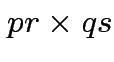 matrix with the pattern
matrix with the pattern
![$\displaystyle \left[\begin{array}{cccc}
{\bf A}_{11}{\bf B}& {\bf A}_{12}{\bf B...
...{\bf B}& {\bf A}_{p2} {\bf B}& \cdots & {\bf A}_{pq}{\bf B}
\end{array}\right]
$](img239.gif)
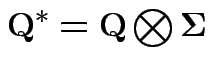
Conclusions so far:
1)
![]() and
and ![]() are independent.
are independent.
2)
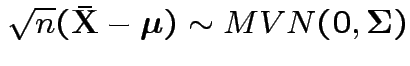
Next: Wishart law.
Defn: The
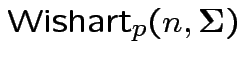 distribution is
the distribution of
distribution is
the distribution of
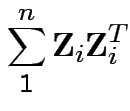
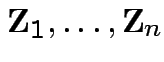 are iid
are iid
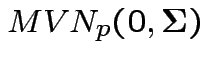 .
.
Properties of Wishart.
1) If
![]() then
then
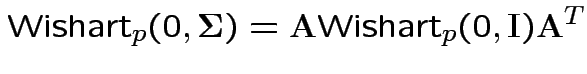
2) if
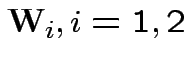 independent
independent
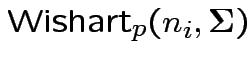 then
then

Proof of part 3: rewrite
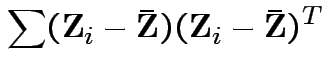
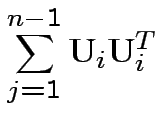
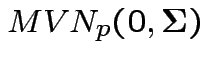 .
Put
.
Put
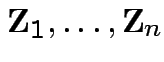 as
cols in matrix
as
cols in matrix 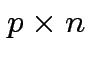 . Then
check that
. Then
check that
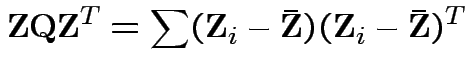
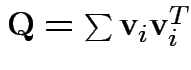 for
for  orthogonal
unit vectors
orthogonal
unit vectors
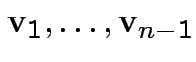 .
Define
.
Define
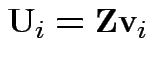
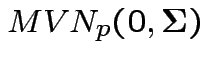 .
Then check that
.
Then check that
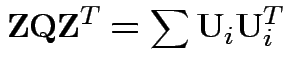
Uses further props of Wishart distribution.
3: If
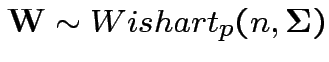 and
and
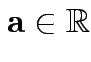 then
then

4: If
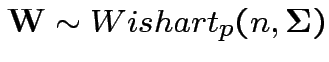 and
and 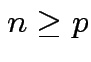 then
then
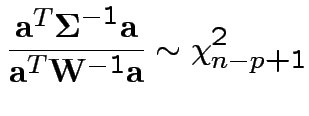
5: If
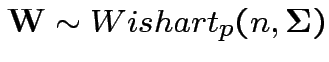 then
then
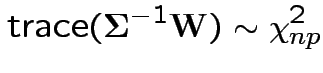
6: If
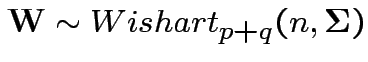 is partitioned
into components then
is partitioned
into components then