STAT 802

Assignment 1

  1. Suppose tex2html_wrap_inline50 has a tex2html_wrap_inline52 distribution with tex2html_wrap_inline54 partitioned as tex2html_wrap_inline56 and Variance covariance

    displaymath58

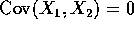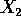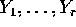    1. Show that tex2html_wrap_inline60 if and only if tex2html_wrap_inline62 and tex2html_wrap_inline64 are independent. Use my definition of MVN; you are not allowed to assume that X has a density. A mathematically careful argument my rely on the fact that if tex2html_wrap_inline68 are independent and 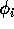tex2html_wrap_inline70 are (measurable) functions then 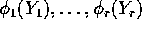tex2html_wrap_inline72 are independent.
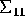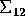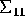    2. Show that whether or not tex2html_wrap_inline74 is singular, each column of tex2html_wrap_inline76 is in the column space of tex2html_wrap_inline74 .
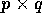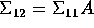    3. Show that there is a matrix A which is tex2html_wrap_inline82 such that tex2html_wrap_inline84 .
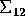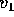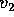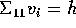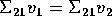    4. Let h be a column of tex2html_wrap_inline76 and tex2html_wrap_inline90 and tex2html_wrap_inline92 be any vectors such that tex2html_wrap_inline94 for i=1,2. Show that tex2html_wrap_inline98 .
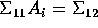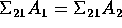    5. Show that if tex2html_wrap_inline100 for i=1,2 then tex2html_wrap_inline104 .
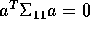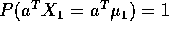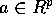    6. Show that tex2html_wrap_inline106 implies tex2html_wrap_inline108 for any tex2html_wrap_inline110 .
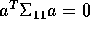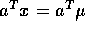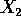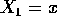    7. Suppose x is such that tex2html_wrap_inline106 implies tex2html_wrap_inline116 . Show that the conditional distribution of tex2html_wrap_inline64 given tex2html_wrap_inline120 is well-defined and is multivariate normal with mean

      displaymath122

      and variance covariance

      displaymath124

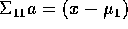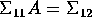      where a is any solution of tex2html_wrap_inline128 and A is any solution of tex2html_wrap_inline132 .

    NOTE: Most facts about tex2html_wrap_inline134 variates X can be demonstrated by writing tex2html_wrap_inline138 for well chosen A.

  2. Fix tex2html_wrap_inline110 . Minimize and maximize tex2html_wrap_inline144 subject to tex2html_wrap_inline146 .
  3. Fix tex2html_wrap_inline110 . Minimize and maximize tex2html_wrap_inline150 subject to tex2html_wrap_inline152 for a given symmetric positive definite matrix Q.
  4. Write out the spectral decomposition of the matrix

    displaymath156

    and then find a symmetric square root.

  5. Suppose tex2html_wrap_inline158 has a MVN distribution with tex2html_wrap_inline160 and

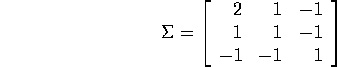
    displaymath162

    Find the conditional distribution of tex2html_wrap_inline62 given tex2html_wrap_inline166 and tex2html_wrap_inline168 . For which values of tex2html_wrap_inline170 and tex2html_wrap_inline172 does this make sense?


Richard Lockhart
Mon Jan 26 10:30:30 PST 1998