STAT 802

Assignment 3

  1. Observations on 2 sexes of two types of wolf (Rocky Mountain and Arctic) are in the file 
    ~lockhart/teaching/courses/802/98_1/assignments/03/q1
    The first 6 are Rocky Mountain males, then 3 females then 10 Arctic males and 6 Arctic females. The 10 variables are 10 different lengths measured on the skulls of the animals (in millimetres).

    1. Use pairwise 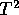tex2html_wrap_inline25 tests to decide if any of the pairs are indistinguishable on the basis of the data here.
    2. Assess whether there are any variables on which all 4 groups have means so similar that the variable in question will not really help discriminate. A hypothesis test with a large tex2html_wrap_inline27 is probably useful.
    3. For the standard linear discriminant rule classify all of the data points and determine the raw and cross-validated error rates.
  2. Fisher's iris data is available in S. Pick a pair of the 4 available variables and plot on a graph the boundaries of the linear and quadratic discriminant rules for discriminating the three varieties of iris along with the data. Estimate misclassification rates parametrically for both discriminant rules but, in estimating the error rates, do not assume that all the variance covariance matrices are the same.

  3. From the text 11.28.

  4. Consider the situation where you have two normal populations and p=1; the populations are tex2html_wrap_inline31 and tex2html_wrap_inline33 . You have samples of size tex2html_wrap_inline35 and tex2html_wrap_inline37 and observe means tex2html_wrap_inline39 and tex2html_wrap_inline41 where we assume that tex2html_wrap_inline43 . We plan to use the following rule:
    R: Classify a new X as coming from population 2 if tex2html_wrap_inline47
    We want to estimate the error rates for this classifier. The usual linear rule for known parameters would classify X in group 2 if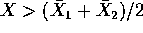 tex2html_wrap_inline51 and have an error rate of

    displaymath53

    where

    displaymath55

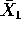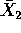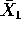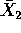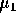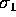    1. Derive an expression for the conditional error rates given tex2html_wrap_inline39 and tex2html_wrap_inline41 of rule R as a function of tex2html_wrap_inline39 , tex2html_wrap_inline41 , tex2html_wrap_inline65 and tex2html_wrap_inline67 .
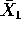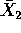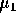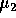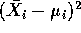    2. Find a Taylor expansion for these quantities as a function of tex2html_wrap_inline39 and tex2html_wrap_inline41 about the points tex2html_wrap_inline65 and tex2html_wrap_inline75 . Keep terms out to quadratic in tex2html_wrap_inline77 .
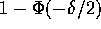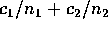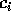    3. Use this expression to compute the expected error rate and show that it is the error rate tex2html_wrap_inline79 for the linear classifier given above plus a term of the form tex2html_wrap_inline81 . Your answer should include a formula for the tex2html_wrap_inline83 .
    4. The cross validation estimate of this error rate is

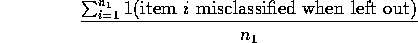
      displaymath85

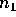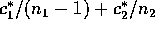      Use the result in the first 3 parts of this question but with tex2html_wrap_inline35 1 smaller get a formula for the expected value of this estimate plus terms like tex2html_wrap_inline89 .

    5. Put these results together to argue that the expected value of the cross validation estimate of the error rates is the same, to terms of order 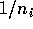tex2html_wrap_inline91 as the expected error rate.

  5. From the text questions 8.17 and 8.18. The data are in

    displaymath93

    and

    displaymath95

  6. From the text questions 9.27 and 9.28.

  7. From the text 10.10.

  8. From the text 12.15.


Richard Lockhart
Tue Mar 3 22:24:25 PST 1998