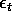be a Gaussian white noise process. Define
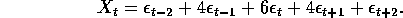
Compute and plot the autocovariance function of X.
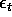are uncorrelated and have
mean 0 with finite variance.
Verify that 
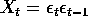is stationary and
that it is wide sense white noise assuming that the 
sequence is
iid.
where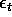 
is an iid mean 0 sequence with variance
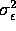. Compute the autocovariance
function and plot the results for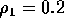 
and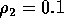 
.
I have shown in class that the roots of a certain polynomial must have modulus more than 1
for there to be a stationary solution X for this difference equation.
Translate the conditions on the roots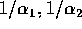 
to get
conditions on the coefficients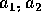 
and plot in the 
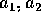plane
the region for which this process can be rewritten as a causal filter
applied to the noise process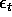 
.
is strictly stationary. If g is some
function from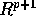 
to R show that
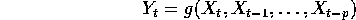
is strictly stationary. What property must g have to guarantee the
analogous result with strictly stationary replaced by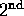 
order
stationary? [Note: I expect a sufficient condition on g; you need not
try to prove the condition is necessary.]
is an iid mean 0 variance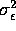 
sequence and that 
are constants.
Define
- Derive the autocovariance of the process X.
- Show that
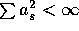implies
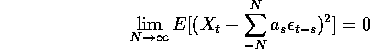
This condition shows that the infinite sum defining X converges ``in the sense of mean square''. It is possible to prove that this means that X can be defined properly. [Note: I don't expect much rigour in this calculation.
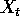with autocorrelation
, 
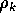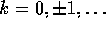and a fixed lag D find the
value of A which minimizes the mean squared error
and for the minimizing A evaluate the mean squared error in terms of
the autocorrelation and the variance of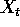 
.
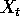is a stationary Gaussian series with mean 
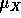and autocovariance 
, 
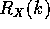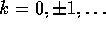. Show that
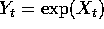is stationary and find its mean and autocovariance.
(Without the 1/2 it's called the variogram.)
Evaluate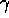 
in terms of the autocovariance of X.