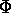 is a Uniform
is a Uniform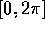 random variable. Define
random variable. Define

Show that X is weakly stationary. (In fact it is strongly stationary so show that if you can.) Compute the autocorrelation function of X.
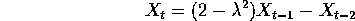
for some value of 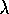 .
Show that the roots of the characteristic
polynomial lie on the boundary of the unit circle in the complex plain. (Hint:
show that
.
Show that the roots of the characteristic
polynomial lie on the boundary of the unit circle in the complex plain. (Hint:
show that 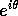 is a root if
is a root if 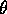 is chosen correctly. Do not spend too
much time on this question; the point is to illustrate that AR(2) models can be found
whose behaviour is much like a sinusoid.)
is chosen correctly. Do not spend too
much time on this question; the point is to illustrate that AR(2) models can be found
whose behaviour is much like a sinusoid.)
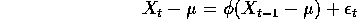
where the 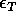 are iid
are iid 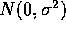 in each of the following ways
in each of the following ways
- By full maximum likelihood. (Maximize the joint density of the X's over the
parameters
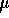 ,
, 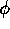 and
and 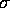 .)
.)
- By estimating
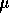 by the sample mean and then doing full maximum likelihood
for the model
by the sample mean and then doing full maximum likelihood
for the model

where
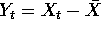 .
.
- By estimating
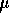 by the sample mean and then doing conditional
maximum likelihood for the previous model.
by the sample mean and then doing conditional
maximum likelihood for the previous model.
Remarks: I do not want you to use ar or other built-in S time-series functions to do these but you may want to use them to get starting values for estimates. It is probably easier to do the methods in reverse order, using the results as starting points for iterative solutions.
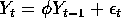 and for the ARIMA(1,1,0) model
and for the ARIMA(1,1,0) model
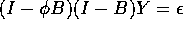 . Compute the limits of the forecast standard
errors for these two models as La tends to infinity.
. Compute the limits of the forecast standard
errors for these two models as La tends to infinity.