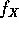STAT 804: 97-3

Assignment 5

1. Suppose X and Y are stationary independent processes with respective spectra and 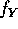. Compute the spectrum of Z=aX+Y.

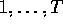2. Suppose X and Y are jointly stationary processes and we observe them at times . Define the sample cross covariance 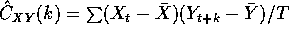where are terms with index larger than T are interpreted as 0. Show that the sample cross covariance can be computed from the discrete Fourier transforms via

   

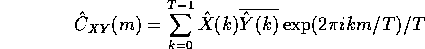
   (or figure out the correct formula).

3. Derive the frequency response function for the recursive filter

   

   and plot the modulus squared and argument of the result for 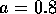and .

4. Compute and plot estimates of the spectrum for the time series fake for varying degrees of smoothing and compare the result to the spectrum of your fitted ARIMA model.

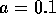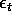5. Let be a Gaussian white noise process. Define

   

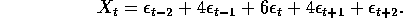
   Compute and plot the spectrum of X.

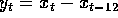6. For the filters A: , B: 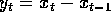and C defined by applying A then B determine the power transfer functions, plot them and interpret their effect on a spectrum. What is the effect of these filters on seasonal series? (Consider what the spectrum of a series with a strong seasonal effect is like.)

DUE: 5 December