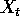STAT 804: 97-3

Assignment 4

Suppose that 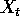is an ARMA(1,1) process

1. Suppose we mistakenly fit an AR(1) model (mean 0) to X using the Yule-Walker estimate

   

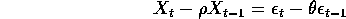
   In terms of , and what is close to?

   Solution: This is a ratio of two sample covariances. Each converges, as to the corresponding theoretical covariance so that . In the previous assignment we computed and found that the lag 1 autocorrelation is

   

   This is the limit of .

2. If we use this AR(1) estimate and calculate residuals using what kind of time series is ? What will plots of the Autocorrelation and Partial Autocorrelation functions of this residual series look like?

   Solution: Let denote the autocovariance at lag 1. For large values of T we may write approximately

   

   or or just

   

   which makes an ARMA(1,2) process. By way of answer about the plots I was merely looking for the knowledge that the plots will match those of an ARMA(1,2) with autoregressive parameter and MA parameters and . The model identification problem may well be somewhat harder. It is a useful exercise to generate some data with ar.sim from an ARIMA(1,0,1) and try to model fitting process. Look at what happens if you fit an AR(1) and then look at the residuals; you don't see anything helpful in general.