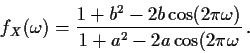Postscript version of these notes
STAT 804
Lecture 22 Notes
Properties of the Periodogram
The discrete Fourier transform
is periodic with period 1 because all the exponentials have period 1.
Moreover,
so that the periodogram satisfies
Thus the periodogram is symmetric around
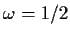 which is called
the Nyquist or folding frequency. (The value is always 1/2
in cycles per point but usually it would be converted to cycles per time
unit like year or day or whatever.)
which is called
the Nyquist or folding frequency. (The value is always 1/2
in cycles per point but usually it would be converted to cycles per time
unit like year or day or whatever.)
Similarly the power spectral density fX given by
is periodic with period 1 and satisfies
which is equivalent to
Spectra of Some Basic Processes
Here I compute the spectra of a few basic processes directly
and then indirectly by a more powerful technique.
Direct from the definition
- White Noise:
- Since
 for all non-zero k we
have
for all non-zero k we
have
- MA(1):
- For
 we have
we have
 and
and
 so that
so that
- AR(1):
- We have
 and
and
Using filters
Any mean 0 ARMA(p,q) process can be rewritten in MA form as
and then the covariance of X is
Although the covariance simplifies for white noise, let us simply write
C(t+h-r -(t-s)) = C(h+s-r) for the covariance in this double sum so that
the calculation will apply to any stationary  .
Then plug this double sum into the definition of fX to get
.
Then plug this double sum into the definition of fX to get
Now write the h in the complex exponential in the form
(h+s-r) +r-sand bring the sum over h to the inside to get
Finally make the substitution k=h+s-r in the inside sum and define
to see that
or
The function A (or 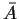 )
is called the frequency response
function and |A|2 the power transfer function. The jargon gain
is sometimes used for |A|.
)
is called the frequency response
function and |A|2 the power transfer function. The jargon gain
is sometimes used for |A|.
The Spectrum of an ARMA(p,q)
An ARMA(p,q) process X satisfies
so that if Y is the process
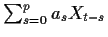 then
then
where
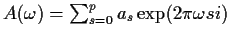 .
At the same time
.
At the same time
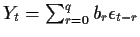 so
so
where
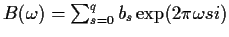 .
Hence
.
Hence
For example, in the ARMA(1,1) case
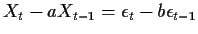 we find (referring to our MA(1) calculation above that
we find (referring to our MA(1) calculation above that
 and
and
 so that
so that



Richard Lockhart
1999-10-13
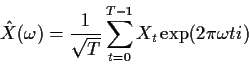
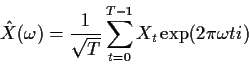
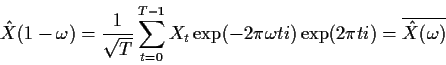
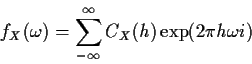


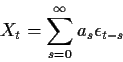

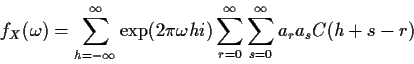
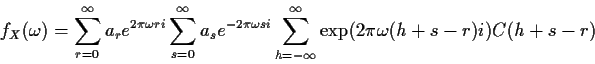
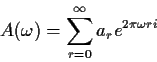
![]() )
is called the frequency response
function and |A|2 the power transfer function. The jargon gain
is sometimes used for |A|.
)
is called the frequency response
function and |A|2 the power transfer function. The jargon gain
is sometimes used for |A|.
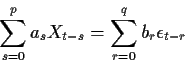
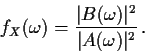
![]() we find (referring to our MA(1) calculation above that
we find (referring to our MA(1) calculation above that
![]() and
and
![]() so that
so that