Introduction



Next: The offspring distribution
Up: Maximum likelihood estimation of
Previous: Maximum likelihood estimation of
The Bienaymé-Galton-Watson (BGW) process was introduced by
Irénée-Jules Bienaymé
(1845) to explain mathematically the observed phenomenon (Malthus,
1817,
de Châteauneuf, 1845) that family names, both among aristocracy
and
among bourgeoisie, tend to become extinct. The process has since
found
uses in many other areas, such as genetics (Ewens, 1969),
epidemiology
(Becker, 1977), queueing theory (Kendall, 1951), and demography
(Keyfitz,
1985). Statistical methods for these branching processes were first
developed by Harris (1948), and have been the target of extensive
research
for the last two decades.
To define the process, let 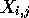 ,
,  be independent, identically distributed random variables, taking
values
in the nonnegative integers, with probability generating function
be independent, identically distributed random variables, taking
values
in the nonnegative integers, with probability generating function
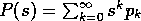 .
We assume throughout that we are in the supercritical case, i.e.,
that
.
We assume throughout that we are in the supercritical case, i.e.,
that
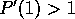 .
The BGW branching process
.
The BGW branching process 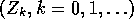 with offspring distribution
with offspring distribution 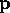 , starting from
, starting from 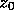 ancestors, is defined recursively by
ancestors, is defined recursively by 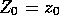 and
and

where  is taken to mean 0. We will assume that
is taken to mean 0. We will assume that 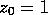 .
It is clear from (1) that
.
It is clear from (1) that 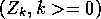 is a Markov chain with
transition probabilities given by
is a Markov chain with
transition probabilities given by
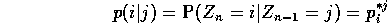
where 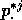 are the probabilities of a
are the probabilities of a 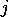 -fold convolution
of
the offspring distribution.
-fold convolution
of
the offspring distribution.
Since, unless 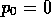 , the process
, the process 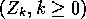 has positive
probability of hitting the
absorbing state 0, it is not possible to estimate any parameters
consistently.
Usually, therefore, inferences are made conditional upon non-
extinction
(Sweeting, 1986, argues the approximate ancillarity of this
conditioning).
Lockhart (1982) showed that two branching processes with the same
mean,
variance, and lattice, and finite
has positive
probability of hitting the
absorbing state 0, it is not possible to estimate any parameters
consistently.
Usually, therefore, inferences are made conditional upon non-
extinction
(Sweeting, 1986, argues the approximate ancillarity of this
conditioning).
Lockhart (1982) showed that two branching processes with the same
mean,
variance, and lattice, and finite 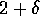 moments cannot be
distinguished, even on the set of non-extinction, on the basis of a
path
of observed generation sizes. In essence, large generation sizes
behave
like normal random variables, since they are the sum of a large
number
of iid random variables.
Dion (1974,1975) exhibited conditionally consistent estimators of
the
offspring mean and the offspring variance. The estimator of the
mean,
namely
moments cannot be
distinguished, even on the set of non-extinction, on the basis of a
path
of observed generation sizes. In essence, large generation sizes
behave
like normal random variables, since they are the sum of a large
number
of iid random variables.
Dion (1974,1975) exhibited conditionally consistent estimators of
the
offspring mean and the offspring variance. The estimator of the
mean,
namely

which Harris derived as the maximum likelihood estimator based on
observing
the entire family tree,
was shown to be a nonparametric maximum likelihood estimator
even when only
observing generation sizes by Feigin (1977) and, independently,
by Keiding and Lauritzen (1978).
In general, there are no (conditionally) consistent
estimates of other interesting parameters such as the extinction
probability
or the offspring distribution.
Dion et al. (1982) discussed maximum likelihood estimation of
the offspring distribution of the BGW-process. They concentrated
on the case where the distribution is supported on three points. The
results of Lockhart show that in this case it may be possible to
consistently estimate the offspring distribution
on the explosion set.
Guttorp (1991) gave an
algorithm for the computation of the offspring distribution mle
which is considerably simpler than the method proposed by
Dion et al. The algorithm is given and the
induced estimate of the offspring variance is described in section 2.
We know that the variance is consistently estimable, and that the
offspring
distribution is not, but we cannot immediately deduce that the mle
of
the variance (based on the inconsistent mle of the offspring
distribution)
is consistent. Guttorp (1991) proved consistency for the case of
distributions
with finite support and having all positive probabilities bounded
below by
some  . The latter condition was needed to allow the
assumption of
fixed lattice size. In this paper we remove this condition.
Section 3 is devoted to a technical tool needed
to establish consistency; namely a local limit theorem for discrete
random variables which does not (as do most such results in the
literature)
assume that the lattice size of the random variables are known and
equal.
In section 4 we apply this result to show consistency, still under
fairly restrictive
regularity conditions, and section 5 consists of some discussion of
possible
extensions.
. The latter condition was needed to allow the
assumption of
fixed lattice size. In this paper we remove this condition.
Section 3 is devoted to a technical tool needed
to establish consistency; namely a local limit theorem for discrete
random variables which does not (as do most such results in the
literature)
assume that the lattice size of the random variables are known and
equal.
In section 4 we apply this result to show consistency, still under
fairly restrictive
regularity conditions, and section 5 consists of some discussion of
possible
extensions.



Next: The offspring distribution
Up: Maximum likelihood estimation of
Previous: Maximum likelihood estimation of
Richard Lockhart
Thu Oct 26 23:26:04 PDT 1995
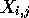 ,
,  be independent, identically distributed random variables, taking
values
in the nonnegative integers, with probability generating function
be independent, identically distributed random variables, taking
values
in the nonnegative integers, with probability generating function
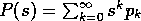 .
We assume throughout that we are in the supercritical case, i.e.,
that
.
We assume throughout that we are in the supercritical case, i.e.,
that
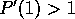 .
The BGW branching process
.
The BGW branching process 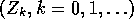 with offspring distribution
with offspring distribution 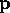 , starting from
, starting from 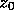 ancestors, is defined recursively by
ancestors, is defined recursively by 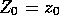 and
and
 is taken to mean 0. We will assume that
is taken to mean 0. We will assume that 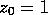 .
It is clear from (1) that
.
It is clear from (1) that 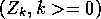 is a Markov chain with
transition probabilities given by
is a Markov chain with
transition probabilities given by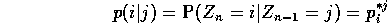
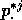 are the probabilities of a
are the probabilities of a 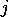 -fold convolution
of
the offspring distribution.
-fold convolution
of
the offspring distribution.
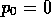 , the process
, the process 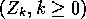 has positive
probability of hitting the
absorbing state 0, it is not possible to estimate any parameters
consistently.
Usually, therefore, inferences are made conditional upon non-
extinction
(Sweeting, 1986, argues the approximate ancillarity of this
conditioning).
Lockhart (1982) showed that two branching processes with the same
mean,
variance, and lattice, and finite
has positive
probability of hitting the
absorbing state 0, it is not possible to estimate any parameters
consistently.
Usually, therefore, inferences are made conditional upon non-
extinction
(Sweeting, 1986, argues the approximate ancillarity of this
conditioning).
Lockhart (1982) showed that two branching processes with the same
mean,
variance, and lattice, and finite 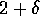 moments cannot be
distinguished, even on the set of non-extinction, on the basis of a
path
of observed generation sizes. In essence, large generation sizes
behave
like normal random variables, since they are the sum of a large
number
of iid random variables.
Dion (1974,1975) exhibited conditionally consistent estimators of
the
offspring mean and the offspring variance. The estimator of the
mean,
namely
moments cannot be
distinguished, even on the set of non-extinction, on the basis of a
path
of observed generation sizes. In essence, large generation sizes
behave
like normal random variables, since they are the sum of a large
number
of iid random variables.
Dion (1974,1975) exhibited conditionally consistent estimators of
the
offspring mean and the offspring variance. The estimator of the
mean,
namely
 . The latter condition was needed to allow the
assumption of
fixed lattice size. In this paper we remove this condition.
Section 3 is devoted to a technical tool needed
to establish consistency; namely a local limit theorem for discrete
random variables which does not (as do most such results in the
literature)
assume that the lattice size of the random variables are known and
equal.
In section 4 we apply this result to show consistency, still under
fairly restrictive
regularity conditions, and section 5 consists of some discussion of
possible
extensions.
. The latter condition was needed to allow the
assumption of
fixed lattice size. In this paper we remove this condition.
Section 3 is devoted to a technical tool needed
to establish consistency; namely a local limit theorem for discrete
random variables which does not (as do most such results in the
literature)
assume that the lattice size of the random variables are known and
equal.
In section 4 we apply this result to show consistency, still under
fairly restrictive
regularity conditions, and section 5 consists of some discussion of
possible
extensions.