Optics Experiment 1
Reflection,
Refraction and POLARIZATION OF LIGHT
References
Objectives
I. Observe straight-line propagation of light
II. Study the law of reflection
III Study the law of refraction (Snell*s Law)
IV Observe total internal reflection and dispersion
V Produce and detect linearly polarized light
VI Measure Brewster*s angle
Apparatus
|
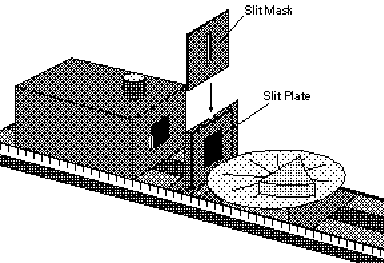
Fig. 1.1: Basic Ray Optics Setup |
From the Optics Kit: Optics Bench, Light Source, Ray Table and Base Component Holders (2), Slit Plate, Slit Mask, Viewing Screen, Ray Optics Mirror, cylindrical lens, Polarization Filters.
Introduction
Many useful properties of light can be understood with a simple ray theory (geometric optics). When light travels through air of uniform density, it propagates in a straight line from its source. One can use a slit plate to select ※rays§ of light coming from a point source.
If light encounters a shiny surface it undergoes specular reflection. Rays reflect from mirrors according to the law of reflection: the angle of incidence equals the angle of reflection where the angle is measured from the normal to the reflecting surface.
When light travels from a medium to another, such as from air to water, it changes the direction of propagation. This phenomenon is called refraction. If the angle of incidence is not normal (at right angles) to the boundary then the direction changes according to Snell's law:
n1 sin
q1 = n2 sin q2
(1)
where n1 and n2 are constants called indices of refraction of the two media. The angles q1 and q2 are the angles the light ray makes with the normal to the boundary between the two media.
In
this experiment, we will also study the polarization of light, a property that
can be explained by the wave theory. We will focus on linear polarization of
light and leave circular polarization for future studies.
Procedure
Part I - Preliminary Observations on Straight-Line Propagation
Set the equipment as shown in Fig 1.1. You may leave off the viewing screen at first. Plug in the light source and turn it on. The bulb has a linear filament running up and down.
1. Does light travel in a straight line from its source? Observe the rays that emerge from the slit plate. Look at the rays on the ray table then lower your head and peer along a ray. Are you sure that the rays do not bend as they pass through the slits?
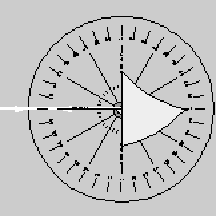
|
Fig. 1.2: Single Ray Setup |
2. Find how to get sharp rays. Vary the distance between the slit plate and the light source and note how the width, brightness and sharpness of the rays change. Observe how the distinctness and the direction of the rays change as you rotate the slit plate so that the slits are not parallel with the light bulb*s filament.
Summarize your findings of steps 1 and 2 using only a few sentences
Part II - The Law of Reflection
Set
up the equipment as shown in Figure 1.2. Adjust the components so that a single
ray of light is aligned with the bold arrow labelled
※
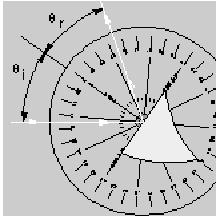
1. Measure angles of incidence and reflection. Choose about six different angles ranging from 0∼ through 90∼. Rotate the ray table to each of these incidence angles (qi) and measure the corresponding angle of reflection (qr1). Repeat your measurements with the incident ray coming from the opposite side of the normal (qr2). Make sure you tabulate these data directly in your lab notebook.
2. Analyze your data and determine the law of reflection. Are the results from the two trials the same? If not why not?
Part of the law of reflection states that the incident ray, the reflected ray and the normal to the reflecting surface lie in the same plane. Is this adequately tested by this experiment?
|
Fig. 1.3: Alignment
of the Ray Mirror for normal incidence and for incidence at an arbitrary
angle |
Part III - The Law of
Refraction: Snell*s Law (E)
1. Align a ray along the table's optical axis.
Mount the light source on the optical bench. Place the slit plate and slit
mask on opposite sides of a component holder so that the centring
notch points to the slit that is not covered by the slit mask. Put the ray
table on its base, degree side up, and align all the components against the
alignment rail as in Fig. 1.4. Turn on the light source and turn the filament
knob and adjust the slit plate until one single ray coincides with the
2. Measure angles of incidence and refraction. Place the cylindrical lens on the COMPONENT line of the ray table so that the ray hits the flat side of the lens. Choose several angles ranging from 0∼ to 90∼ and measure the angle of refraction for each angle of incidence chosen. You can make two measurements for each angle: one clockwise from the normal, the other counterclockwise. This will compensate for slight misalignment of the lens on the table. Plot your points roughly as your take the data.
3. Check the reversibility of Snell's Law. Put the cylindrical lens on the other side of the COMPONENT line so that the ray hits the curved side. Measure some of the same angles you used in the last section to check the reversibility of Snell*s law. What do you conclude?
|
|
Graph your results. Is your graph linear? Do the data from parts 2 and 3 agree? If your answer is no, try to modify your graphing methods so that all the data follow a linear relationship. What does the slope mean? What does the intercept mean?
IV - Dispersion and Total
Internal Reflection
The index of refraction in most media depends on the wavelength. For the acrylic lens, this means that different colours emerge from the lens at different angles. This effect, known as dispersion, is most obvious for large angles of refraction near 90∼.
1. Observe dispersion. Leave the Parallel Ray Lens in place and insert the Slit Mask over the Slit Plate so that only one central ray is transmitted. Rotate the table so that the ray emerges from the Cylindrical Lens near 90∼. You should be able to see the ray split into a rainbow of colours from blue to red on the table. You can mount the viewing screen on the Ray Table Component Holder and place this on the table to view and measure the angular dispersion of the colours. Measure the angles of the two extremes of the visible spectrum you see: blue and red. Estimate their respective refractive indices.
When light rays hit the surface between media of different refractive indices, there is always a reflected ray. There may or may not be a refracted ray going into the other medium. When the index of refraction of the medium from whence the light ray comes is larger than the index on the other side then there is an angle of incidence above which no ray is transmitted through the surface. The critical angle is the angle of incidence for which the refracted ray*s angle is exactly 90∼. Light incident above the critical angle is totally reflected. This is called total internal reflection.
2. Measure the critical angle. Leave the Parallel Ray Lens and Slit Mask in place. With the Cylindrical Lens on the Ray Table, rotate the table until the critical angle is reached. Measure this angle. You may wish to use one of the coloured filters because the critical angle will depend on which colour you look at.
V 每 Production and Detection of Linearly Polarized Light
In the wave theory, to describe light one must specify its frequency, its direction of propagation and its state of polarization. Our interest in this part of the lab is with polarization, so let us assume that we have monochromatic light propagating along the +direction of a right-handed coordinate system. Light is a transverse electromagnetic wave〞the electric field is always perpendicular to the direction of propagation. Because the direction of propagation is along the +axis, the electric field vector E must lie in the plane formed by the x and y axes. This can be expressed mathematically as follows:
E( x,y,z,t) = Ex (z,t) + Ey (z,t) (2)
The components of the electric field Ex and Ey do not depend on x and y because we assume that the wave is a plane wave propagating along the +direction.
Light is linearly polarized if the electric field vector E is always parallel to the same line which is perpendicular to the direction of propagation. Mathematically
E(z,t) = Ax cos(wt 每 kz) + Ay cos(wt 每 kz) (3)
|
|
The amplitudes Ax and Ay are real constants. The intensity of the light is proportional to the square of the amplitude. Fig.1.5 shows the electric field vectors at a fixed time along a line in the direction of propagation. Fig1.5(a) illustrates light polarized along the direction (Ax≧0, Ay=0) and (b) shows polarization along the +direction (Ax=0, Ay≧0). As time goes on the entire pattern moves in the +direction. Light polarized in an arbitrary plane is a superposition of these two independent possibilities (Ax≧0, Ay≧0). The plane of polarization is determined by the relative magnitudes of Ax and Ay.
Note: Light can be circularly or elliptically polarized if the there is a phase difference between the x- and y- components of the electric field (the tip of the electric field vector moves in a circle or ellipse). We do not study circularly or elliptically polarized light in this lab.
Most light sources do not produce polarized light. Individual atoms in the source radiate independently. Although at any instant in time light received from a radiating atom in the source has a definite state of polarization, the state of polarization changes rapidly with time. You may think of unpolarized light as having two polarization components which are radiated independently and randomly. Between polarized light which has a fixed relation in time between the amplitude and phase of the two polarization components and unpolarized light which has a random relation in time between the two polarization components, is partially polarized light. Partially polarized light is a mixture of polarized and unpolarized light.
A linear polarizer produces polarized light by selectively absorbing light polarized perpendicular to the polarization axis and transmitting light parallel to the transmission axis. Our HN22 linear polarizers absorb more than 99.99% of the perpendicular component and transmit 44% of the parallel component. Thus the linear polarizer transmits 22% of incident unpolarized light. A perfect polarizer would transmit 50% of incident unpolarized light.
Consider unpolarized light falling on a polarizer which only transmits the components parallel to the axis. The filtered light has amplitude A and intensity I = A2. Let this filtered light fall on a second polarizer whose polarization axis ¢ is at an angle q with respect to the axis. The incident light has components A cos q and 每A sin q along the ¢ and ¢ axes. If both polarizers are perfect, the intensity after the second polarizer would be |A cos q|2 but for the nonideal polarizers the transmitted intensity is 0.44 |A cos q|2.
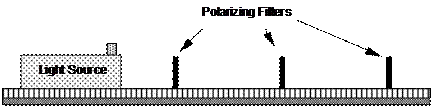
For the following experiments, mount the light source and filters on the optical bench as shown in Fig. 1.6.
A. Verify that light from the light source is unpolarized
Look at the light source through a linear polarizer while rotating the polarizer through 360∼. If the light source is unpolarized, no variation in intensity will be observed.
B. Verify that a linear polarizer can be used as a linear analyzer
Produce linearly polarized light with a linear polarizer. Look at this light through a second linear polarizer, the analyzer. When the analyzer is rotated through 360∼ alternate maxima and minima are seen every 90∼. If the axis of the first polarizer is set at an angle q, then maxima are seen when the analyzer is set at q and q+180∼, and minima are seen when the analyzer is set at q+90∼ and q+270∼.
C. Understand the following nonintuitive experiment
Mount two linear polarizers some distance apart with their polarization axes oriented at 90∼ with respect to each other. Observe that no light is transmitted through the pair. Mount a third linear polarizer between them. Upon rotation of the middle polarizer through 360∼ maximum and minimum transmission is observed alternately every 45∼.
|
|
Part VI - Brewster*s Angle
When unpolarized light reflects from a nonmetallic surface, it is at least partially polarized after reflection. Reflect a ray off the flat surface of the Cylindrical Lens and observe the reflected ray through a linear analyzer. (You may look directly at the reflected light or project it onto a screen.) Do you observe any polarization dependence of the reflected ray? Do the same observation on the refracted ray emerging from the curved surface of the Cylindrical Lens.
Now polarize the incident ray by setting the linear polarizer at 90∼ and placing it between the light source and the Cylindrical Lens. Project the reflected ray onto a screen. Rotate the Ray Table and Cylindrical Lens and observe the intensity of the reflected ray as a function of angle. If you see a minimum or maximum in the reflected intensity of the polarized ray, note the angle at which this occurs. Also record the angles of the reflected and refracted rays at this position and calculate the angle between them. Set the polarizing filter at 0∼ and try the same experiment.
Try the same experiments with the Ray Optics Mirror.
|
Fig.
1.7: Setup to observe
polarization of reflected light and to measure Brewster*s angle |
Prelab questions
- When you measure the law of reflection and the law of refraction, you are supposed to make two measurements for each angle: one clockwise from the normal, the other counterclockwise. What is the advantage of doing that?
- Explain the concept of critical angle. Why does it depend on the colour of light?
- What is Brewster*s angle? Draw a diagram to explain how to measure Brewster*s angle using the optics kit available in the lab.
- Explain why it may help to wear polarizing glasses when go fishing.