Weekly commentary: MAT335 - Chaos, Fractals and Dynamics

March 21

A two dimensional discrete dynamical system is defined by a function H(x,y) of two variables (x,y). The orbits of H are the sequences {(x_0,y_0), H(x_0,y_0), H^2(x_0,y_0), ... } . Here, (x_0,y_0) is the initial point of the orbit, which is obtained by iterating the function H just as we did for one dimensional discrete systems like the logistic function. In the two dimensional case it is convenient and informative to plot the orbits on the x,y-plane. Fixed points and periodic points are defined the same as in the one dimensional case: p is a fixed point of H if H(p) = p, and q is a periodic point of H of period k if H^k(q) = q (Here I am writing p and q as two dimensional vectors, and as usual H^k denotes the k-fold convolution of H with itself, not the product).

The simplest two dimensional systems are the linear and affine ones. A linear dynamical system is one of the form H(z) = Az where A is a 2 by 2 matrix (and z denotes a two dimensional vector). An affine system is one of the form H(z) = Az + v, where v is some vector. 0 is always a fixed point of a linear system (but not of an affine system). Here are some examples of linear systems.

• A is diagonal with entries a,a. If 0
• A is rotation about the origin. Here all orbits lie on circles centred about (0,0).
• H(z) = v. Here all orbits move along straight lines parallel to the vector v and passing through the initial point of the orbit (this kind of transformation is called a "translation").

An invariant set for H is a subset B of the x,y-plane that has the property; H(B) is contained in B. In other words, if z is in B, then H(z) is in B too, and so the entire orbit of z is in B. Some examples of invariants sets; any fixed point and any orbit are invariant sets. If H(z) = Az where A is a rotation, then any circle centred at the origin is an invariant set. If H(z) = v (translation), then any line parallel to v is an invariant set for H.

For any invariant set B of H, we define the basin of attraction of B to be the set W(B) = { z such that H^n(z) approaches B as n tends to infinity}. W(B) is also called the stable set of B. Going back to the examples above, if H(z) = Az where A is diagonal with entries a,a, in the case 0< a <1, W(0,0) is the whole x,y-plane, while in the case 1 < a, W(0,0) is just (0,0).

To describe the dynamics of a two dimensional dynamical system (or a dynamical system of any dimension for that matter), one looks for the invariant sets and their stable sets (or at least tries to!). This information goes a long way towards a complete description of the dynamics (i.e., of the behavior of the orbits).

The Henon map is a two dimensional discrete dynamical system proposed by M. Henon in 1976 as a model for chaotic behavior in two dimensions. Here the function H(x,y) is nonlinear (linear systems are quite easily understandable). The function is defined by H(x,y) = (y+1-ax^2, bx). Here, a and b are parameters; adjusting them will change the dynamics (orbits) of H (we will usually be interested in the case a = 1.4 and b = 0.3). 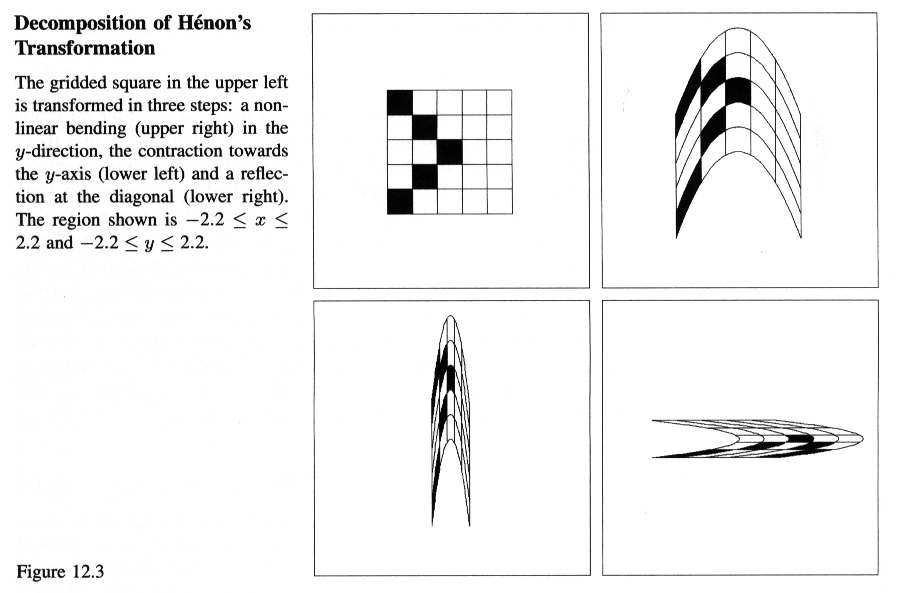( Larger view . This image from Chaos and Fractals, New Frontiers of Science by H.-O. Peitgen, H. Jurgens, and D. Saupe. Springer-Verlag 1992.) To get an idea of what H does to points, it is worth noting that H is can be written as a composition of 3 transformations; a bending, a compression in the x-direction, and a reflection through the diagonal y = x (see page 662). It is this 'stretch-and-fold' action of H (for certain parameter values) that makes this map chaotic (as we'll discuss below).

As is usual in the study of a dynamical system we begin by looking for periodic orbits (including the fixed points). Fixed points and periodic points of H are points (x,y) that solve the equations H^k(z) = z for some k (note that this denotes k-fold composition of H, not the product). We find that for a < (b-1)/4, there are no fixed points. If a = (b-1)/4 there is one fixed point (2/(b-1), 2b/(b-1), and if (b-1)/4 < a there are two fixed points p_1 and p_2. As the parameter a is increased a sequence of period doubling bifurcations occur. Here too we see Universality: the rate at which the bifurcations occur is given by the Feigenbaum constant 4.669... . The period doubling "cascade" is completed when a reaches the value 1.05 (see Figure 12.15).

As in the case of the logistic equation, the period doubling signals the onset of chaos. For parameter values a > 1.05 and b = 0.3, the Henon map possesses an invariant set A situated near the origin. 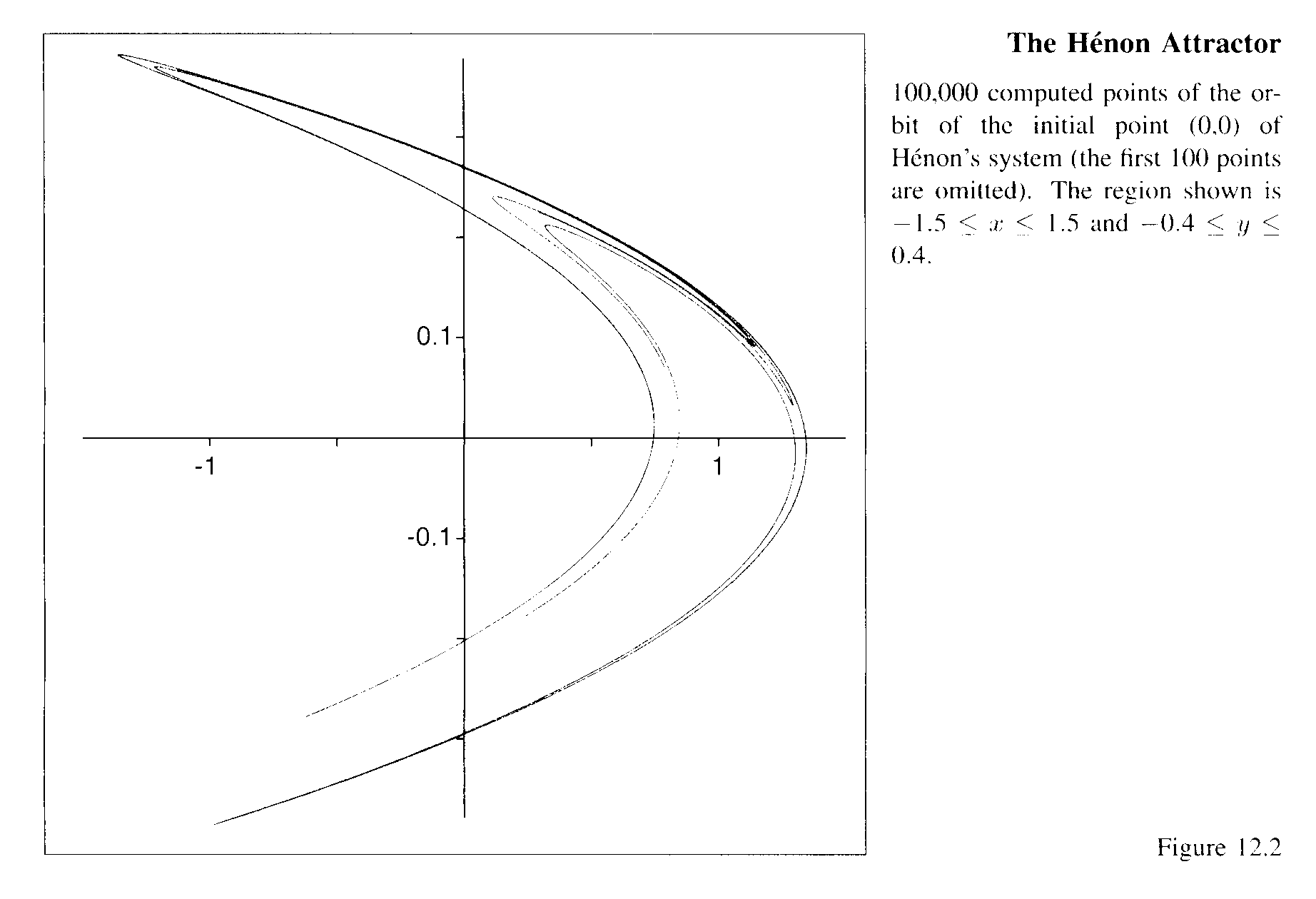( Larger view.) The dynamics on this attractor A is chaotic. That is, points move around the attractor in an apparently random fashion. More precisely, the dynamics of the Henon map on the attractor exhibits the hall marks of chaos: sensitive dependence on initial data, periodic points are everywhere, and there are ergodic orbits (i.e., orbits that visit every neighborhood of the attractor). However, we still lack a mathematical proof that the dynamics on the attractor is chaotic. (See the Henon applet to see the dynamics on the attractor.)

Another feature of the Henon attractor is that it has a fractal-like structure. From afar it looks like a long winding curve, but when you zoom in on a small piece the curve breaks into several thinner strands close together. 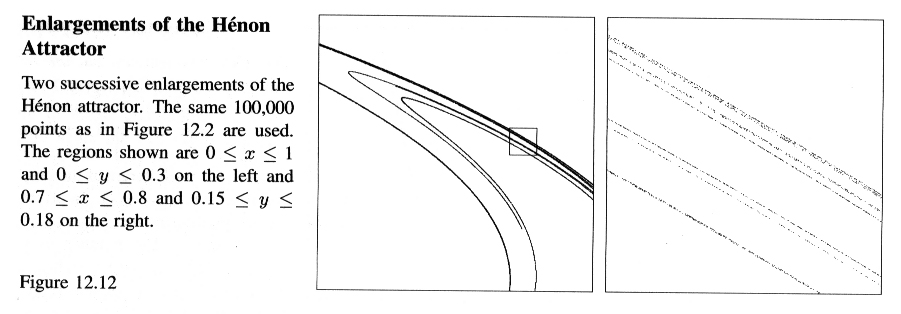( Larger view.) And when you zoom in to one of these smaller strands it too breaks apart into several thinner strands, etc; see Figure 12.12. In fact, one can measure the fractal dimension of the attractor (via the box counting method); it is approximately 1.3 (see page 670). It is this fractal-like structure of the attractor which makes it "strange". If you looked at the attractor for other parameter values (for some parameter values there is no attractor though), it may appear either as a finite set of points (eg., an unstable periodic orbit) or as a solid region (eg., the stable set of a stable periodic orbit) - these attractors are not "strange", and the dynamics on them is not chaotic.

It is the "strangeness" of the strange attractor which makes the dynamics of the Henon map chaotic. Recall that starting with an arbitrary point in the plane, the orbit of that point under iteration by the Henon map will either move outwards to infinity or else will move towards the attractor. In the former case the dynamics is simple (the orbit goes to infinity). In the latter case the orbit becomes quite complicated as it converges to the attractor. When it is very close to the attractor (which doesn't take too long; convergence of orbits to the attractor is exponentially fast, i.e., the distance between points in the orbit and the attractor diminishes like c*e^n for some c > 0 and n < 0), the orbit moves very much like an orbit on the attractor. So there are two types of behavior of this system; one is very regular and the other is chaotic. If it is to model some physical phenomena, then the orbits that go off to infinity are not relevant and what we discover then is that a relatively simple model produces an extremely complicated dynamics. In the years prior to the creation of the "strange attractor" paradigm, if a scientist observed chaotic behavior in his model or experiment he would most likely ascribe it to an incorrect mathematical model of the phenomena or else to errors in the experiment (see David Ruelle's book for his comments about this). Now it is accepted that simple models can be intrinsically complicated to an infinite degree and part of the "boom" in chaos theory were the countless discoveries of chaos in many standard mathematical models that hitherto had not been suspected of producing anything "unpredictable" or "uncontrollable".

Later sections of Chapter 12 describe some of the quantitative measurements one can make of chaotic dynamics such as the Lyapunov exponents (Section 12.5) and reconstruction of strange attractors from experimental data (Section 12.7).