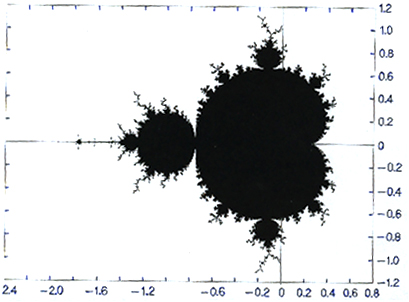
This is the Mandelbrot set. For a closer look, go here . We see that it does not stretch out to infinity. In fact, we can prove that the Mandelbrot set is contained in the circle (in the complex plane) of radius 2 centred at 0;
Here we will consider only the quadratic function q_c(z) = z^2 + c. Let's begin with some general remarks about the dynamics of q_c(z) ( i.e., the behavior of orbits of q_c). To motivate our remarks, we state one of the main theorems of Fatou and Julia : The Julia sets of the quadratic function are either connected (i.e., one piece) or totally disconnected (i.e., dust). Note that whether the Julia set is connected or not is the same as whether the prisoner set is connected or not (since the Julia set is the boundary of the prisoner set). With this in mind we proceed with the following remarks.
Since the Julia sets of the quadratic functions q_c(z) = z^2 + c are either connected or else are dust, it is interesting to classify those complex numbers c such that the Julia set of q_c is connected. This is exactly what Mandelbrot did in 1979. The resulting set has come to be known as the Mandelbrot set. Let M be the Mandelbrot set. Then we have the following definition;

This is the Mandelbrot set. For a closer look, go
here
. We see that it does not
stretch out to infinity. In fact, we can prove that the Mandelbrot set
is contained in the circle (in the complex plane) of radius 2 centred at 0;
M is contained in the set { complex numbers z such that |z| is < or = to 2 }
To prove this we go back to our study of the Julia set of q_c. There we proved that if |z| is greater than the maximum of |c| or 2, then z is in the escape set of q_c (see last week's comments, or look at page 794). Now, we are interested here in whether the Julia set is connected or not (whether c is in M or not) and we are using the second definition above of the Mandelbrot set, so we are interested in whether 0 is in the escape set or not. Note that studying the orbit of 0 is the same as studying the orbit of c, and the orbit of c is in the escape set if |c| is greater than 2 (this is the statement given in the second line of this paragraph). Thus, if |c| is greater than 2 then 0 is in the escape set of q_c and hence the Julia set J_c is disconnected, and so c is not in the Mandelbrot set. Note that there are still many numbers c such that |c| < 2 but the Julia set J_c is disconnected (that is, there are many numbers c, |c| < 2, whose orbit under iteration by q_c tends to infinity).We can understand more of the basic features of the Mandelbrot set by answering the question of whether q_c has a stable periodic orbit or not. Recall the observation mentioned at the top; if q_c has a stable periodic orbit (of any period) then the Julia set J_c must be connected. Hence, if q_c has a stable periodic orbit then c is in M. So let's figure out for which c's the quadratic function q_c(z) has a stable periodic orbit. We noted above that q_c(z) has periodic points of any period, so it is just the matter of figuring out whether any of those periodic points are stable. To do this we use the derivative criteria;
We now proceed with the determination of those c's such that q_c has a stable period 2 point. Here the two equations to solve are (1) (q_c)^2(z) = z and (2) |((q_c_)^2) '(z)| < 1. Following the same procedure as for the fixed points and as described on pages 864 and 865, we find that if c is inside the disc of raduis 1/4 centred at -1 in the complex plane, then q_c has a stable period 2 point and so these c's are in the Mandelbrot set. This disc is the next largest feature of the Mandelbrot set after the main heart-like shaped body (note that it is tangent to the main body at the point -3/4).
Continuing in this fashion we can detemine those c's for which q_c has a
stable period 3 point, a stable period 4 point, etc. Each one of these
sets is a small disc that sits on the edge of the main body and the
size of the disc decreases the larger the period.
 Together these discs and the main body give the gross features of the
Mandelbrot set
(for a closer look, go
here).
Together these discs and the main body give the gross features of the
Mandelbrot set
(for a closer look, go
here).
From the pictures of the Mandelbrot set we can see also that it is symmetric with respect to the real axis (the x-axis if we write complex numbers as x + iy). We can prove this as follows. Suppose c is in the Mandelbrot set. Then S = {0, c, c^2 + c, ...} = the orbit of 0 under q_c, is a sequence of complex numbers that is bounded (re the definition of M given above). Let (c) denote the complex conjugate of c (so if c = x + iy, then (c) = x - iy). Now consider the sequence S ' = {0, (c), (c)^2 + (c), ...} which is the orbit of 0 under q_(c). Note that if S is a bounded sequence then so is S ' and visa versa (do you see why?). Therefore, if c is in the Mandelbrot set then so must be (c). That is, M is symmetric with respect to the x-axis ('M is invariant under complex conjugation').
There is much more to the Mandelbrot set than just the main heart-like body and it's (infinitely) many 'buds' (look again at Figure 14.27). We see complicated 'filaments' projecting outwards from the main body and buds. What c values are these? Well, they are not due to those c's where q_c has a stable periodic orbit because we found all of those already. So they must be due to those c's where q_c has no stable periodic orbits, but the Julia set J_c is still connected. Now the situation is more delicate. For c's that belong to those filaments, the derivative of (q_c)^k(z) at a point z that is a periodic point of period k, has modulus greater than or equal to 1 : |((q_c)^k) ' (z)| > 1 or is = to 1. So the periodic points of q_c for such c's must be either repelling or neutral, respectively. Examples of the former is the line J_c for c = -2 and the 'dendrite' J_c for c = i (see Figure 14.23). An example of the latter is c = -(3/4) (see Figures 14.21 and 14.22).
One finds a remarkable similarity between portions of the Mandelbrot set and certain Julia sets. If one zooms in to a portion of the Mandelbrot set and compares the image to an appropriately magnified portion of a Julia set J_c where the parameter c is chosen from the portion of the Mandelbrot set that was magnified, the images can be essentially identical. This is illustrated in Figures 14.29 and 14.30, and Figure 14.31. In an even more general sense we can talk about the similarity of the Julia sets and the Mandelbrot set. That is, under more general transformations than just magnifications, one can compare portions of the Mandelbrot set with certain Julia sets; this is described in pages 882-895.
I would recommend watching the video, "Fractals: An Animated Discussion" (available at the Audio-Visual Library in Gerstein, call number 002948), to see the remarkable beauty of Julia sets and the Mandelbrot set. Here they have used powerful computer graphics to make 'movies' of Julia sets as the parameter c is changed, as well as illustrating the various forms of Julia sets as the parameter c moves around the Mandelbrot set, and the similarity between the Julia sets and the Mandelbrot set. (The portion containing Julia sets and the Mandelbrot set begins near the middle of the video).