Fractal Landscapes; Variations
These images show the effect of changing the scaling parameter. At each stage in the
construction, a random displacement of the midpoints is made according to the
formula avg + scale*rand where avg is the average of the adjacent
corners, rand is a random number (for these examples, normally distributed
about zero with a variance of 1), and scale is a scaling parameter which
is proportional to 2d*level where level is k, k-1, k-2, ..., 1
for the first iteration, the second iteration, the third iteration,..., the kth iteration. So
the amount of random displacement decreases by a factor of 2d when going
to the next iteration (random displacements become smaller as the construction proceeds to
smaller and smaller scales). So we expect those landscapes that are made with larger d
to have larger extreme variations (due to the first iteration) but relatively smoother surfaces
than landscapes made with smaller d (which will have smaller extreme variations
but rougher surfaces). You can see that in the examples below. (Imagine walking on these
surfaces; for large d you will be going up and down to great heights and depths, but the
surfaces of the 'mountains' will be relatively smooth. While for the smaller d surfaces
you will not go to great heights or depths, but you will have to walk over very rough
surfaces). The fractal dimension of these landscapes is related to the exponent d;
larger d correspond to smaller fractal dimensions.
Click on the image for a larger view. Note that the z-scale is not the same for all images.
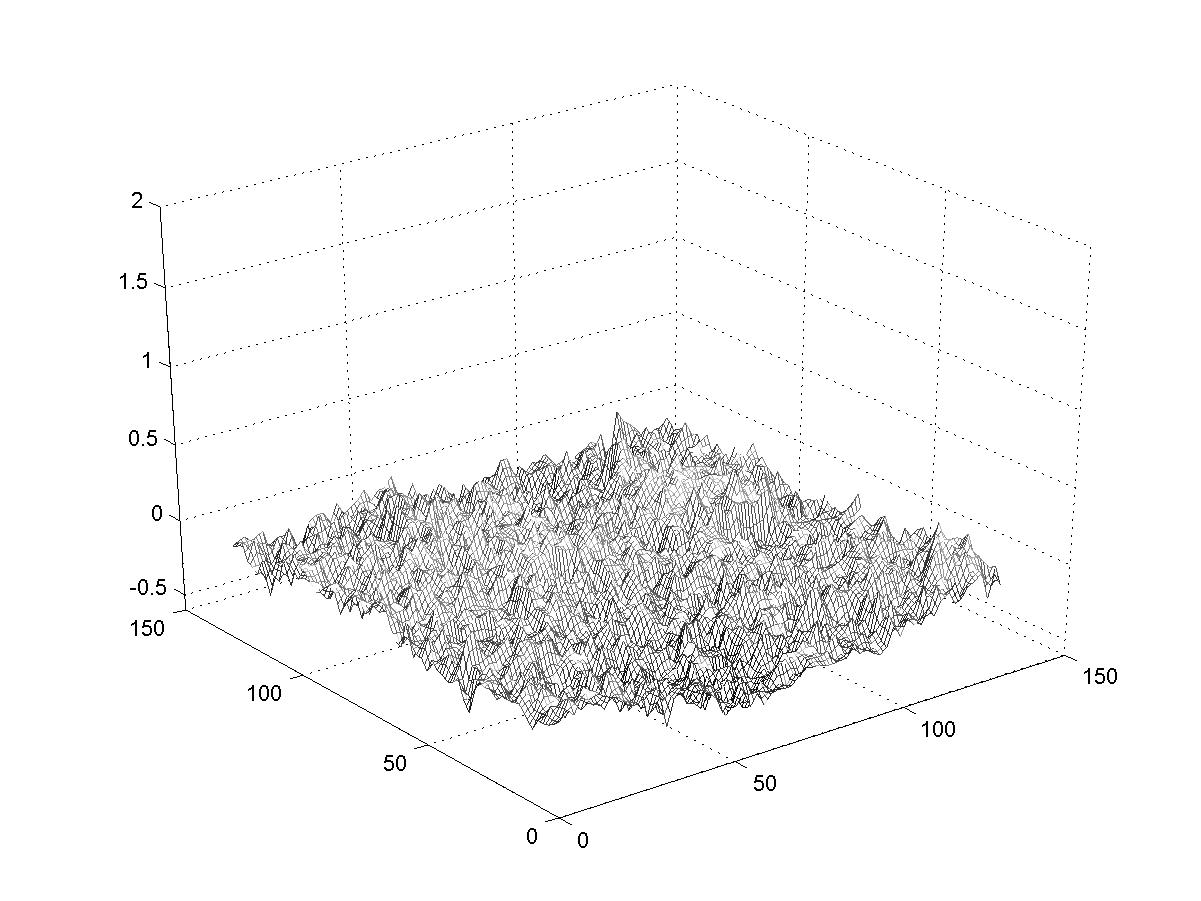
d=0.1
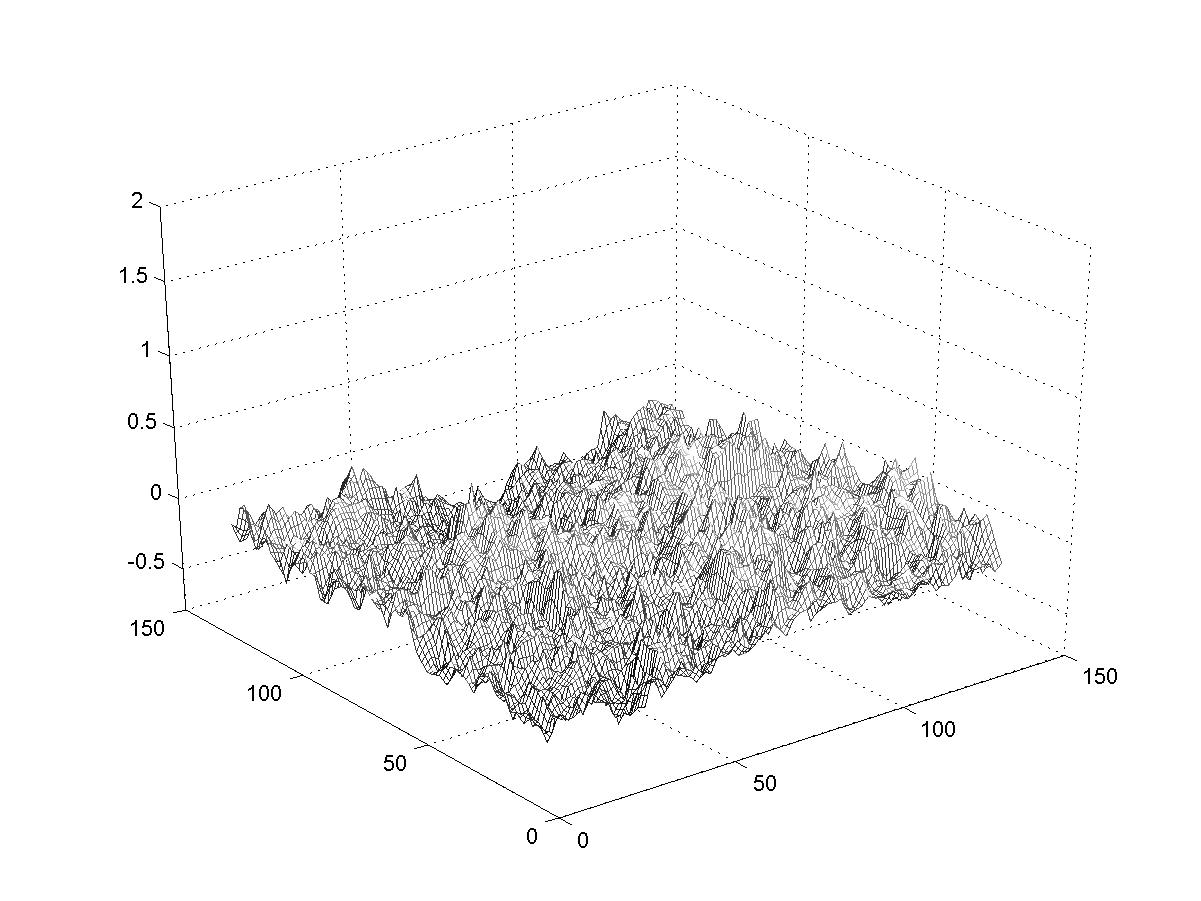
d=0.3
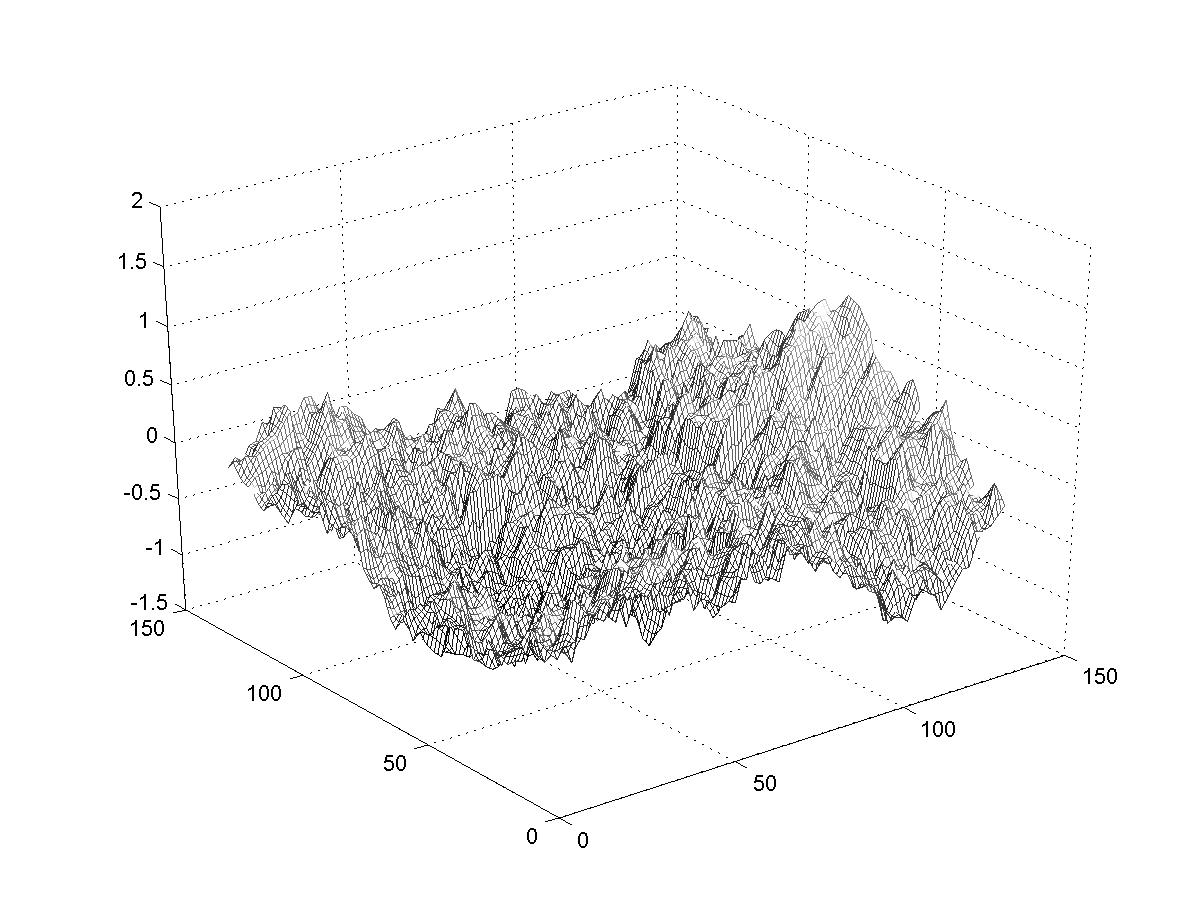
d=0.5
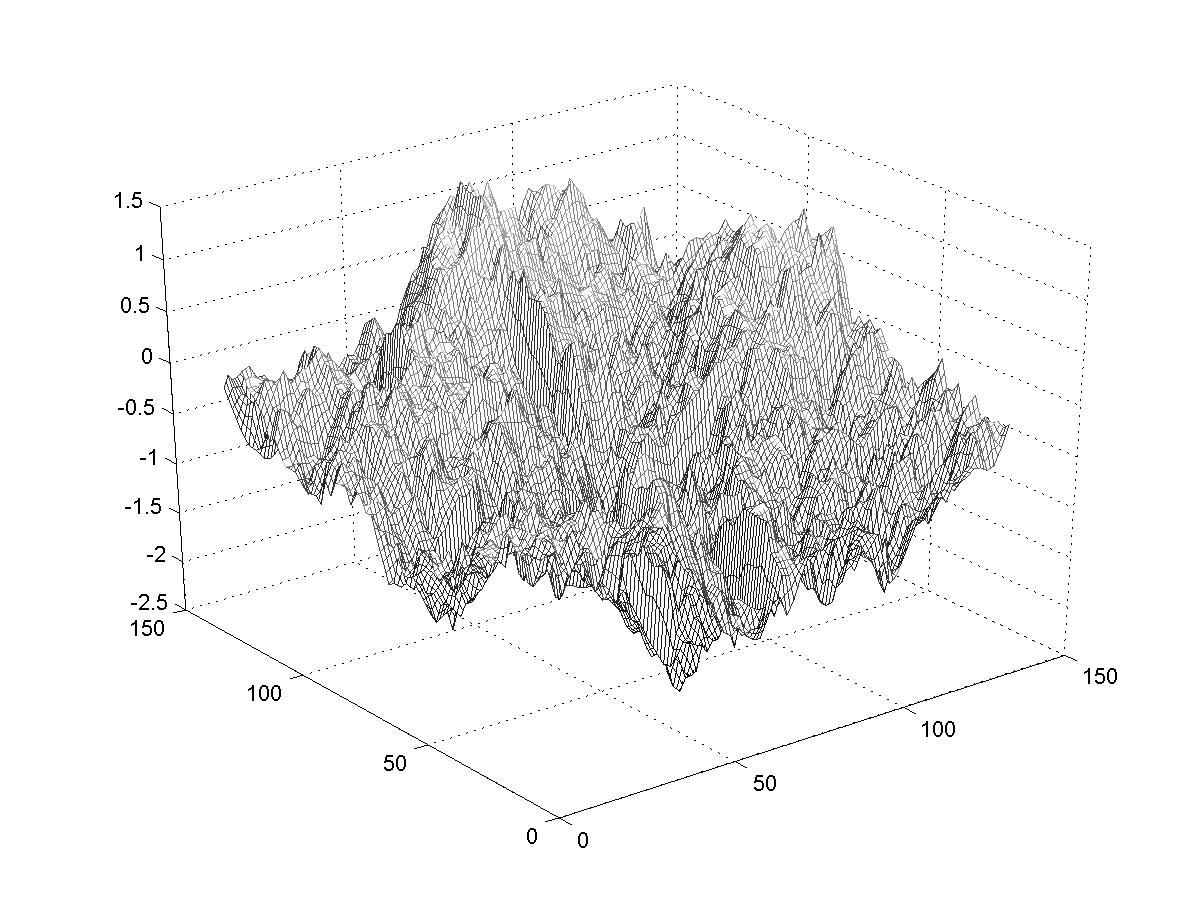
d=0.7
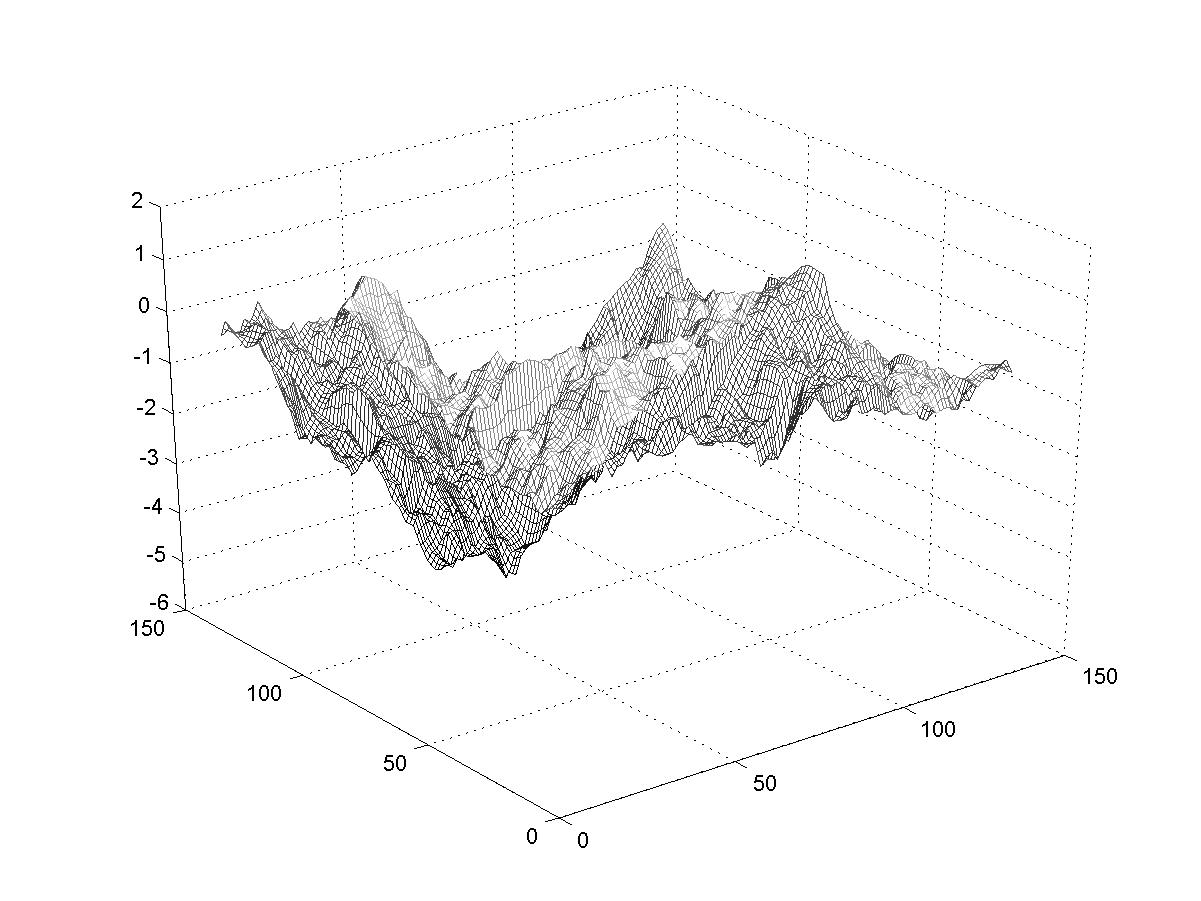
d=0.9
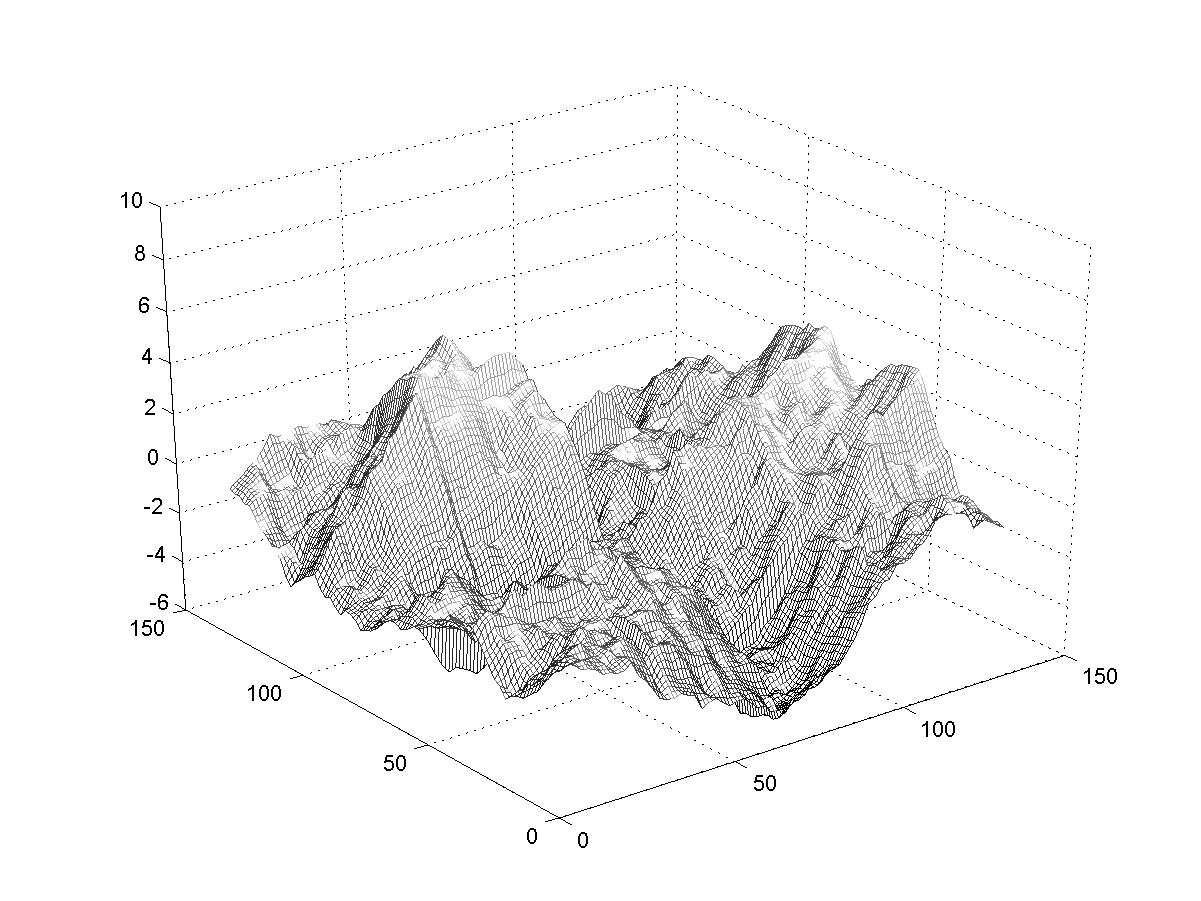
d=.11

d=.13
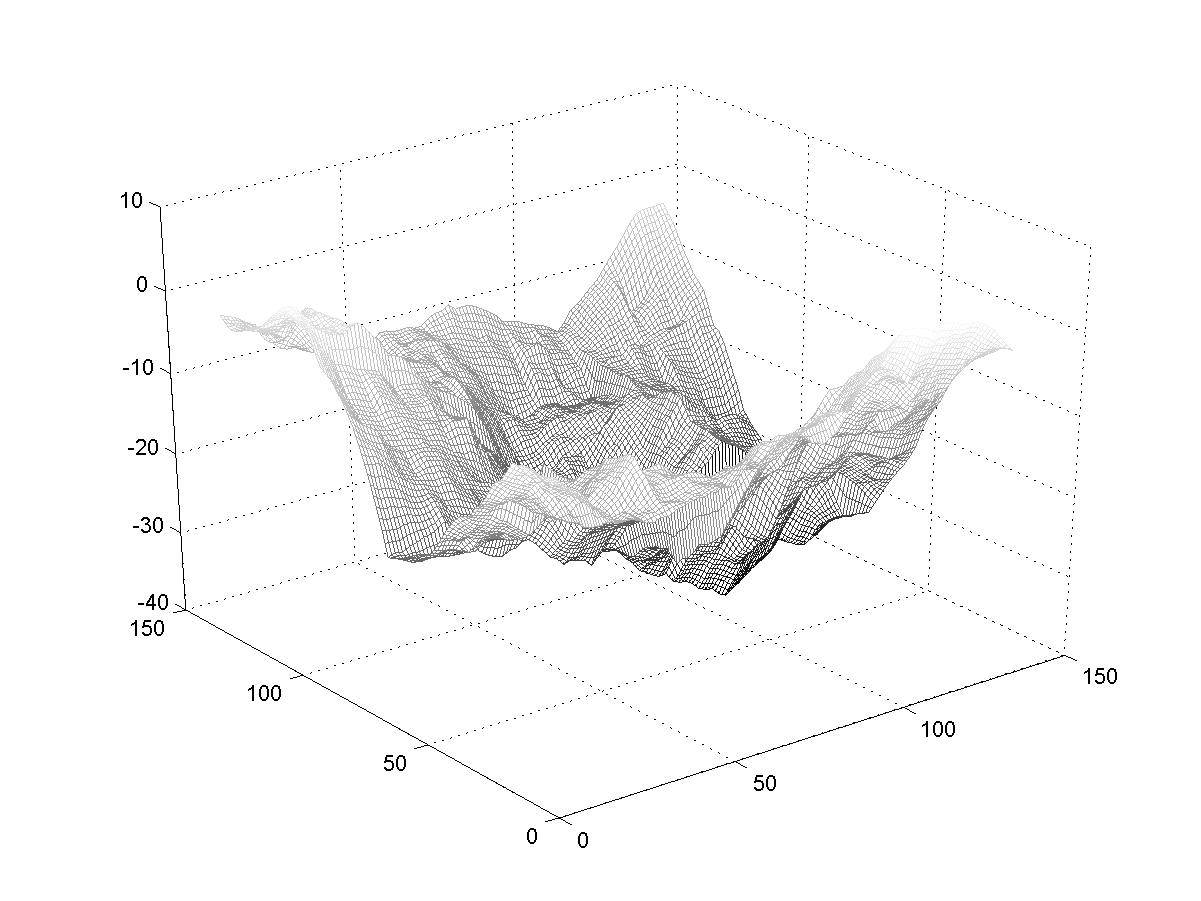
d=.15
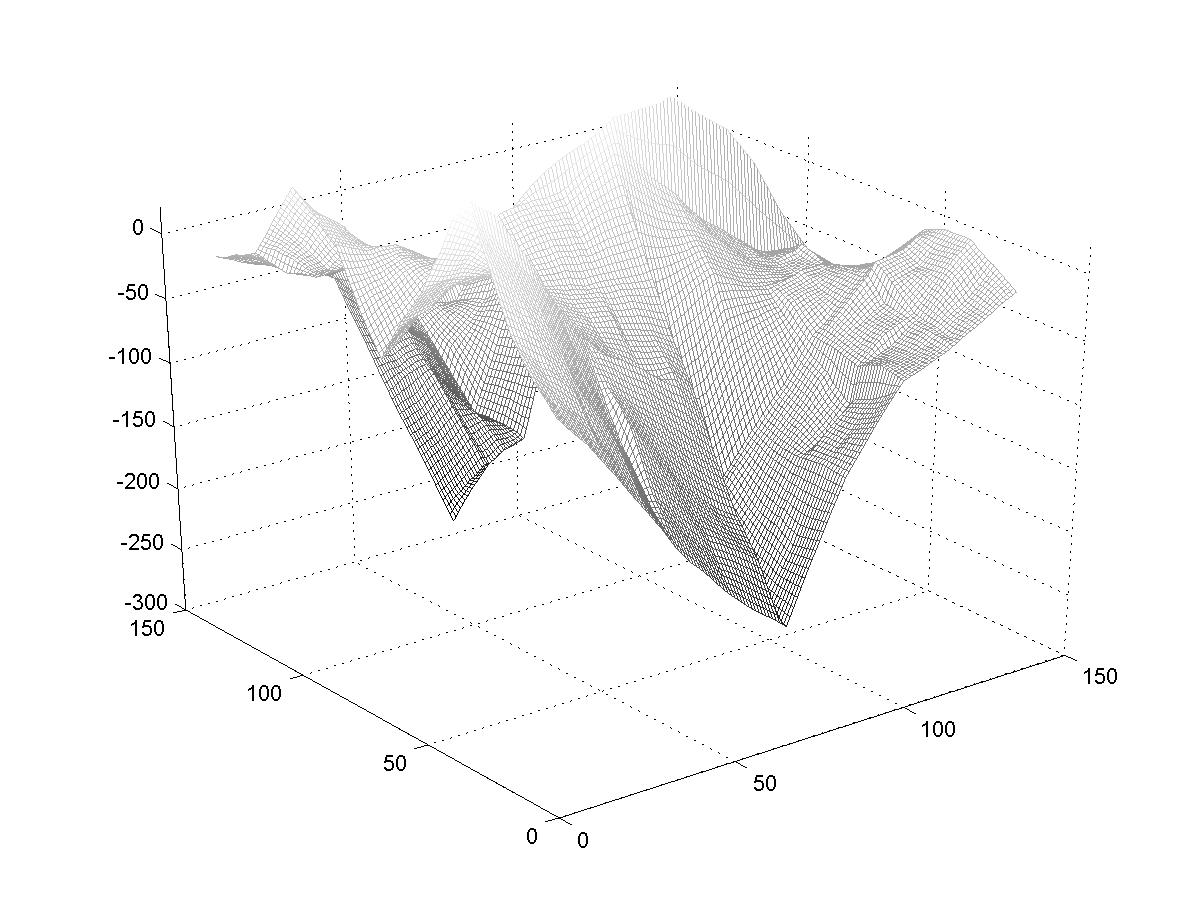
d=2.0








