Figure 1
PASCAL'S TRIANGLE IN ALGEBRA
The arithmetic triangle is composed of the coefficients of the polynomial (1+x)n in a triangular array. Here n denotes the row number starting from n=0, with n+1 entries in each row.
|
Example 1: |
(1+x)4 = 1 +4x + 6x2 + 4x3 + x4 is a polynomial in the 4th row, 5 entries with coefficients from left to right: 1, 4, 6, 4, 1. (Refer to Figure 1 below) |
Figure 1
Alternately, the coefficients of the nth row can be determined by the coefficients of the (n-1)th row.
Example 2: In the 3rd row, the entries are 1, 3, 3, 1, and the 4th row with 1, 4, 6, 4, 1. (See figure 2)
Note that the outside diagonals in the triangle are always the entry 1. Then the entry 4 is from (1+3 = 4), the 6 is from (3+3 = 6) and the 4 is from (1+3 =4).

Figure 2
PASCAL'S TRIANGLE IN PROBABILITY
Pascal's Triangle can answer questions such as "How many different ways can a person pick k item(s) from n number of items?" You may recall this is the choosing property in Probability.
Example 3: How many ways can I choose 2 hats out of 5 hats despite the order of the 2 chosen hats?
This implies "5 choose 2", and the answer is located in the 5th row, 2nd entry of Pascal's Triangle. Note that at the very top of the Triangle, that entry is "row 0 and 0th entry". (See Figure 3 below) Therefore, 5C2 = 10.

Figure 3
 CLICK PICTURE ON LEFT FOR MORE ROWS OF PASCAL'S TRIANGLE!!
CLICK PICTURE ON LEFT FOR MORE ROWS OF PASCAL'S TRIANGLE!!
NEW COORDINATE SYSTEM FOR PASCAL'S TRIANGLE
Pascal's Triangle has its own set of coordinate systems. Here's how you would set up the coordinate system:
|
Steps: |
1) |
Start with the origin (0,0) as the top entry (1) in a triangular array. |
|
|
2) |
Let the x-axis run diagonally to the left and the y-axis diagonally to the right. |
|
|
3) |
Then each pair of coordinates (x,y) corresponds to a specific location in the array. (Refer to figure 4 below) |
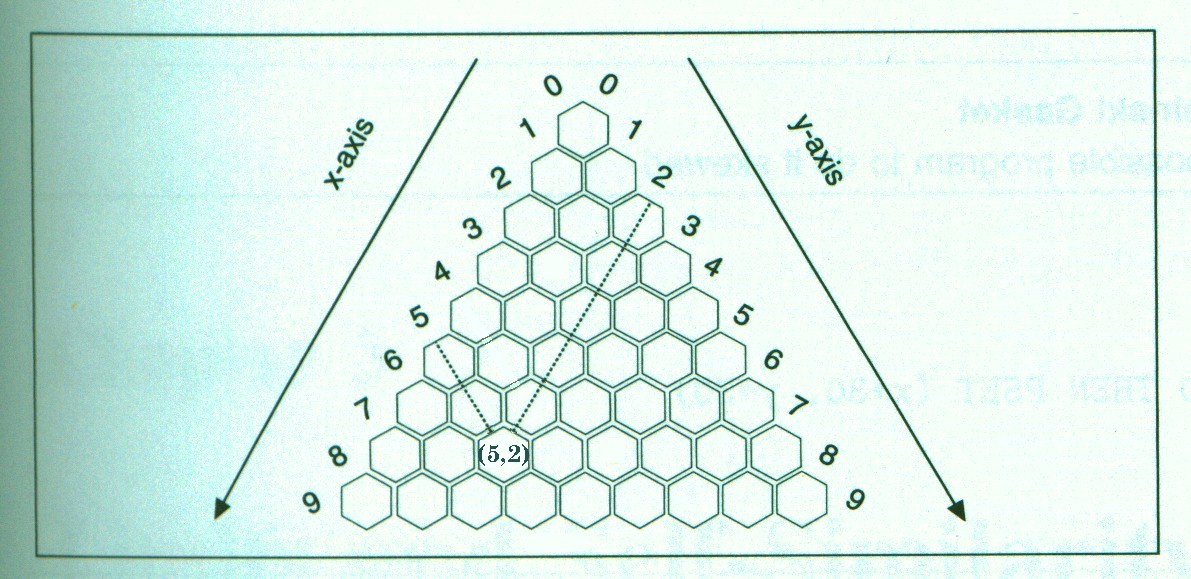
Figure 4
Note: Wherever there's a 1 in Pascal's Triangle, then either the x-coordinate is 0 and/or the y-coordinate is 0. Figure 4 shows the position of (5,2). (More on this new coordinate system will be discussed later with IFS.)
FORMING SIERPINSKI'S TRIANGLE BY COLOUR CODING
Besides forming a pattern with polynomial expansions, colour coding Pascal's Triangle forms neat different patterns. When we colour the even coefficients in white and the odd ones in black, we have actually formed the Sierpinski's Triangle. (See figure 5)

Figure 5
FORMING SIERPINSKI'S TRIANGLE BY BINARY EXPANSIONS
Besides finding the pattern of Sierpinski's Triangle by colouring the even numbers white and the odd numbers black in Pascal's Triangle, there is an alternate method avoiding the calculations of each row's coefficient, using its coordinate system. To determine the colour of (x,y), place the binary expansion of the two coordinates on top of each other. If two 1's appear in any column, then the cell of coordinate (x,y) is coloured white; otherwise, black.
|
Example 4: |
We want to determine the cell colour of (3,4). |
|
|||
|
|
In binary expansion, it is (011, 100). |
|
|||
|
|
Put them on top of each other: |
011 100 |
|||
|
|
Two 1's do not appear in the any columns, so this cell is coloured white. |
|
|||
OTHER PATTERNS IN PASCAL'S TRIANGLE
Other interesting patterns are formed when we divide the coefficients in Pascal's Triangle by divisors such as 3, 5, or 9. I was able to find a very good program from the Internet that can perform the patterns with many modulus (See link below). For instance, when we take 3 as the divisor or modulus and replace the coefficients by the remainders (0, 1, or 2) after dividing through by 3, and a new pattern is formed. The more rows we use, the more visible the pattern.
![]() program needed to run the applet (just have to download, don't need to run)
program needed to run the applet (just have to download, don't need to run)
![]() the applet (run this .exe file after downloading the above program)
the applet (run this .exe file after downloading the above program)
![]() downloading instructions and program instructions
downloading instructions and program instructions
WHAT IS SELF-SIMILARITY?
By definition, "Two objects are similar if they have the same shape regardless of their size. Corresponding angles, however, must be equal and corresponding line segments must all have the same factor of proportionality." (Peitgen et al, pg.138) Thus, self - similarity is when you enlarge a small part of the overall pattern, you will see the exact same overall pattern. In other words, the overall pattern is composed of many of these small self-similar patterns.
SELF SIMILARITY IN SIERPINSKI'S TRIANGLE
When we extend Pascal's Triangle mod 2 version to infinitely many rows, and each time we double the number of rows, we reduce the triangle by a scale of 1/2, then the resulting design is a self-similar Sierpinski's Triangle. In other words, if we magnify a subtriangle, we see a reproduction of the whole Sierpinski's Triangle. In fact, each of the patterns described above with different divisibility of Pascal's Triangle produces a self - similar pattern too.