Virtual Library of Simulation Experiments:

Screening Test Problems

---

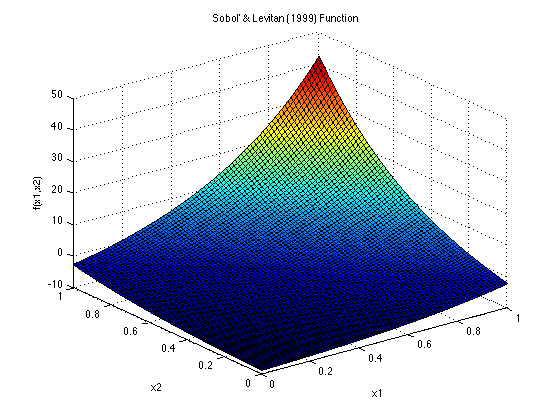
Sobol' & Levitan (1999) Function

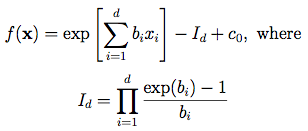
Description:

Dimensions: d

The Sobol'-Levitan function . The value of the elements in the b-vector (b₁, …, b_d) affect the importance of the corresponding x-variables.

Moon et al. (2012) scale the output to have a variance of 100. For d = 20, they use three different b-vectors:
(2, 1.95, 1.9, 1.85, 1.8, 1.75, 1.7, 1.65, 0.4228, 0.3077, 0.2169, 0.1471, 0.0951, 0.0577, 0.0323, 0.0161, 0.0068, 0.0021, 0.0004, 0),
(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0), and
(2.6795, 2.2289, 1.8351, 1.4938, 1.2004, 0.9507, 0.7406, 0.5659, 0.4228, 0.3077, 0.2169, 0.1471, 0.0951, 0.0577, 0.0323, 0.0161, 0.0068, 0.0021, 0.0004, 0).

Sobol' & Levitan (1999) use two different b-vectors:
(1.5, 0.9, 0.9, 0.9, 0.9, 0.9), for d = 6, and
(0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4), for d = 20.

The generally used value of c₀ is c₀ = 0.

The plot above shows the two-dimensional form of this function, with b = (2, 1.95) and c₀ = 0.

Input Domain:

The function is evaluated on x_i ∈ [0, 1], for all i = 1, …, d.

Code:

References:

Moon, H., Dean, A. M., & Santner, T. J. (2012). Two-stage sensitivity-based group screening in computer experiments. Technometrics, 54(4), 376-387.

Sobol', I. M., & Levitan, Y. L. (1999). On the use of variance reducing multipliers in Monte Carlo computations of a global sensitivity index. Computer Physics Communications, 117(1), 52-61.

---

For questions or comments, please email Derek Bingham at: dbingham@stat.sfu.ca.