|
Beyond Experience: Metaphysical Theories and Philosophical
Constraints, Second Edition, Copyright © Norman Swartz, 2001.
Available for downloading, free of charge, at http://www.sfu.ca/~swartz/beyond_experience. {page 24} CHAPTER THREE Theories: What they are and what they are not In chapter 2, I invoked the concept of theory several times. In chapters 4 and 5, I will discuss what differences there are between metaphysical theories and scientific theories and what the problems are in generating and testing theories. But we will pause here to examine the concept of theory itself. A theory is, in the broadest sense, one or more hypotheses about some particular subject matter, such as mechanics, optics, international trade, disease transmission, learning, pest control, ethics, infinite numbers, or sexual maturation. A theory is, in brief, an attempt to come to grips with, to make sense of, to explain, and in some instances to control and predict, something of particular interest to us, often some feature of the world (children's growth, climatic changes, audio reproduction, etc.), but sometimes something as 'abstract' as provability or existence in mathematics. On this account, we all construct theories constantly. Some of them may be relatively long-lived; for example, you might theorize that investing one-tenth of your net income in government bonds is the best manner to save for your retirement and might subscribe to this theory and put it into practice (follow its precepts) for all of your working lifetime. Other theories might be rejected almost immediately; for instance, the theory that the noise in a distant part of your friend's apartment was caused by someone's knocking on a window. It may happen that no sooner does this theory cross your mind than it might immediately be discarded, particularly if you happen to recall that you are visiting in an apartment on the forty-second floor. It might strike you as rather overstated, even a bit pretentious, to call a momentarily entertained belief that someone is knocking on the window a "theory". You may find that you want to reserve the term "theory" for something somewhat more elaborate, more specialized – {page 25} for example, a theory about chemical reactions, or immunization, or electromagnetic radiation. You might, that is, be inclined to reserve the term "theory" exclusively for recognizably scientific contexts. But there is no particular need to be diffident about conceiving of commonplace, even momentary, beliefs – e.g. about the cause of a noise in an apartment – as theories. Scientists have no more proprietary claim to "theory" than they have to terms like "experiment", or economists have to terms like "profit". To be sure, there is, for example, a specialized sense of "profit" which economists adopt in their economic writings, but that sense is certainly not the only viable sense. We can, and do, for example, talk about the profit, not monetary or capital gain certainly, in reading a good book, or taking a vacation, or quitting smoking. There unquestionably is this more general notion of "profit" having to do with gaining a good of any sort. So too is there a notion of "experiment" which includes, but is not restricted to, the kinds of deliberately crafted laboratory experiments conducted by scientists. The four-year-old child, in rubbing one crayon over a mark made by another crayon, is experimenting with colors and textures; a chef substituting one spice for another specified in a recipe is experimenting with flavors; and so on. And so it is with the term "theory". Theorizing is not something confined to the scientific context, nor is it the sole preserve of the trained scientist. All of us theorize. We theorize about the cause of the delay in the mail, the best way to handle the grievance from the shop steward, whether there is an afterlife, how to avoid having to buy a new vacuum cleaner, whether it would be profitable to search the house for our missing notes for the report we are writing or whether to assume that they are forever lost and it would be best to try to reconstruct them, etc. (You may recall, a moment ago, at the very end of chapter 2, I wrote: "Frequently, I will venture to say something bolder, to wit, something tantamount to, 'This is the way such-and-such a concept ought to be understood.' When I do that, I will not merely be reporting how the concept is used; I will be suggesting how we might profitably revise or refine our concept for further use." Notice that this is precisely what I have just been doing, in discussing how the concept of theory is to be understood, and I will continue to do so throughout the rest of this current chapter. I am not merely saying that such-and-such is the way the concept theory is used; I have been arguing, and will continue to argue, that to adopt a certain usage is useful and profitable. In short, I am not just engaging in a piece of descriptive {page 26} lexicography,*1 but I am here doing philosophy, in this particular case, recommending how we might best, or at least usefully, regard the concept of theory. I have, that is, started upon a philosophical theory about, interestingly enough, the very concept of theory itself. Hereinafter, however, as I continue this sort of exercise for a variety of other concepts, I will not again explicitly direct your attention to the fact that I am not only reporting how a concept is ordinarily used, but also, and more importantly for my purposes, making a proposal how I think it might better be used. Concepts, after all, are intellectual tools. We are not duty-bound to leave them as we find them. We are entitled to tamper with them, to experiment with them, in an effort to try to improve them. And having wrought modifications in a concept, we are entitled to offer those changes to others, along with our reasons for the revisions and with samples of their uses, so that others may have grounds for accepting, rejecting, criticizing, or modifying our handiwork in turn.)
Some authors like to make a distinction between hypotheses on the one hand and theories on the other. The distinction is akin to that between sentences and paragraphs: a paragraph may consist of a single sentence, but it may also consist of a great many sentences grouped together by a common subject matter. Similarly, a theory may consist of a single hypothesis, but it may also consist of a great many hypotheses grouped together by a common subject matter. Because theories are, in the end, collections of one or more hypotheses, I will not usually distinguish between the two. I am as happy to talk about hypotheses as I am about theories. A theory, on this account, is a guess, sometimes a remarkably insightful guess, sometimes one containing several propositions*, but a guess, hypothesis, or conjecture nonetheless. I use all these terms, "guess", "conjecture", and "hypothesis", almost interchangeably. The only difference is that while all hypotheses are guesses, not all guesses are hypotheses. A child may hide a jelly bean in one of her fists and ask her brother, "Which one?" If the brother tries, using his knowledge of his sister's typical behavior, to figure out in which hand she is likely to have concealed the candy, then he is constructing a hypothesis. But if he chooses at random, makes a stab in the dark as we say, he is merely guessing, not hypothesizing. The difference is that a hypothesis is something more, but often little more, than just a guess. {page 27} It is an attempt to make sense of, or to predict the truth of some feature of the world by calling upon one's prior knowledge of the world and some rational grounds for expecting it to be of one sort rather than another. But with this said, I will not trouble myself further with trying to offer a decisive account of the difference. Guesses and hypotheses are similar enough to one another that – for present purposes – a precise account of their subtle differences is not required. Some theories – e.g. that someone is knocking on the window – may be regarded to be among those things which may be judged true or false. But other theories do not lend themselves to being judged true or false – e.g. the theory (next chapter) that we should prefer explanations of natural events in terms of causes rather than in terms of purposes. These latter sorts of theories must be judged on other criteria; for instance, Is the adopting of the theory useful? Does it allow us to get on better than do alternative theories? Is it simpler than alternative theories? We will return to the matter of appraising such theories later, in chapter 6, where we will examine metaphysical theories in greater detail. Theories of the sort which allow for being judged true or false do not cease to be theories when their truth or falsity becomes known. A theory – just like a guess – may be true; equally well a theory may be false. This is not to say of course that any one theory may be both true and false. I mean simply that something's being a theory does not preclude its being true: it may be, or then again, it may not be. And thus a theory does not cease to be a theory when its truth comes to be regarded as a virtual certainty. Geometrical optics is sometimes held up as an example of a body of knowledge whose truth is a practical certainty and whose details have been agreed upon, virtually without change, for more than one hundred years. But despite its durability, it is still appropriate, within the meaning of the term, to call geometrical optics a "theory". So, too, is it appropriate to talk of the theory that poliomyelitis is caused by a virus. This latter claim is, so far as I know, universally assented to within the medical profession. But it is still perfectly appropriate to call the claim a theory. I emphasize the point that a theory may be true, that this is no contradiction in terms, because there is a bogus, quasi-political, argument to the contrary which we would do well to scotch. Some creationists have argued that Creation Science deserves to be taught in the public schools alongside evolutionary theory, because both are conjectures and neither can be regarded as established fact. The flawed argument runs like this: "The very name 'evolutionary {page 28} theory' signifies that the claims being made are not proven. Whatever is proven is called a 'fact', not a 'theory'. Evolutionary theory is not proven. It is conjecture; it is a set of beliefs. But insofar as evolutionary theory is just that, a theory, i.e. unproven, then so too does creation theory, admittedly also not proven, deserve to be taught alongside as an alternative viewpoint." The creationist has in this argument made heavy weather of the word "theory", stating explicitly that the term implies "not proven". This is simply incorrect. It is perfectly proper to regard a body of propositions which have a certain explanatory power, and which are generally regarded as true, as a "theory". Witness: the special theory of relativity, today so well established that it is not much challenged; the theory of conic sections, believed by most, if not all, mathematicians to be absolutely correct and not profitably to be challenged; and the theory of logarithms. All of these are theories, and all of them – just like the previously mentioned theories of poliomyelitis and geometrical optics – are reasonably to be regarded as true.2 If espousers of Creation Science, then, want to make a case for the teaching of Creation Science in the public schools, they must do so on grounds other than the claim that evolution and creation are both theories. For, from the fact that something is a theory, nothing whatsoever follows about its worthiness, or unworthiness, to be taught in the public schools. Whether Creation Science deserves to be taught depends, rather, on what kind of theory it is: for example, whether it is religious or scientific, whether it is amenable or immune to revision, and whether it is strongly or weakly confirmed* by the evidence offered in its support.
Theories which are true or false are called "truth-valued theories". (Being "truth-valued" simply means being "either true or false".) Among truth-valued theories, just as some may, with virtual certainty (conviction), be regarded as being true, others may, with equal certainty, be regarded as being false; e.g. the theory that flies spontaneously generate from putrefying meat; the theory that human beings are the only tool-making animals on this planet; and the theory that it is possible to construct a perpetual-motion machine. But most truth-valued theories fall somewhere between the two extremes, some close to one end or the other, while other theories fall closer to the middle. {page 29} This is not, of course, to say that truth-valued theories fall along a continuum from true to false. There is nothing 'between' truth and falsity. Any truth-valued theory is either true or it is false; there is no other alternative. There is, however, a continuum between our attitude of resolute conviction on the one extreme and our attitude of total disbelief on the other. We may well be strongly inclined to view some particular theory as true, another theory as false, and still another as one whose truth or falsity we are unsure about. Thus it is possible, although relatively rare, to be badly mistaken about a theory's truth. We might, for example, take a false theory to be indubitable, even though – in this case – we happen to have made a mistake, and the theory is, in fact, false. As human beings, wanting to get on in the world, we must make reasoned judgments about the truth or falsity, or the utility as the case may be, of many of our theories. We may, even, feel ourselves justified in adopting an attitude of certainty about particular ones among our truth-valued theories. On occasion, however, the world fools us; on occasion, the world surprises us. What we are convinced is true sometimes turns out – for all that – to be false; and what we are convinced is false sometimes turns out – for all that – to be true. In the previous chapter I mentioned that many persons hold to a variety of theories without even being aware that they do so. I think, in fact, that we each hold not to just a few such theories, but to a great many. These theories typically are not especially well-articulated. Indeed, I am sure that most of the theories each of us subscribes to are held rather inchoately, below the level of conscious examination. Not only are we often not aware that we hold them, we would have some difficulty in articulating them were we to try. The case is analogous to a person's knowing the meaning of a word, but without being able to give a definition of that word. This is especially true of children. Children know, that is, are able to use correctly, a great many words. But they are not able to define those words or tell you what those words mean. Being able to use a word and being self-consciously aware of the meaning of the word are two quite different skills. The latter comes only later in one's intellectual development, if it comes at all. Similarly for theories. Each of us subscribes to an enormous number of theories but we may be totally unaware that we do, and may be unable to articulate many of the theories we in fact believe and act upon. Theorizing begins at a very early age. Even as the young infant lies in her crib, she begins exploring her environment and theorizing {page 30} about it. Laboratory data suggest that it takes some weeks before the infant 'catches on' to the fact that when objects pass out of view (e.g. Mother or Father leaving the room) or one object passes behind another object, the obscured object does not 'go out of existence' ([115], 451-3). But what exactly do we mean when we say that the infant 'catches on' to the fact that most material objects persist (continue to exist) even though obscured from view by some other physical object? The most natural way to explicate this notion of 'catching on' is to say of the infant that she has posited* the hypothesis (constructed the theory) that obscured physical objects continue to exist, and that, by experimenting, has come to accept this hypothesis. Note, of course, that we are not saying that the infant has a concept of hypothesis or of theory. One may create a theory without having the concept of a theory, just as one may walk or talk without having the concept walking or the concept talking. And it bears remarking, too, that some theorizing at least – for example, this very case of the young infant hypothesizing the persistence of obscured physical objects – can proceed without a language. Indeed animals which lack languages can also be regarded as engaging in theorizing, although at a much less sophisticated level than human beings. Just as animals, e.g. cats and dogs, can be regarded as having certain kinds of unsophisticated beliefs, they can as well be regarded as engaging in a kind of low-level, unsophisticated, theorizing.3
In the eighteenth century, Kant hypothesized (recall the second quotation from Buber in chapter 2, p. 12) that the human mind is so constituted as to interpret the data of our senses in such a way that the external world would present itself to our consciousness so as to be perfectly describable by Euclidean geometry. If someone were to try to salvage this theory, and render it in a more modern idiom, it would probably emerge as the theory that our brains are hard-wired (preprogrammed) to apply a Euclidean computation to the data provided by {page 31} our sensory organs. Modern engineers use the technical term "filter" to describe any 'black-box device' which alters, in a determinate manner, signals or information passing through that device ([102], 352). Thus polarizers placed on a camera lens are filters, but so too are bass and treble controls on a stereo amplifier, and so too are many computer programs, e.g. ones which chop text files into readable chunks of twenty-five lines, or which justify lines of text so that they are all of uniform width on a page. In modern terminology, then, Kant's theory was that the mind acts as a filter on the raw data of sense to transform them in such a way as to conform to the calculus of Euclidean geometry, or to put it still another way, the mind is itself a Euclidean filter. Now this particular claim, both in its original form and in its modern transformation, is probably false. We probably are not preprogrammed to view the world with the kind of specificity inherent in Euclidean geometry. We may not, that is, be preprogrammed to interpret the world so that, for example, doubling the lengths of the sides of a triangle would leave all the angles unchanged. (This latter is a theorem of Euclidean geometry, but not of some other geometries.) But we may be preprogrammed to interpret the world in more general ways, e.g. to conceive of it as having movable, enduring, physical objects; or to conceive of it as having objects at varying distances from our personal loci of perception. Since the early-twentieth century, some experimental psychologists and linguists have turned to examine these sorts of questions empirically: What sorts of beliefs, if any, do we seem predisposed to adopt? What sorts of concepts, if any, do we seem naturally to use? Some of the pioneering work in this field, in particular Piaget's investigations into children's understanding of the concept of causality, remains among the most interesting and philosophically illuminating ([152]). His experimental data showed that children take several years to develop anything like an adult's understanding, and use, of the concept of causality.4 Perhaps this very fact that it takes children so long to master the concept of causality may help to explain why philosophers have had such a difficult time in trying to explicate it. The concept of causality may take so long to acquire because it is so complicated {page 32} and multifaceted, and indeed probably is not one single concept, but rather a family of concepts.
It should be clear, from the examples I have been giving, that theories need not be (sets of) mathematical formulas. Certain philosophers, however, in trying to explicate the concept of a theory, have focused their attention on the sorts of theories one finds in physics and chemistry. For example, Ernest Nagel, taking his inspiration from Norman Campbell (1880-1949), writes: For the purposes of analysis, it will be useful to distinguish three components in a theory: (1) an abstract calculus that is the logical skeleton of the explanatory system, and that "implicitly defines" the basic notions of the system; (2) a set of rules that in effect assign an empirical content to the abstract calculus by relating it to the concrete materials of observation and experiment; and (3) an interpretation or model for the abstract calculus, which supplies some flesh5 for the skeletal structure in terms of more or less familiar conceptual or visualizable materials.
By an "abstract calculus", Nagel means a mathematical equation or a statement expressed using the symbolism of modern mathematics or logic, e.g. (3.1) F = ma (3.2) I = E/R (3.3) Z = 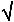 [R2 +
(XL – XC)2] [R2 +
(XL – XC)2]
Such symbolic expressions are, in the first instance, to be conceived only as formulas which may be manipulated by the rules of some system. The "F", the "m", the "a", etc. are to be regarded merely as variables, in much the same way that a high-school teacher may {page 33} instruct students to manipulate expressions in algebra, such as To be fair, Nagel explicitly denies that this philosophical reconstruction which he is offering is meant to portray precisely what you might expect to find in physics texts and journals, nor is it meant to capture the "actual stages in the construction of theoretical explanations". Nagel's explication, which is promoted by a great number of other philosophers of science as well, is intended to reveal no more and no less than the 'logical structure' of scientific theories. Philosophical 'reconstruction' is a peculiar business. Even among philosophers who nominally belong to the same school of philosophy, there are remarkably different opinions as to what, properly, ought to go into a philosophical reconstruction. Nagel,6 in this passage, has allied himself with the so-called formalist branch of Analytic philosophy. The formalist approach may be contrasted with the contextualist (or ordinary-language7) approach. The differences between these two approaches were more clear-cut and topical in the 1950s than they are currently, but something of the attitudes each wing took toward philosophy still characterizes many contemporary philosophers. Although {page 34} not pledging unreserved allegiance to either wing, many contemporary philosophers tend to identify more strongly with one approach than with the other.
On the matter of explicating the concept of theory, I depart widely from the formalists. To focus exclusively, or even primarily, on the mathematical and logical features of certain refined theories in physics, chemistry, and economics strikes me as drawing too restricted a sample and ignoring too many other critical features. Of course some theories are highly mathematical (quantum theory, special and general relativity, string theory [in cosmology], etc.), but this must not cause us to overlook that the greatest number of our theories are not mathematical ones. We will fail to understand what role theories – both scientific and metaphysical ones – play in our lives if we blinker our analysis by conceiving of theory overly narrowly. Theorizing permeates our human approach to the world. It is not something reserved exclusively for the accomplished, trained scientist. All of us theorize constantly, on political matters, human relationships, humankind's place in the world, children, earning a living, friendship, loyalty, death, etc. Philosophers differ, too, as to whether, and how much, a philosophical analysis ought to try to capture the route or means by which a concept is acquired. Formalists will usually dismiss the matter of concept- and theory-generating as 'psychologizing', arguing that it has no proper place in the concerns of philosophy. Again others, I among them, take the opposite point of view. Pick up any textbook which attempts to teach a person physics or chemistry. The actual mathematical formulas typically will comprise no more than 5% of the total text, in some books vastly less, perhaps no more than 1%. Attend some introductory classes in any science, whether physics, chemistry, economics, sociology, or anthropology. There you will hear the lecturer speaking almost entirely in English or some other natural language. Usually the lecturer will write down the mathematical parts of the lecture on the blackboard, and students will copy that math into their notebooks. An outsider, looking at those class notes, might easily mistakenly infer that the lecture was almost entirely in mathematics. But this is clearly not so. To teach a theory, to explain it to other persons, to get those other persons to understand the theory – so that they in turn can use it, can apply it to the world in an attempt to understand, manage, and predict what is going on in the world – one must communicate in a natural language. We never learn theories by first being taught an uninterpreted calculus, and then, {page 35} having mastered the manipulation of the symbols, by being informed, at a second stage of initiation as it were, what those symbols refer to. No, teachers first try to explain to their students what the concepts of (for instance) mass, profit, capital, velocity, and neurosis are, and then and only then do they proceed to introduce symbols for those concepts. To understand why the formalists find the sort of analysis offered by Nagel both alluring and plausible, one must understand that this sort of analysis has had some very striking historical successes. It is, to my mind, still the best account available to explain how it is possible that there can be alternative geometries. For two thousand years, from the time of Euclid to the mid-nineteenth century, there had been but one geometry: Euclid's. The prevailing view as to why there was exactly one geometry was to the effect that, in some sense, either because geometry was a logical necessity or because geometry was imposed by the mind on the data of sense (Kant), there could not be any more than one. When, finally, several geometries were discovered (invented) which competed with Euclidean geometry, an explanation had to be found. The sort of analysis offered by Nagel and other formalists serves that purpose admirably. By conceiving of each and every geometry as, in the first instance, consisting of just a set of uninterpreted formulas, the way was found to place them all on an equal footing. All geometries are simply abstract, uninterpreted calculi saying nothing whatsoever about the real world, and thus none of them is either true or false. Only when an uninterpreted system is 'fleshed out' with an interpretation, for example, linking the uninterpreted term "L" with something in the actual world that is to count as a line, can the interpreted geometry thereby created then be tested for truth or falsity. Thus the model Nagel presents is powerfully historically motivated. It has had some stunning success. And indeed I continue to use it regularly to explain to my own students how it is possible that there are bona fide alternative, non-Euclidean, geometries. But the question remains as to how far this particular formal analysis of theory may be extended. And it is in answering this question that some of the most fundamental differences in philosophical attitude become vocally contested among analytic philosophers. Plato is reputed to have had inscribed in the lintel of the entrance to his Academy the motto "Let no one who is not a geometer enter." The slogan had a point. Plato looked upon geometry as the 'ideal' of knowledge. It was the 'most perfect' form of knowledge. Non-geometrical {page 36} propositions were regarded as approximating to knowledge to the degree that they exhibited the rigor and style of geometry. To be sure, there is something quite remarkable, audacious, even aesthetically pleasing, that is to say, beautiful, in geometry. It is a marvel of the powers of human reason. But to what extent any given masterpiece, whether a geometry, a musical composition, or an act of bravery, ought to set the standards by which others of that genre are to be judged remains an issue over which all of us, philosophers and non-philosophers alike, will perennially argue. Nagel and other formalists tend to offer specific, idealized, reconstructions of many of our most fundamental concepts – e.g. of theory, of cause, of explanation, indeed even of space and of time8 – growing out of analyses of some especially favored particular cases. Carl Hempel, for example, in explicating the concepts of theory, cause, and explanation ([90]), invoked the case of a car's radiator cracking when the temperature fell below freezing – a case lending itself to prediction by citing antecedent conditions (drop in temperature, lack of antifreeze, etc.) and known scientific laws (concerning the expansion of water when frozen, the tensile strength of metals, etc.).
Non-formalists are temperamentally disposed to cast their nets far wider, to collect a much greater diversity of cases from which to begin and then to try to accommodate as much as possible of this diversity in their analyses. Critics of the formalist approach will argue, for example, against the appropriateness of Hempel's favored example, objecting that it is an artificially simple case, unrepresentative of cases such as explaining someone's purchasing theater tickets in anticipation of surprising arriving guests. In the latter case, of human behavior, there is little expectation of our being able to predict the purchase nor can we deduce the description of the event from antecedent conditions and known scientific laws. Wittgenstein (1889-1951), although himself having once been a formalist, denigrated the formalists' approach when he wrote in his posthumous Philosophical Investigations: {page 37} It would be tempting to ask, "Well, who is right, the formalists or their critics? Which is the correct way to go about doing a philosophical analysis?" If only such questions had straightforward answers. But they do not. I can see no way at all to offer an answer without begging* the very question being posed. Formalists will answer in one fashion, non-formalists in another. But who, or where, is the neutral, objective referee who can adjudicate the debate? So far as I can tell, at this point, when we have begun to ask questions about how philosophy is to be done, there can be no definitive or authoritative answers. As I said earlier, each of you must sample philosophical approaches to find one suitable for yourself. At some point argumentation comes to an end and it becomes time simply to choose. When I was much younger, I did not at all have this attitude toward philosophy. I was convinced that there must be good arguments for the resolution of any philosophical question. My teachers seemed so sure of their own philosophical bearings. They never seemed to experience, let alone confide in us students, any qualms or misgivings concerning what they so confidently professed. And for a while I, too, shared something of what I took to be their attitude: that one can achieve knowledge and certainty in philosophy, that with effort and conscientiousness one could aspire to truth in philosophy just as one could in science. I believed that there were objective standards in philosophy just as in science and that we philosophers could, if we were willing to do the work, achieve consensus in our philosophy. Thirty-five years later that youthful optimism has completely evaporated. I have unburdened myself of that comfortable delusion. Indeed, I have gone one step further. Unlike my own teachers, I often and emphatically explain my own views about philosophy to my students, telling them quite explicitly that although I am prepared to present my views with as much verve as I can, I do not want them to mistake my enthusiasm for a conviction of certainty. I am certain of {page 38} almost nothing I teach my students. (And likewise for the bulk of this book.) My lack of certainty, however, has not dulled my interest. Certainty has given way to what I regard as a more mature understanding of human theorizing. We do the best we can, but in the end we can prove almost nothing of what we believe, say, or write.9 Why, exactly, this is so, or, more precisely, why exactly I believe this, I will try to explain in the following two chapters. There I will argue that our theorizing is underdetermined by the evidence we offer in support of our theories. And I will argue that this indeterminacy is not just a feature of our philosophizing, but permeates our attempts to do science as well. But this is to anticipate.
Some contemporary anthropologists and psychologists have taken to describing Homo sapiens as the storytelling species, and by this they mean that we human beings are constantly constructing stories (hypotheses/theories) in order to make sense of both the usual and the unusual. These stories range from the myths of primitive societies to the highly sophisticated theories of quantum mechanics and astrophysics, from the commonplace ("there are parallel black marks on the pavement; probably a car skidded") to the highly speculative ("there is intelligent life elsewhere in this galaxy") and to the outrightly metaphysical ("there is in each of us an immortal soul"). But whether this metaphysical view – that there exists within us a deep motivation to try to construct ever more and ever better explanations – ever achieves wide acceptance, there is one thing that must be said of it: it has an endearing kind of selfillustration, for it would itself appear to spring from the very source it purports to describe. |