|
Beyond Experience: Metaphysical Theories and Philosophical
Constraints, Second Edition, Copyright © Norman Swartz, 2001.
Available for downloading, free of charge, at http://www.sfu.ca/~swartz/beyond_experience. {page 145} CHAPTER EIGHT Space and Time In our conversation, no word is more familiarly used or more easily recognized than "time". We certainly understand what is meant by the word both when we use it ourselves and when we hear it used by others.Augustine's dilemma is one all of us have experienced frequently in our lives, not only about time, but space, morality, justice, education, art, etc. We are perfectly capable of using these concepts in our ordinary affairs; but we seem unable to give an explication, or – better – a theoretical reconstruction, of these concepts. All of us understand the concept of time well enough to schedule meetings, to set alarm clocks, to time a cake's baking, and the like. But if asked "What is time?", most persons – like Augustine – would not know how to answer. 8.1 Is it possible to explain what space and time are? Time and again when I was a student in public school, my teachers solemnly insisted: "In spite of everything we know about electricity, we do not know what electricity is." This verdict about electricity can be found, too, in many books of the period.  To use Popper's phrase
(he
{page 146}
was speaking of objections to Einstein's relativity theories;
[159], 34), this was – in the end – just a piece of
"popular nonsense". To use Popper's phrase
(he
{page 146}
was speaking of objections to Einstein's relativity theories;
[159], 34), this was – in the end – just a piece of
"popular nonsense".
What made that slogan nonsense stemmed from a certain presupposition that prompted it. When asked to explain what it meant to say "We do not know what electricity is", my teachers would often reply with something of the sort, "We know that electrical phenomena arise out of the movement of charged particles, and we know many of the physical laws involved, but however much knowledge we gain of this sort, it will never tell us what electricity is." I have no doubt that my teachers were well-intentioned, that they honestly believed that this was a legitimate thing to say and to impart to their students. But in the end, it is nonsense nonetheless. It is nonsense because as a general principle it would deny that we know of anything at all what it is. There is nothing special in this regard about electricity. What my teachers alleged to be a peculiar problem with electricity could just as well have been said about glass, the wind, your nose, profit, or freedom. And quite contrary to their argument, we know what things are precisely by knowing what their makeup is, what sorts of physical laws describe their behavior, how they typically act, and how we make use of them. We know, for example, a great deal about the wind. We understand that the wind is not the exhalation of a god but is movement within the atmosphere in which we live. We have learned, too, that air is made up of a mixture of various gases, that air moves because of differential heating (due to the Sun's heat, ocean currents, concentrated burning of fossil fuels, etc.) and because of the Coriolis force (due to the rotation of the Earth), and that air may move in laminar or turbulent ways. And we have learned, over a period of centuries by trial and error and more recently with the greater efficiency conferred by having mathematical theories of gas dynamics, to harness the wind (in windmills, for example). Once we know these sorts of things, even if our knowledge is incomplete, even if, for example, we cannot predict or explain the behavior of the wind as precisely as we might like, we know what the wind is. And the same may be said for electricity: once we know the atomic nature of electrical phenomena, have discovered a great many of the physical laws of those phenomena, have harnessed electricity in our generators, machines, radios, computers, and the like, we may perfectly reasonably say, "For the most {page 147} part, we know what electricity is." Of course we cannot sum up this extensive knowledge in a brief paragraph. A good understanding of electricity comes about only after several weeks or months of study. But it is something attainable with effort. It is certainly nothing unknowable in principle. The moral should also be applied for space and for time. Just as in the case of electricity, many persons have, like Augustine, convinced themselves that there is something deeply mysterious about space and time and that space and time are so inscrutable as to be unknowable. "In spite of everything we know about space and time, we really do not know what space and time are", I think many persons are inclined to think to themselves. Certainly there are problems about space and time, but the pessimistic belief that space and time are somehow so enigmatic as to be fundamentally unknowable strikes me as a piece of popular nonsense which ought to be excised just like the nonsense about electricity. What does coming to know what space and time are consist in? The answer, I suggest, is perfectly straightforward: it consists, simply, in our having an account which is, first of all, free of internal inconsistency, and, secondly, robust enough both to make sense of our ordinary uses of these concepts and to allow us to do physics. Common, everyday notions of space and time, as Augustine noted seventeen centuries ago, are in quite good enough shape for ordinary affairs. But they are not in particularly good shape for sophisticated thinking about the universe writ large. Buber, we have earlier seen, had tried to imagine an edge of space and a beginning and end to time and found that he was unable to imagine that there could be such things and (unfortunately for him) was unable to imagine that there could not be such things. Recall (from p. 10 above): "A necessity I could not understand swept over me: I had to try again and again to imagine the edge of space, or its edgelessness, time with a beginning and an end or a time without beginning or end, and both were equally impossible, equally hopeless – yet there seemed to be only the choice between the one or the other absurdity" ([37], In this passage, Buber, writing years later, correctly – but unwittingly – diagnoses the source of the problem: the very ideas at play are 'absurd'. But he never clearly plumbed the absurdity, either as a teenager or as a mature philosopher relating his youthful experience. The source of Buber's difficulty is an untenable concept of space. It is deeply and irremediably flawed, for it leads, as we see explicitly in Buber's narrative, to incoherence. In Kant's terminology, this particular concept of space was beset by 'antinomies'. In modern terminology we would deem it 'paradoxical'. {page 148} Leibniz, in contrast, had a significantly different concept of space. In spite of certain difficulties1 in his theory of space, I am tempted to say that in the fundamental insight which informed his theory, Leibniz 'got it right'. However, if I were to put my praise in just that way, I would undercut what I said earlier about philosophical reconstructions, viz. that they cannot be judged to be true or false. So, forgoing the claim that Leibniz 'got it right', I am inclined to say that Leibniz's account is vastly superior to the common view and, with some repairs, can be made to work reasonably well. (Hereafter, I will refer to the theory being offered below as the "neo-Leibnizian" theory. The qualification "neo" connotes that what follows adopts the core of Leibniz's original theory, but is not to be thought to preserve the whole of that historical theory.) Let me state the essential element in the neo-Leibnizian theory of space in an initially provocative manner, using a form of words only slightly different from Leibniz's own: Space does not exist.
The neo-Leibnizian theory can equally be characterized as being the 'negative' theory of space. It argues, in effect, that there is nothing more to the concept of space than that places are dependent on the existence of physical objects.2 Take away those objects and there are no 'places'. In imagination annihilate all the matter of the universe. Having done so, in no intelligible sense can you then go on to say: "This is the place where the Andromeda galaxy used to be." Without physical things, there are no places. To say of a world devoid of physical objects that one place might be distinguished from another would be of the same order of nonsense as to say that someone might vacate a room and leave her lap behind. Just as a lap is a spatial feature of one physical object, places are spatial features of two (or more) physical objects. In the absence of physical objects, there are no places. Still less is there a 'physical space' which might be thought to be the conglomeration of all places.
But having now stated the thesis – that space does not exist, that there are only things and their places – in a deliberately provocative way, let me try now both to explain what I mean by this and to defend (what must surely appear at the outset to be) an outrageous claim. {page 149} 8.2 A neo-Leibnizian theory of space It is a truth of logic that any class of things can be divided, without remainder, into two mutually exclusive subclasses. Roses, for example, may be divided into all those that are red and all those that are not red. Mammals, for example, may be divided into those that are marsupials and those that are not. And similarly for theories of space, which may be divided into those theories which posit space as a subtle (ethereal) kind of 'stuff' permeating the universe and those theories which do not so regard space. Isaac Newton, like most persons, subscribed to a theory of the first kind, although Newton's theory, as we would expect, was considerably more robust than most persons'. Motivated in part by a Cartesian* theory of perception and in part by certain theological beliefs, he posited that space was, in his words, 'the sensorium of God', a kind of 'sense organ' by which God was able immediately to know the place (whereabouts) of anything in the universe. We will not concern ourselves with these latter sorts of subsidiary features of Newton's theory. What is essential in his theory was that it was one of the kind which regarded space as a 'container' of the physical objects in the universe. Most persons, I am quite sure, subscribe to a 'container' theory of space. When they say such a thing as "There are many galaxies scattered about in space", they will often imagine a picture, just on a grander scale, similar to that imagined when they say, for example, "The Eiffel Tower is located in Paris." Just as the Eiffel Tower and Paris may each be regarded as a kind of spatial object (although of course the latter is a rather large spatial object, occupying some 106 square kilometers), the common view would have it that galaxies, too, are physical objects (very big ones) and that they are located in space, viz. a yet larger container (a kind of 'super-Paris' as it were) which is, nonetheless, a 'somewhat physical' sort of thing. The reasoning is by analogy: the Eiffel Tower (a physical thing having spatial properties) is in Paris (also a physical thing having spatial properties), and thus galaxies (physical things having physical properties), being in space, must be in a thing (i.e. space) which in its turn is a physical thing having spatial properties. This 'container' model of space is unquestionably the one presupposed by Buber. He conceived of space as a kind of stuff of which it was appropriate (meaningful) to speculate where its edge might lie. For containers, whether they be something as small as jam jars or as large as Paris, have outer bounds: there clearly are places which lie on the 'inside' (i.e. are within) and there are other places which lie on the {page 150} 'outside' (i.e. are without). But, as we have seen (p. 10 above), Buber nearly went insane trying to reconcile himself to operating with this model of space. Leibniz strongly attacked the 'container' model of space. His particular challenge was to Newton's particular version, but it need not be regarded as so restricted. His objections, and his alternative theory, can be read as applying to any version of the 'container' theory. §2.And in the following paragraph Leibniz talks of the "chimerical [fictitious] supposition of the reality of space in itself" (26). What all of this comes down to is Leibniz's arguing that space does not exist; that there are physical objects which, as we say, are 'in space', but space does not exist as a distinct further kind of thing which 'contains' these objects. In reading Leibniz's characterization of Newton's theory as one of an "absolute" space, and his own as one of a "relative" space, one must recall that these terms did not mean quite the same to seventeenth-century writers as they have come to mean in the period since Einstein proposed his theories of the relativity of space. When Einstein wrote, early in the twentieth century, that space is "relative", he was advancing a thesis which clearly presupposed the neo-Leibnizian concept of space, but which advanced – at the same time – claims about the universe, and in particular about mass, energy, gravity, and the transmission of light, which were never dreamed of by Leibniz. It is no part of my concern here to review Einstein's theories. What I am attempting to do is to propose a theory of space and time which is consistent with modern physical theory and which {page 151} provides a suitable base on which to erect current theories in physics. I will content myself, that is, with arguing against a common, but woefully confused concept of space and time, a concept totally inappropriate for the doing of modern physics. When Leibniz contrasts his own theory with that of Newton, saying that Newton hypothesizes that space is 'absolute' and that he, instead, hypothesizes that space is 'relative', we must understand that Leibniz is not saying that each of them is arguing that space is a kind of stuff and that they are arguing about whether it is one sort of stuff or another. Quite the contrary, in his saying that Newton subscribes to a theory of absolute space, Leibniz is arguing that Newton believes that space is a kind of stuff. In contrast, when he himself argues that space is relative, Leibniz is arguing that space is nonexistent, in his own words, that the reality of space is "chimerical". In the Newtonian world-view, space and its contents are two different sorts of things; each exists. And although physical things could not exist except by being (at some determinate point or other) in space, space could exist even if it were devoid (empty) of all physical things whatsoever. This view, as I have said, is more or less the commonly held view of space. Leibniz's view is far more economical, but distinctly at variance with common, popular views. In Leibniz's view, physical objects do not 'inhabit' space. Physical objects exist; some touch one another; others are separated by various distances from one another; but there is no further kind of 'stuff' (space) filling up the places where there are no physical objects. There is, of course, one immediate benefit from adopting the neo-Leibnizian theory: it solves Buber's problem at a stroke. If space does not exist, then it neither has nor lacks an edge. If space does not exist, then there is no place which lies 'within' space and some other point which lies 'without'.3
Many persons find this particular manner of solving philosophical puzzles deeply disturbing and find themselves resisting the proposal. {page 152} To them it seems something of a cheat to attempt to solve a puzzle by undercutting its presuppositions. Thus, for example, some persons have balked at Russell's solution to the famous Barber paradox. Russell described a male, adult barber, who himself had whiskers, who shaved all and only those persons in his village who did not shave themselves ([179], 261). The question arises: Who shaves the barber? Whether one answers that he is unshaved, that he shaves himself, or that someone else shaves him, the answer immediately contradicts one of the explicit claims made in the description of the barber. Russell's solution – and indeed the only solution possible to the puzzle – is to recognize that the very description given of the barber is internally incoherent, i.e. it is logically impossible that there should be such a barber. The puzzle can be solved, in effect, only by 'backing up', as it were, and challenging one of the presuppositions of the very problem itself. One 'solves' such a problem, not by answering it, but by rejecting the problem, by showing that it harbors an untenable presupposition.4
Buber could not solve his problem. That either answer led immediately, in Buber's own words, to "absurdity" is evidence not of the profundity of the problem itself, not of the need for ingenious solutions, but of something fundamentally incoherent in the very problem itself. And what that incoherence consisted in, I suggest, is the popularly held, but ultimately untenable, view that space is a kind of 'stuff' of which it is appropriate to imagine that it has a boundary and of which it is appropriate to ask what lies within it and what lies outside it. This 'absolute' (or 'container') notion of space cannot be freed of incoherence. There is an altogether different sort of argument which may also be brought to bear against the concept of space as being a kind of 'stuff', an argument from English grammar. Consider the two English sentences, (S1) There is water between the chair and the wall. and (S2) There is space between the chair and the wall. From a point of view of English grammar, these two sentences are identical. From a grammatical point of view, they match word for {page 153} word, phrase for phrase. But in spite of that, there is something profoundly different about these two sentences. The concepts water and space which occur in them behave unexpectedly differently from a logical point of view. The remarkable dissimilarity is revealed when we try to paraphrase these two sentences. For the latter can be given a paraphrase which is anything but possible for the former. (S2) may be paraphrased this way: (S2') There is nothing between the chair and the wall, and the chair is not touching the wall. In this paraphrase, only two sorts of 'things' (or stuff) are referred to: the chair and the wall. Talk of space has dropped out altogether. No such paraphrase is possible for (S1). For in (S1), there really are three sorts of things involved: chairs, water, and walls. But space is not a sort of thing, and this is revealed by the remarkable paraphrase possible for (S2). Two points need to be made about this maneuver. First, and foremost, is the need to address the objection that the paraphrase does not genuinely eliminate talk of space as a kind of stuff, it merely substitutes a synonym, viz. "nothing", in its place. For some persons, in reflecting on the paraphrase (S2'), will believe that they detect in it a reference to three kinds of things: chairs, walls, and nothingness. Indeed, some persons quite explicitly regard "empty space" and "nothingness" as We have, it seems, offered a solution to one philosophical problem, only to have it replaced by another. Is "nothing", when used in a sentence such as "There is nothing between the chair and the wall", to be regarded as referring to a thing in the way in which "the chair" and "the wall" refer to things? What role does "nothing" play in such a sentence? The debate over the question what, if anything, "nothing" denotes has a long and checkered history in philosophy.5 Philosophers are split into two camps: those that regard "nothing" as denoting something (viz. the nothingness) and those that regard "nothing" as playing a non-denoting role in our sentences.
Lewis Carroll (1832-98), the author of Through the Looking-Glass (who was by profession a mathematician and by avocation a philosopher), {page 154} spoofs the view which would make of "nothing" (and "nobody") the name of something (or someone).6
"Who did you pass on the road?" the King went on, holding out his hand to the Messenger for some more hay. "Nobody," said the Messenger. "Quite right," said the King: "this young lady saw him too. So of course Nobody walks slower than you." "I do my best," the Messenger said in a sullen tone. "I'm sure nobody walks much faster than I do!" "He can't do that," said the King, "or else he'd have been here first." ([46], 196)Many twentieth-century philosophers, especially those among the Continental schools and the Existential schools, have written of Nothingness, treating it – as the King regards "Nobody" in Carroll's fable – as referring to some actually existent thing. They have talked of the fear of Nothingness and of the anxiety caused by the prospects of Nothingness. Some of these philosophers identify Nothingness with death; and others with 'the void'. But other philosophers will have nothing (!) of that kind of theorizing. These latter philosophers (myself among them) regard "nothing" as playing a different kind of role in our sentences. "Nothing", according to this theory, is just one among several so-called quantifiers, words which, in effect, serve to indicate the size of the classes one is talking about. Thus, for example, we might say, "Everything troubles me today", or "Practically everything is troubling me today", or "Something is troubling me today", or – finally – "There is nothing troubling me today". What this latter sentence says, I would urge, is that there is not anything that is troubling me, i.e. that I am free of troubles. "There is nothing troubling me today" ought not, I suggest, be thought to be saying that I am being troubled and what is doing that troubling is Nothing.7
{page 155} Along perfectly similar lines, when we offer a paraphrase of "There is space between the chair and the wall" which reads "There is nothing between the chair and the wall and the chair is not touching the wall", the latter ought to be understood as saying "There is no (third) thing between the chair and the wall" rather than as saying "There is some third thing between the chair and the wall, namely, Nothing." If "Nothing" named a kind of thing in the world, then – by parallel reasoning, it seems to me – so too would "something", "practically everything", "hardly anything", "most", and "a few", etc. None of these, I suggest, names anything in the world. No more so than does "it" in "It is raining" or "there" in "There is a car in the driveway." If one identifies space with The Nothing, then one immediately invites back Buber's conundrum, only it now reads: "Where does the Nothingness leave off, and what is on the other side?" The second concern arising over the maneuver of 'paraphrasing-away', as it were, the reference to space as a kind of thing does not so much question the results of applying that technique, but challenges the very technique itself. Some persons are deeply suspicious and troubled over the technique of solving philosophical problems by grammatical or linguistic means. Even cheerfully admitting the correctness of the paraphrase, some persons will resist seeing it as a genuine solution to the original problem. The objection they make is to the alleged relevance of the paraphrase to solving the problem. Again, just as in the case of Russell's proposed solution of the Barber paradox, persons will have differing attitudes about the philosophical methodology involved. Persons come to philosophy with different expectations. What one person sees as a perfectly cogent solution to a {page 156} problem, another person may fail to regard as even being relevant. For some persons, the demonstration that "space" has a quite different 'logical grammar' from ordinary substantive terms, such as "water", "wall", and "chair", does nothing to address the problem of sorting out the concept of space. Linguistic maneuvers, of the sort we have just gone through paraphrasing away "space" in (S2), are regarded as mere 'word-chopping' or 'hairsplitting', but not as grappling with the deep conceptual problems afoot. Other persons, in being presented with precisely the same paraphrase and the accompanying discussion of how "space" and "nothing" do not behave grammatically like (incontrovertible) substantive terms such as "water", "wall", and the like, experience something of a 'Eureka'-flash, and come to regard problems like Buber's as having their source in thinking of space as if it were an (ethereal) kind of thing. In my own classroom, I often see the different attitudes persons have toward these methods. On encountering the method of paraphrase and the claim that it can sometimes reveal important distinctions among our concepts, some of my students will embrace it with zeal and regard it as revelatory while others of them will reject it with open contempt. Who is right? How does one adjudicate when fundamental conceptions about the very practice itself of philosophy are at stake? How does one argue in support of, or against, the method of paraphrasing as a means of solving some philosophical problems? Certainly great numbers of modern philosophers use such techniques: if not every day, then at least on some occasions. One can hardly pick up a current philosophical journal without finding within it some article in which the writer has utilized it or a kindred technique. But for the person unfamiliar with, or unused to, such techniques, to whom such techniques seem linguistic sleights of hand, who initially regards them as being some sort of cheat, how is one to recommend and justify the adoption of such a technique? There can, of course, be no definitive answer. There can be no answer which is ultimately assured of winning converts to a methodology which some persons view with suspicion or disfavor. It is no more possible to find a way to convince one's opponents of the rightness or utility of a philosophical methodology than it is to find a way to convince one's opponents of the profit of looking at the world through the eyes of a new scientific theory or adopting a new technology. In spite of the commonly held view that there is some one canonical 'scientific method', its existence is, when all is said and done, mythical. Similarly, {page 157} there is nothing that can be called 'the' philosophical method, either. Philosophers are bound to disagree among themselves about philosophical methods, just as scientists are bound to disagree over scientific methods. There is no argument in support of the method of paraphrasing which will be convincing to all doubters. One can do no more than apply that method to various cases, display the results, and invite one's readers to decide for themselves whether they regard the method and its results as acceptable. My own attitude has been to adopt the method as one tool among several to be used in struggling to explicate our concepts. I am happy to utilize it in the present case because its results cohere with the results of other approaches and because its results offer a solution to Buber's problem and because the method offers a concept of space suitable for erecting modern physical theories. This is not to say that I believe that the method of paraphrase is the touchstone for doing philosophy. Quite the contrary, I believe that in some instances it has been used in a jawbone fashion, for example in the analysis of the concept of causation where it has been applied – in the hands of some philosophers – to too few examples, and thus been used to advance an overly restricted explication of "cause". In short, I do not rest my case, of arguing that space is nonexistent, simply on the basis of a paraphrase of (S2). I build the argument on that paraphrase, to be sure, but on much else besides, e.g. that such an explication solves Buber's problem and that such an explication coheres with modern physical theories whereas a 'container' notion of space does not. 8.3 Objections and replies to the neo-Leibnizian theory It has been my own experience that most persons relish a lavish ontology*. By this I mean that most persons prefer a conceptual scheme in which there figure a great number of kinds of things. The term "things" here is meant in a very broad, inclusive sense. On this interpretation, "things" will include, of course, the most familiar things of all, namely physical objects, but will include as well all sorts of nonphysical things, e.g. minds (if indeed they are nonphysical), supernatural beings, numbers, classes, colors, pains, mathematical theorems, places, and events. In short, "things" is being used here as a general name for any sort of thing (!) whatsoever that can be named or described. Most persons, it seems to me, are willing to prune their ontologies {page 158} only with reluctance. Few persons cheerfully or readily are willing to discard items from their stock-in-trade ontology. Every philosopher who has ever argued that some item or other in the popularly held ontology is expendable insofar as it is mythical or incoherent has, I am sure, met with resistance from persons arguing that the suggestion is a patent offense against common sense. There is much to be said for the commonsense view of the world. Foremost is the fact that it works extremely well. One tampers with it only gingerly and always at some risk of damaging it. But commonsensical views of the world are not perfect and are not immune to change and improvement. One can sometimes improve on common sense, but one must take care in trying to do so. For a good deal of suggested repair – e.g. that disease is a myth – is downright dangerous. The neo-Leibnizian theory I have described above, the theory that space does not exist, i.e. that there is no such thing as space, is guaranteed to elicit from many persons the objection that it does so much violence to common sense that it is simply fantastic. The concept of space as being a kind of thing is so pervasive in our commonsense view of the world that any suggestion that space does not really exist is regarded as a philosopher's fancy not to be seriously credited. Let me try, somewhat further, to undo this sort of resistance. Let me try both to show how the theory works, and how it succeeds in preserving what is valuable in common sense and how it discards what is problematic in the commonsensical view. Objection 1: Lord Kelvin once extolled the virtues of measurement this way: "
Reply to Objection 1: The theory of space being proposed here must not be thought to deny the possibility of our performing such measurements. Any theory which said that it is impossible to measure the distance between chairs and walls would be at such gross variance with simple physical facts as to be worthy of rejection immediately. The neo-Leibnizian theory, obviously, cannot deny such 'hard facts' if it is to be seriously entertained. And indeed it does not. Quite the contrary, Leibniz implicitly allows that such measurements are possible ([5], Fifth paper, §54, 75). Certainly it is possible to measure the distances between many physical objects. For ordinary-sized physical things, close at hand, we can use calipers and meter sticks; for greater distances, surveyors' transit theodolites; and for still greater distances, radar, parallax measurements, and Doppler red-shift measurements. All of this simply must be admitted, and indeed all of it is left perfectly intact in the neo-Leibnizian theory. Even more to the point, this theory makes the picture of physical objects standing in various spatial relationships to one another its fundamental notion. According to the neo-Leibnizian theory, it is precisely physical objects and their spatial relationships which are real. What {page 160} is denied to be real is some sort of pervasive 'stuff' (i.e. space) of which these relations are somehow to be thought of as properties. In this neo-Leibnizian theory, from the point of view of physics, what exists are physical bodies, persisting through time, some very small (including the molecules of the gaseous mixture air), others immense, some touching one another, others at various distances, some at relative rest, i.e. not moving with respect to some object conventionally chosen as the 'fixed point', and yet others in motion with respect to that 'fixed point'. But that's it. There is no further ethereal soup (space) in which all these objects 'float', as it were, like fish in the sea. But if there is no ethereal 'stuff' between objects, then Buber's peculiar views of the world cannot arise. What we have in this theory is what is worth preserving, viz. physical objects of various sizes moving about with respect to one another. What falls away is precisely, and only, that part of the picture which was problematic: the idea that space was a further kind of 'thing' of which it was appropriate to imagine that it, too, had an 'inside' and an 'outside'. Objection 2: It is not simply that we are able to measure the distance between non-contiguous objects. It goes well beyond that. Physicists, astronomers, cosmologists, and geometers attribute geometrical properties to space, e.g. they are wont to talk of space being "curved" and of space having "three dimensions". Surely only an existent thing can have such physical properties. If there is curvature, then there must exist something to be curved; if there are three dimensions, then there must exist something to be three-dimensional. Reply to Objection 2: The definition of "curvature", as a mathematically calculable measure, was invented by Gauss (1777-1855) in two papers of 1825 and 1827 on the geometry of two-dimensional10 surfaces ([76], 15, 97). The Gaussian measure of the curvature at any {page 161} point is the reciprocal* of the products of the greatest and least radii of curvature at that point. For example, consider the curvature at a point on the 'equator' of a perfect sphere. The surface curves equally in all directions, e.g. along the equator itself and along the line of longitude through that point; i.e. both these circles have the same radius. Let us call that radius "R". The measure of the curvature, then, according to the Gaussian formula would be
Imagine now the sphere growing to infinite size: the surface is (effectively) flat, and the radius is infinite (i.e.  ). The Gaussian
formula tells us that the curvature is ). The Gaussian
formula tells us that the curvature is
 x x  ), ),Thirdly, imagine a doughnut-shaped surface, or as mathematicians call it, a torus (pl. tori). Imagine it to be oriented as if lying on a tabletop. (See figure 8.1, p. 162) Choose a point on the inner surface, i.e. on the perimeter of the hole in the middle. (In figure 8.1, see the left-hand side of the lower diagram.) There are two circles here, at right angles: a horizontal circle (whose radius is labeled "R") comprising that inner perimeter; and a vertical circle (whose radius is labeled "r"), that of the cross-section through the dough of the pastry. (If you prefer, imagine two interlocked key rings, touching at right angles.) What makes this case importantly different from the preceding two is that the two radii of curvature are in opposite directions. If one is assigned a positive value, the other must be assigned a negative value. Assume one is +r and the other is –R. Then the Gaussian formula gives a negative value for the curvature, i.e.  and
r,
point in the same direction, and hence the curvature is
positive.11) and
r,
point in the same direction, and hence the curvature is
positive.11)
As Gauss originally introduced the concept, to apply to features of {page 162} 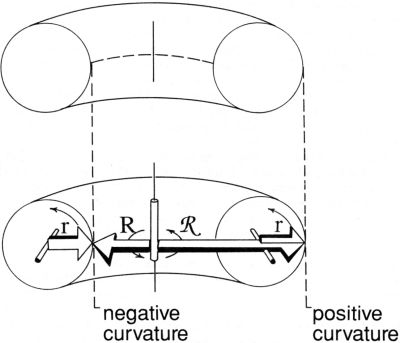
two-dimensional surfaces, curvature is readily grasped. But it was not long before the concept was extended in 1854, by Riemann (1826-66), to apply, not to two-dimensional surfaces, but to three-dimensional space ([173]). For a mathematician, a 'space' may be of any number of dimensions. Indeed, a 'space' need not refer to anything physical whatever: it is just a measure of the number of 'dimensions' needed to specify the 'location' of something of interest. For example, Helmholtz cites the case of the three-dimensional 'space' of colors: any given color may be located in the (finite) three-dimensional space of red, green, and blue, by specifying for each of these 'dimensions' (primary colors) what percentage occurs in the given color. (He omits intensity; had he included that parameter, he would have needed a four-dimensional 'space' {page 163} which was finite in three of its dimensions, and infinite in the fourth.) If someone offered a theory of intelligence, for example, in which there were five independent parameters to be measured – e.g. verbal skills, mathematical skills, physical skills, creative skills, and social skills – then one would have to posit a 'space' of these five dimensions in which to locate any given person. From the mathematical point of view, there is utterly no difference between the 'spaces' of geometry, of color spectra, and of intelligence. All of these, and countless other 'manifolds', are called "spaces". Even philosophers have adopted the concept and sometimes talk (perhaps a bit pretentiously) of such esoterica as "logical" space. When Riemann extended Gauss's original concept of the curvature of two-dimensional surfaces to a three-dimensional space, we must understand that he was proceeding by mathematical analogy. He was, in effect, arguing that certain features of three-dimensional geometry (and by extension, four-, five-, six-, indeed any n-dimensional geometry) would be extensions of features of two-dimensional geometry. In any analogy, certain features are preserved and others discarded. And in extending Gauss's original notion, devised for two-dimensional geometry, to three-, four-, or higher-dimensional geometries, we must take care to understand exactly what may be carried over and what is to be discarded. Riemann discovered that in a 'positively curved' space, many of the familiar theorems of Euclidean geometry do not hold. For example, in such a space, there are no parallel lines and the sum of the angles of triangles always exceeds 180°. But what, exactly, is one to make of this notion of a 'positively curved' space? The intellectual puzzle arises because of the difficulty we have in trying to extend the familiar notions of curvature which were introduced, in the first instance, to apply to two-dimensional surfaces: of the sphere, of the torus, etc. To be sure, the sphere and the torus are three-dimensional objects; but their surfaces are two-dimensional 'spaces'. We can intuitively grasp the sense of "curvature" operative in these familiar cases because we can visualize that the curved surfaces are the two-dimensional surfaces of a three-dimensional figure. But when we are then told that our own physical space is (or might be) curved, and we try by analogy to visualize it as being the surface of some four-dimensional solid, our imaginations fail us. The analogy becomes more hindrance than help. Mathematicians are practiced enough to know how to handle the analogy correctly. Mathematicians, that is, know how to abstract the essential mathematical features from such examples – the plane, the {page 164} sphere, the torus, etc. Non-mathematicians, however, are done a disservice by these models, for they are not practiced in focusing in on just the relevant mathematical features at play, and are far too likely, virtually inevitably likely, to be distracted by the robust reality of the physical objects (the Earth, the hunting horn) which 'sport' these curved surfaces. What the mathematician wants to focus on in these models are the surfaces themselves, divorced from the things of which they happen to be the surfaces, i.e. the mathematician is concerned solely with the mathematical, not the physical, properties of these surfaces. But all of this is usually lost in most popular presentations of modern geometry. Already in the nineteenth century, Hermann Helmholtz recognized non-mathematicians' inability to handle the concept of curvature in the manner of physicists and mathematicians, i.e. he recognized that non-mathematicians tried to conceive of the curvature which was said to characterize physical space after the model of curvature which was familiar in the case of the two-dimensional surfaces of three-dimensional objects. Helmholtz advises that one abandon any attempt to conceive of curvature in that manner. Instead we should conceive of curvature as the result of a certain kind of calculation we perform on quantities we measure with our instruments. All known space-relations are measurable, that is, they may be brought to determination of magnitudes (lines, angles, surfaces, volumes). Problems in geometry can therefore be solved, by finding methods of calculation for arriving at unknown magnitudes from known ones.Helmholtz, like Riemann himself, regards this 'new talk' of curvature, not as describing perceivable, or even imaginable, properties of space, but rather as a result to be obtained by mathematical calculation on measured quantities. In modern science, too, many writers repeat the advice, cautioning readers explicitly about the potentially misleading use of the word "curved". The astronomer Dennis Sciama, for example, writes that it is misleading to talk of non-Euclidean space as "curved". But his point is perfectly general, and does not apply only to non-Euclidean space, for it is, in a way, just as misleading to describe Euclidean space as "flat". I will bracket certain phrases in quoting him, so as to make his point more general. In this instance, bracketing indicates not my insertions, but rather my suggested deletions from the original: "We can easily understand what it means to say that a two-dimensional surface is curved, because we can see this surface lying in three-dimensional [Euclidean] space, and the meaning of the word 'curvature' is quite obvious. But when this same name 'curvature' is also given to a three-dimensional [non-Euclidean] space (footnote: let alone four-dimensional space-time!) it becomes rather misleading.
Talk of space itself being curved has become commonplace within physics. But one must beware not to interpret such talk too literally, or at least not with the common meanings we assign to the word "curvature". We should no more want to regard the physicist's use of the term "curvature" as being akin to the ordinary use than we should want to regard the physicist's use of the word "field" as being akin to the farmer's. In suggesting that we should deliberately and consciously try to resist the temptation to conceive of space as a kind of subtle, tenuous, ethereal, or subliminal kind of 'stuff', the sort of thing which begs us to try to imagine where its boundaries might be or what its curvature or geometry might be, I am not suggesting that we reform our language so as to purge it of the word "space" or that we cease altogether to talk of space. To try to avoid talking of space strikes me as futile and as foolhardy an enterprise as some have attempted with certain other terms. History provides us with the spectacle of a number of linguistic cultists who have trained themselves to speak without ever uttering words which they regarded as 'corrupt' – not barbarisms like "priorize", "irregardless" and "de-hire", but perfectly ordinary nuts-and-bolts words such as "but" or "not" and even (incredibly) "is".13 (I have had students, bamboozled by bizarre linguistic theories, try to explain to me that every time one uses the word "but" in describing the behavior of another person, one has insulted that person.14)
Some proposals to reform language are grounded in good reasons; some are not. Certain proposals – e.g. to use nonsexist pronouns and {page 167} nonsexist descriptive terms or to eliminate offensive racist and ethnic labels – have powerful ethical warrant. However, there are no similarly good reasons – either on ethical or on any other grounds – for eliminating such words as "is", "but", and "space". These latter sorts of terms, or equivalents, are enormously useful, being well-suited for most contexts. It would be pointless and counterproductive to abstain from using the word "space". All of us, myself included, will surely continue to say such perfectly intelligible and correct things as "There is not enough space on the shelf for this book" or "There is too much space in the garden to conceal with a single rosebush." My suggestion is only that, even though we use the word "space" often and with propriety, we not allow ourselves to think that the term designates some sort of tenuous 'stuff'. When we find ourselves lapsing into the kinds of speculations which so befuddled Buber, and perhaps ourselves earlier, it is at that point that we should remind ourselves that "space" does not function in our language like "water", that any sentence containing the word "space" can be paraphrased so that talk of "space" drops out. ("There's not enough space on the shelf for this book" might become, for example, "If all the objects on the shelf were to be shoved to the left end of the shelf, then the distance at the right end, between the last object and the right edge of the shelf, would be less than the width of this book.") George Berkeley (1685-1753), perhaps paraphrasing Francis Bacon, wrote: " Objection 3: The idea that space exists derives not just from common sense, or even, for that matter, from physics, but from perception. Space is not a theoretical posit, or hypothetical entity, in the way in which the 'collective unconscious' might be thought to be. Quite the {page 168} contrary, space is every bit as perceivable as are physical objects. For I do not see only physical objects, I can also see the space between them. On clear moonless nights, I can look up at the sky and see the very blackness of space itself. In short, I can see space. Since I can see space, and since I am experiencing neither an illusion nor a delusion, space must, then, exist. Reply to Objection 3: It is perfectly clear what the reply must be to this last objection. Someone holding to a neo-Leibnizian theory of space, who thereby wishes to deny the reality of space, must counterargue that space is not visible. But can one reasonably do this? Is not space visible in just the same sort of way, for example, that my hand is visible when held up before my eyes in a well-lighted room? There are, I think, two different sorts of cases where one might think one is perceiving space itself, and we would do well to examine both of them. The first sort of case involves ordinary, daylight perception, the kind you and I regularly experience as we look about ourselves in well-lighted places. What do we see? Typically, all sorts of physical objects – tables, chairs, pictures on the walls, carpets, human beings, etc. (if we are indoors); buildings, trees, roads, flowers, clouds, human beings, etc. (if we are outdoors) – lying at different distances from our vantage point. These many things are scattered about in different places, and often there are few if any other things occupying the places between them. About this we can all agree, and up to this point we give identical reports. But is there something more to be seen? Is there, in addition to the sorts of things just mentioned, space as well? Do we see space between the objects? To be sure, we say such things as "I can see space between the wall and the chair" or "I can see that there is a space between the wall and the chair." But – as before – we must treat such locutions very carefully. If you could really (or genuinely or authentically) see space, then you ought to be able to answer the question, "What color is that space?" Immediately, you are brought up short. What color is the space between the chair and the wall? If you try to answer that it is colorless, then you might rightly be asked how you could possibly see something which is colorless. In more familiar cases where we use the term "colorless", we can talk of seeing the colorless item, a liter of distilled water for example, because the object refracts light (other objects look distorted in various ways when viewed through the {page 169} object) or because the colorless object exhibits reflections on its surface. But space is supposed to be even more colorless than the most perfectly distilled water. Locally, in our living rooms and on the street in front of our homes, space does not refract the images of objects and space does not boast a surface which sports reflections. Space is thought to be non-refractive and non-reflective. If so, then it must be perfectly invisible. What 'seeing space' amounts to, then, is looking at the places between visible things and failing to see anything there. 'Seeing space' is not the successful seeing of something which exists, but is instead the looking at a place and the failure to see anything there. We do not see space; what we see – and describe in a slightly misleading way – are places devoid of things. This leaves the other case which I mentioned a moment ago. Can't we see space when we look up at the sky on a moonless night? Can't we see the inky blackness of space itself? "Space is not colorless after all; phenomenologically space is black, and can be seen," our critic might object. Often, persons who hold to the theory that space is a kind of thing are not consciously aware that they hold two inconsistent views about space: both that space in our living rooms is colorless and space between galaxies is black. But they cannot have it both ways. And they must be challenged: "Well, which is it, colorless or black, and why the difference?" The simple answer is that it is neither. The tension between the conflicting answers arises out of a misbegotten concept of space. The places between objects, where there are no other objects, are not 'things' of which one can ask, "Are they colored or colorless?" Empty places are not things: they are neither colored nor colorless; they are not black, and they are not any other color either. "Why, then, is the space between the chair and the table, unlike the space between Mars and Venus, not black?" This way of putting the question persists with the confusion. The 'space' between Mars and Venus is not black. We do not see blackness between the chair and the table, not because the space 'there' is some other color, but because we can see, by looking through that place, the illuminated wall beyond. If space existed and were colored, then I could not see my hand when held up a few inches from my nose: the intervening space would block my view. The sky is black between Mars and Venus, not because (interplanetary) 'space' is black, but rather because there is nothing to be seen there (between the planets) and nothing (except for {page 170} an occasional distant star) to be seen further on, either.15
When we look up at the sky on a moonless night and get an impression of black, we are not seeing a black 'thing'. We are not seeing anything at all, and our nervous system fools us, by presenting it to our consciousness as if it were a gigantic piece of coal. Sometimes we get an impression of black from genuinely black physical objects, e.g. lumps of coal and the like. But our nervous system presents (much) the same visual impression when there is nothing there whatsoever. We must take care not to think that if there is a visual impression of black, then there is something there which is black. The ancients used to think that the (night) sky was the interior of a hollow black globe and the stars were tiny holes in that globe through which light shone. We should not want to replace that defective notion with one which would substitute for the black globe an infinite, tenuous, subtle 'container', either black or colorless. Physical things exist, {page 171} and because there are physical things, and only because there are physical things, there are also places. There is no need to posit an antecedently and independently existing physical space, a container, as it were, in which to imbed these physical objects. Neither physics nor our logic requires such a posit. Indeed, the very idea itself is, ultimately, internally incoherent. 8.4 Interlude: The expression "x does not exist" Doubtless one of the things which bemuses, indeed even baffles, persons new to philosophy is metaphysicians' proclivity to pronounce of all sorts of things which non-philosophers regard as relatively familiar that they are, in the end, nonexistent. Metaphysicians have often been known to deny the very existence of such (seemingly) obvious things as space, time, minds, material objects, superegos, evil, miracles, causes, physical laws, free will, and objective truth. Sometimes their negative pronouncements have the result of inducing great curiosity in their hearers, but sometimes the effect is entirely opposite to that intended, inducing, instead, great impatience, even outright alienation. The audience for such claims may find themselves initially protesting: "But surely that cannot be right. It is patently obvious that such a thing really does exist." Such persons may come to regard metaphysics as the wholesale rejection of common sense. Generally metaphysicians know very well that in denying the existence of certain things we are bucking common sense. Metaphysicians are not a species apart. Virtually all of us grow up among the very persons to whom we direct our writings and speak (more or less) the same language as the proverbial 'man in the street'. What explains our talk about "x does not really exist" is our indulging in a kind of literary license, a minor – but possibly potentially misleading – piece of professional hyperbole. Usually such locutions are meant as attention-getters, as a means of highlighting dramatically and forcefully the focus of our concerns. In most cases (but certainly not quite all), the metaphysician who writes "x does not exist" may be found to be advancing a rather more complicated theory, viz. "x does not exist, if by 'x' one means 'y'; and while y does not exist, something else, viz. z does; and taking the latter to be what is denoted by 'x' is a better theory." Put less formally, generally what is involved in the metaphysician's denying that x exists is really the offering of an alternative theory, to be substituted in place of the prevailing, and allegedly defective, theory about the nature of x. {page 172} In denying, as I have just done in the previous section, that space exists, I did not stop simply with making that denial. What was involved in denying that space exists was the elaboration that what was being challenged was a particular concept of space, a concept which would portray space as being itself something like a spatial object. And it is that particular concept, I argued, which is incoherent and in need of replacement. What was not being challenged, indeed what was being insisted upon, is most of what occurs in the ordinary concept, e.g. that there are physical objects, that they are strewn about the universe in different places at varying, and indeed measurable, distances, and that physics can tell us a very great deal about how material objects can interact gravitationally and can tell us the geometry of the path of radiation in the vicinity of massive bodies. In denying that space exists, not only was none of this latter denied, it was positively insisted upon. The claim that space does not exist is my (and several other philosophers') way of calling attention to the fact that space conceived after the fashion of a quasi-physical object is an untenable notion. And thus it goes. Typically when metaphysicians deny that something exists, we do not just leave it at that. What we are in fact doing is offering an alternative theory; we are trying to show that there is something defective in the ordinary notion and are offering a repair. Only rarely, if ever, do we suggest that a concept should be discarded without being replaced by anything at all. In the following section, we will, for the first and only time in this book, encounter a theory, McTaggart's theory of time, which is of the latter sort. McTaggart argued that neither of the two principal theories of time is tenable, and that time does not exist. Few other metaphysicians are disposed to accept his arguments. 8.5 Positive and negative theories of time Just as there are two major theories of space – the 'container' theory and the relational (or Leibnizian) theory – there are two major theories of time. Indeed, I regard it as one of the most important successes of modern metaphysics to have discovered just how much similarity there is, in their formal aspects, between space and time. (We will devote sections 8.7 through 8.10 to the topic of spatial and temporal analogies.) There is a certain problem in what we are to call each of these theories. The first is sometimes called the "absolute", "dynamic", "Augustinian", {page 173} or, simply, the "A-theory". The latter name, "A-theory", does not stand either for "absolute" or for "Augustinian", but derives from J.M.E. McTaggart (1866-1925), who distinguished two sets of temporal terms, one he designated the "A-series" and the other, the "B-series". The second, opposing, theory is sometimes known as the "relative", "static", or "B-theory" of time. In its way, the Augustinian theory of time is the temporal analog of the 'container theory' of space and, not surprisingly, it prompted in Augustine himself much the same sort of bewilderment that we have already seen in Buber: "Time If the future and past do exist, I want to know what they are. I may not yet be capable of such knowledge, but at least I know that wherever they are, they are not there as future or past, but as present. For if, wherever they are, they are future, they do not yet exist; if past, they no longer exist. So wherever they are and whatever they are, it is only by being present that they are. (§18)What Augustine is finally driven to, we see, is a 'psychological' theory of time: the past and the future exist (mysteriously) 'in the mind', but not in objective reality. Any such theory must immediately face the problem how it is possible to measure time. This would be an {page 174} especially acute problem in modern physics where it is commonplace, using exquisitely crafted instruments, to resolve time intervals into million-millionths of seconds. Such remarkable precision seems orders of magnitude beyond what any of us is capable of by psychological reckoning. But even in the far cruder physics of the fourth century AD, a psychological theory of time faced a hopeless uphill battle. Augustine's claim – "It is in my own mind, then, that I measure time. I must not allow my mind to insist that time is something objective" (§27) – is a virtual non-starter when it comes to explaining several persons' common measurements of time. Augustine would have us believe that memories and expectations are the actual objects of our temporal measurements: " How can we summarize the core of Augustine's theory? Augustine, himself, provides a useful characterization: "[Time] can only be coming from the future, passing through the present, and going into the past. In other words, it is coming out of what does not yet exist, passing through what has no duration, and moving into what no longer exists" (§21). You can see here why Augustine's theory has sometimes been called the "dynamic" theory. He posits, not things or events evolving through time, but time itself as moving from the future, through the present, to the past. And you can also see why one might regard such a theory as the temporal analog of the spatial theory which regards space as a 'container'. For just as the absolute theory of space treats space itself (as we have seen) as a quasi-spatial thing, Augustine's theory of time treats time itself as a quasi-temporal thing, i.e. as a sort of thing which "passes" and "moves". And you can see, too, why Augustine's is sometimes regarded as a 'positive' theory of time: because it asserts that there is more to time than just events standing in temporal relations. It may be contrasted with so-called 'negative' theories which assert that there is nothing more to time than events standing in temporal relationships. {page 175} Augustine, to be sure, is not wholly happy with his own theory, and seems constantly to be troubling himself with peculiar questions – ones which arise naturally for a positive theory – such as "While we are measuring it, where is it coming from, what is it passing through, and where is it going?" (§21). But where Buber was driven to despair, Augustine – cleric that he was – was driven to prayer. Throughout his chapter on time, Augustine beseeches God for divine illumination on these mysteries. At the beginning of the twentieth century, McTaggart may be found to be promoting arguments virtually identical to Augustine's. But where Augustine confessed his bewilderment at the results of his own researches and seemed distressed by them, McTaggart unabashedly concludes that time is, in his words, "unreal". It may seem strange that I will take McTaggart to task for this latter conclusion. After all, have I not just finished a moment ago, in this very chapter, a lengthy argument to the effect that space is nonexistent? Why should I be sanguine about my own denial that space exists, and then take exception to McTaggart's claim that time does not exist? There is an important distinction between the sort of theory about space which I have just advanced and the sort of theory about time which McTaggart advances. In denying that space exists, I tried to explain that what that short proposition was to be understood to be asserting was that there is nothing in Nature like what is described by the theory of absolute space. I was denying one particular theory of space, only to be offering what I take to be a better theory, that of relative space, in its stead. And what makes the foregoing enterprise so different from McTaggart's theory of time is that McTaggart, in arguing for the unreality of time, is not offering a theory of relative time to replace or supersede a theory of absolute time, but is arguing against the viability of either theory. McTaggart is not saying, "Time does not exist, if you mean by 'time' y"; he is saying, "Time does not exist, period."16
McTaggart begins by directing attention to two different ways we {page 176} commonly refer to positions in time. Right at the outset, he qualifies his introduction to this topic by writing "as time appears to us prima facie". He can hardly begin by saying that time is one way or another, for he is setting out to prove that time does not exist. Hence he talks of the "appearance" of time, so as not to admit that time does in fact exist: "Positions in time, as time appears to us prima facie, are distinguished in two ways. Each position is Earlier than some and Later than some of the other positions.
The latter of these series, McTaggart calls the "A-series", the former, the "B-series": "For the sake of brevity I shall give the name of the A series to that series of positions which runs from the far past through the near past to the present, and then from the present through the near future to the far future, or conversely. The series of positions which runs from earlier to later, or conversely, I shall call the B series" ([130], §306). McTaggart then proceeds to argue that it is the A-series which is metaphysically more fundamental, for it is the A-series alone which can account for change, not the B-series. The B-series is, in a certain sense, static: it cannot account for an event's changing from having been future, to becoming present, and, finally, becoming past. Take any event – the death of Queen Anne, for example – and consider what changes can take place in its characteristics. That it is a death, that it is the death of Anne Stuart, that it has such causes, that it has such effects – every characteristic of this sort {page 177} never changes.Notice how McTaggart's account of time is reminiscent of Augustine's: the future 'changes' into the present, and the present 'changes' into the past. Once an event is past, then it 'recedes' further and further from the present. According to this account, it is time itself, or positions in time, which undergo change. Various critics have strenuously objected to this account, since it seems to temporalize time itself. Time itself seems to be moving through time: the future 'becomes' the present, and the present 'becomes' the past. The picture seems to presuppose a kind of super-time, against which the flow of 'ordinary' time might be measured. Needless to say, many philosophers have attempted to create theories of time in which such an awkward, and probably unintelligible, notion is not introduced at all. In chapter 11, we will examine a totally different sort of theory, one in which time itself does not change, but it is objects, or things, which change in time. (McTaggart, in §315, explicitly rejects this alternative theory.) But this is to get ahead of ourselves. For the moment, we must see what McTaggart concludes from his argument that the A-series is metaphysically more fundamental than the B-series. He continues by arguing that time itself can exist only if there is something in reality which has the properties of the A-series. That is, he argues that time is real only if there are events which are future, become present, and recede into the past. But there can be no such events. For nothing whatever can have these properties since they are, as he attempts to show, logically inconsistent with one another, and no real (existent) thing can have logically inconsistent properties. Just as a five-sided square would have logically inconsistent properties and {page 178} hence could not possibly exist, McTaggart tries to demonstrate that a time which was future, became present, and receded into the past would have logically inconsistent properties and hence could not possibly exist: Past, present and future are incompatible determinations. Every event must be one or the other, but no event can be more than one.In short, every event has incompatible determinations: it is past, present, and future. The case is analogous to a figure having exactly four and having exactly five sides. The characteristics are incompatible, and no such figure could possibly exist. McTaggart anticipates the obvious objection that he has neglected the tenses of the various verbs. It may seem that this [claim that there is an incompatibility of determinations] can easily be explained [i.e. exposed to be an error]. Indeed, it has been impossible to state the difficulty without almost giving the explanation, since our language has verb-forms for the past, present and future, but no form that is common to all three. It is never true, the answer will run, that M is present, past and future. It is present, will be past, and has been future. Or it is past, and has been future and present, or again is future, and will be present and past. The characteristics are only incompatible when they are simultaneous, and there is no contradiction to this in the fact that each term has all of them successively. ([130], §330)But McTaggart has raised this objection only, in turn, to dispute it. His ensuing counterobjection, i.e. his defense of his theory, lies in his asserting that every moment of time "is both past, present, and future" ([130], §331). As I reconstruct his rebuttal (§331), it seems to me to be something of the following sort. Consider the present moment: it is of course present; but equally, if we were to pick a past {page 179} moment, then the present moment is future; and equally, if we were to pick a future moment, then the present moment is past. Thus, the present moment is not only present, but past and future as well. This reply in defense of his theory strikes me as wrongheaded in the extreme. It strikes me as analogous to, and as unacceptable as, the following argument (where Carol plays the role of Future, Betty of Present, and Alice of Past). Carol is taller than Betty, who in turn is taller than Alice. Focus your attention on Betty. Now, pick someone who is shorter than Betty, e.g. Alice. Compared to Alice, Betty is tall. Now pick someone who is taller than Betty, e.g. Carol. Compared to Carol, Betty is short. Betty is thus both short and tall. But being short and being tall are incompatible determinations. Thus Betty could not possibly exist.I suggest that McTaggart has made the equivalent error. That any moment of time may be present, and equally may – relative to some other moments of time – be future, and equally may – relative to still other moments of time – be past, does nothing to show that any moment of time is both past, present, and future. No more than does your being taller than some persons and shorter than still others establish that you are both tall and short. One need not, then, conclude – as did McTaggart – that time is self-contradictory, and hence, that its very existence is logically impossible. McTaggart's theory of time, which virtually all commentators have subsequently found curious, unorthodox, and – in the end – quite unacceptable, was not just an isolated or insignificant fragment of his philosophizing. It stemmed in large measure from his inability to shake off the Augustinian concept of time, in which time was conceived as something 'moving' from the future, through the present, and into the past. McTaggart marked the culmination, if not quite the end, of a long era of conceiving of time in this familiar, even though confused, manner. The modern approach is, in a way, the very antithesis of McTaggart's. McTaggart's theory, like Augustine's, was a positive theory: it argued that there was something more to time than merely events standing in temporal relations. (Other writers have called this additional feature 'becoming', and argued that becoming could not be accounted for within a negative theory, e.g. within a bare B-series.) Negative theorists propose, in contrast, that temporal relations can be {page 180} treated analogously to spatial relations and that adequate theories of time can be constructed by regarding time as nothing over and above the temporal relations events have to one another. What is currently regarded as being needed, both for metaphysics and for science, is a theory of time which is free of internal inconsistency and which is able to accommodate a variety of facts: (1) that temporal events form a series, i.e. that events may be earlier than, simultaneous with, or later than other events; (2) that there is a present, a future, and a past; (3) that things change, evolve, grow, degenerate, etc.; and (4) that temporal relations – as attested to by the fact that they can be measured by scientific instruments with accuracies far beyond what are psychologically possible – are not 'just in the mind', but are objective facts of Nature. 8.6 The generalized concept of space Descartes and a number of subsequent philosophers, e.g. Locke, have argued that it is of the essence of material objects to be extended in space, i.e. to 'take up room' as we might say more colloquially. Descartes wrote: " Being extended in three dimensions is not, however, a sufficient condition for being a physical object. It is merely a necessary condition. Reflections in mirrors are three dimensional; so are well-crafted projected holographic images. And yet neither reflections in mirrors nor projected holographic images are material objects. Clearly something more, besides being extended in three spatial dimensions, is required for something to count as being a bona fide material object. What is the difference between – let us use as our example – a real (physical or material) chair and its reflection, both of which are extended in three dimensions? The crucial difference is that although the real chair and its reflection in a mirror are both visible, only the former is tangible. Put another way, we can say that although both the {page 181} real chair and its reflection exist in visual space, only the real chair, not its reflection, exists in tactile space. There are in this example two conceptually distinct spaces: that of sight and that of touch. There are, to be sure, remarkable correlations between the two, but the two spaces remain, nonetheless, conceptually distinct. Indeed each and every sensory mode may be regarded as giving us access to a 'space': there is the space of sight; of touch; of hearing; of temperature; etc.18
Whatever correlations there are in the data across sensory spaces (visual-auditory; visual-tactile; etc.) are both contingent and knowable only by experience (i.e. knowable only a posteriori*). As infants we had to learn by trial and error the connection between the visual and the tactile.19 We had to learn that if something felt a certain way, then it would (probably) look a certain way, and that if something looked a certain way, then it would (probably) feel a certain way. Persons born blind who, by surgery, have acquired sight as adults find that it takes them some months before they are able, using their eyes, to recognize objects which are perfectly familiar to their hands.20 As adults, they have had to learn over a period of months, as the rest of us did as {page 182} infants, how to map the data of the visual and the tactile sensory modes back and forth.
In talking and writing uncritically of space, we habitually overlook the differences between visual space and tactile space. But occasional exceptions remind us that there really is not just a theoretical difference between these two spaces, but a real one. Persons born blind have no experience of the features of visual space. But they can detect the features of tactile space. They can tell, by feeling physical things, what their shapes are, how large they are, whether they are rough or smooth, hard or soft, and where they are positioned in relation to other physical objects.21 For the sighted, shadows and holographic images occur in visual space but not in tactile space. And for all of us – sighted and sightless alike – there is at least the logical possibility, as is so often featured in fiction, of invisible objects: things which are detectable tactilely but not visually.
Nonetheless, in spite of the real differences between visual and tactile space, there is – for the normally sighted among us – such a good mapping between the contents of these two spaces that we tend naively to regard these two spaces as one, real, unified, objective public space. We operate with the assumption that if something appears in visual space, then it occurs in tactile space as well, and conversely. But it must be understood that this assumption of a single, unified space of sight and touch, handy as it is, is warranted by contingent facts about this particular possible world. It is not especially difficult to imagine how those facts could be otherwise. With a little ingenuity, we can invent possible-worlds tales in which the enormously useful correlation we find between the visual and tactile in this world simply does not exist. We can describe possible worlds in which your visual data bear little if any detectable correlation with the data furnished by your tactile senses. We can imagine a world, for example, where your hands inform you that you are feeling a teakettle in the cupboard beside the stove, but where your eyes, at that very moment, tell you that you are looking at a distant catamaran hauled up onto the sand of {page 183} a windswept beach. Such a tale is merely an extension of the sorts of stories which are actually true of our visual and auditory senses. I am now looking through an open window and can see rain falling outside. At the same time, I am also hearing Beethoven's Archduke Trio (there is a recording playing in the adjoining room). I – like you – have no difficulty living simultaneously in the two, often disparate, sensory spaces of sight and sound. The correlation between the two is often exceedingly poor. And from such an example, we can see how it could be (i.e. how it is logically possible) that the correlation between the visual and the tactile might be equally poor. The things we standardly regard as being material objects typically exist in (at least) two sensory spaces: the visual and the tactile. Is one of these two spaces more fundamental in our attributing materiality to a thing? Would we be inclined to attribute materiality to something which was visible but not (even in principle) tangible? Would we be inclined to attribute materiality to something tangible but which was invisible? I think the answer is fairly clear. 'Merely visible' things, e.g. shadows, reflections in mirrors, projected holographic images, are standardly regarded as nonphysical.22 In contrast, were we to find a region of space where our hands, sonar, etc. told us there was an object, but where our eyes were unable to detect anything, we would come, especially if the same results were obtained by other persons as well, to regard that place as being occupied by an invisible physical object.
Granted, I may be misjudging the pre-analytic inclinations of other persons. I am, to be sure, depending heavily on assessments of how I actually use the concept of material object in typical cases and of how I would use that concept in unusual cases. I am assuming, as a speaker and writer of a commonly shared language and of a more-or-less commonly shared conceptual scheme, that my own use is fairly typical and that my own leanings in this matter are reasonably representative of {page 184} those of most other persons. Suppose, for the sake of argument, that I have diagnosed correctly both my own and other persons' weighting of the various criteria for invoking the concept of material object: that most of us, if it came to having to choose between the tactile and the visual as being more fundamental to the concept of materiality, would choose the former. If this is in fact true, might there be any explanation for it? Or, is it purely arbitrary which way we choose? I think it is not. I think there is a profound reason why we regard the tactile as the more fundamental. And this reason has to do, once again, with the particular way this world is constructed. In some other possible worlds, the conscious creatures therein might, given the way their worlds are constructed, have good reason to regard the visual as more fundamental than the tactile. I have in mind such facts as the following. Visual buses speeding toward oneself, e.g. images on movie screens, do not (with rare exception, viz. for the fainthearted) injure or kill us; tactile buses do maim and kill. If you lived in a world whose visual images were like those of this world, and whose tactile images were like those of this world, but whose visual and tactile images bore no correlation one to another, then you would quickly have to learn to act in accord with the tactile data if you were to survive in that world and to disregard, save for its entertainment value, the visual data. In this world, tactile knives cut our flesh and cause pain; visual knives do not. Tactile water slakes our thirst; visual water does not. Tactile heaters warm our homes; visual ones do not. All of the immediately foregoing data are contingent. The reported facts, e.g. about the respective dangers of visual and of tactile buses, hold for this particular possible world (and for some others), but not for all. We can imagine possible worlds where precisely the opposite would hold true: where visual buses, but not tactile ones, could kill; where visual water slaked thirst, but not tactile water; etc. In these latter worlds, you would be well-advised to ignore what your fingers and hands were telling you and to pay close attention to what your eyes revealed. It is a matter of course to believe uncritically that the data furnished by our eyes and by our fingers must coincide, that there is a single, unified world external to our skins, and that we have access to that unified world through several sensory modes. But to the extent that this is true, it is not true of logical necessity, it is true sheerly as a matter of contingency. The world did not have to be of this remarkably {page 185} convenient sort; it did not have to accommodate itself so handily to our several sensory modes so as to allow shared access by sight, by touch, and (to a lesser degree) by hearing and smell. We can readily describe worlds in which such redundancy is not the order of the day, indeed in which such redundancy does not exist at all. We take so much for granted. We casually and naively assume that our sight and our touch must reveal pretty much the same data about the world. But the truth is that there is no necessity in this happy fact at all. The world could have been vastly different. That it is this way, and not far less congenial, is really quite dumbfounding and wholly without natural explanation.23
It is not only the coincidence of the visual and the tactile which is remarkable in our pre-analytic concept of physical bodies. It seems not to have occurred to Descartes at all that it might be possible for a physical object to have fewer or more spatial dimensions than three. But by the end of the nineteenth century the idea was being actively explored. In 1884, Edwin Abbott (1838-1926) published an entertaining, and at the same time uncommonly ingenious, book Flatland ([1]) describing a possible world in which physical objects are two-dimensional. The theme has been taken up again, and much expanded, in Alexander Dewdney's recent (1984) book, The Planiverse ([56]).24
{page 186} Once one begins to speculate how different from this another world might be, and thus begins to realize the countless number of ways this world might have been less congenial and the countless number of ways it might have been more, the sheer contingency of our world looms as the most baffling, and in principle the most inexplicable, datum in all of Nature. Anyone who minimizes this aspect of metaphysics has depreciated its essence. 8.7 Extension in time In seventeenth-century physics, there was a quaint expression, "punctiform mass" (sometimes "punctual mass"), which derived from the Latin "punctum", for "point". A punctiform mass was, thus, a mass (i.e. a physical body) which existed entirely 'at a single point'; it was, that is, a zero-dimensional body. The notion of a punctiform mass was invented because it provided a convenient means of solving certain, otherwise intractable, problems posed by the then-current state of physics (footnote 10, p. 52). Even so, in spite of its usefulness in computations, physicists who adopted the concept did so reluctantly and hastened to point out that it was to be regarded as nothing more than a convenient fiction. No real body was conceived to exist only at one point: it was, they all insisted, in the very nature of physical bodies to be extended in space. With the hindsight of modern developments, both in physics and in philosophy, we perceive a curious imbalance in such earlier pronouncements. For if it is in the nature of physical bodies to be extended {page 187} in space, then surely it must also be in their nature to be extended in time. An instantaneous object, one that exists solely for an instant of time, i.e. does not endure for any fraction, however small, of a second, is no physical object at all. Even the most ephemeral subatomic particles of modern nuclear physics, particles which might have an entire lifetime of no more than one trillion-trillionth of a second, at least have some finite temporal duration. But truly instantaneous 'things' cannot be regarded as having real existence. If one is going to opt for the theory that it is of the very nature of physical bodies to be extended in space, then by parallel reasoning (or by invoking analogous intuitions) one similarly ought to propose that it is of the very nature of physical bodies to be extended in time.25 There are perhaps many psychological theories why we human beings have tended to regard space as more 'real' than time and to conceive of physical objects necessarily being extended in space but overlooking {page 188} that they are equally necessarily extended in time. Whatever the psychological explanation may be, it is irrelevant for our purposes. It suffices simply to call attention to our historical conceptual lopsidedness about this issue.
Some persons will try to explain the felt difference in our naive attitudes toward space and time in this way: "Look at any physical object you like. The pencil in your hand will do as an example. Its entire spatial extent is given in your perception; you can see the whole spatial extent of the thing. But you cannot similarly see its entire temporal extent. You see only a brief segment of its total extent in time. The entire spatial extent is present at once, but not its temporal extent." As intuitively appealing as such a line of argumentation may be, it is curiously circular. In a way, it presupposes the very thing that needs explaining. What does it mean to say that the entire spatial extent of the pencil is given in your perception? In looking at the pencil today, we certainly do not perceive what spatial extent that pencil may have had yesterday or may come to have tomorrow. The pencil may have been somewhat longer yesterday (it may have been sharpened and hence shortened last night); similarly it may be shorter again tomorrow. In seeing its so-called entire spatial extent we are seeing only what spatial extent it has now. In looking at the pencil now, what we see is one 'snapshot', if you will, in the entire 'lifetime' of that pencil. The entire lifetime is composed of a continuous series of snapshots. If a physical object ever in its lifetime changes in size or shape, then at no moment of observation can we ever see 'the entire spatial extent' of that object. What we in fact see in one episode of observation is but one thin 'slice' of its existence. Some objects, however, are vastly larger than pencils. Some objects are so immense in their spatial extent that we cannot, normally, perceive that expanse in any 'snapshot' view. The Great Wall of China, for example, meanders for a distance of more than 2400 kilometers (a distance equal, roughly, to that between Paris and Moscow). There is no place on the face of the Earth where one can see both the eastern and the western termini of the Wall. And yet visitors to Beijing do often report that they have 'seen the Wall', have walked upon it, and have photographed it. The Great Wall is extravagantly extended in both space and time; and what counts as 'seeing the Wall' is seeing part of its colossal spatial extent and seeing part of its millennial temporal extent. One does not have to have seen the entire 2400-kilometer {page 189} length, nor to have been eyewitness to the unfolding of its thousand-year history, to be entitled to claim having seen the Wall. Physical objects are multidimensional entities. In this world they are extended in three 'spatial' dimensions, i.e. have width, height, and depth. They are also extended along one temporal dimension, i.e. have some definite (finite or perhaps infinite) duration. Moreover, each is positioned somewhere within the space (or along the continuum) of mass, i.e. each physical object has some nonnegative mass. And in addition each is positioned somewhere within the discrete (i.e. quantized) space of electrical charge, i.e. each physical object has an electrical charge which is some integral multiple of a unit charge. Thus, to say, as is often said nowadays, that physical objects are 'four-dimensional' is actually to understate the case. Physical objects have a number of dimensions beyond their spatial and temporal ones. For our purposes, we will not pay much attention to such further dimensions as mass and electrical charge. It is not that these are unimportant. It is simply that they are not of central concern for the purposes of this chapter. Once one has expanded one's horizon so as to conceive of physical objects, not in the seventeenth-century manner as things extended merely in width, height, and depth, but in the modern fashion as things extended in width, height, depth, and time, then some quite remarkable benefits accrue. One particular benefit, which we will explore in the next section, is the startling insight we are given into the profound analogy between space (i.e. the space of width, height, and depth) and time. Many ancient beliefs – such as that it is possible to move about in space but not in time – are exposed as being straightforwardly based on a confusion and are simply mistaken. The second benefit, to be explored in chapter 11, is that we have a means to solve McTaggart's puzzle about change. Or, if you happen to think McTaggart's puzzle is bogus to begin with and not in need of 'solving', then at least we have a means to address seriously the problem of change without having to posit a super-time against which time itself is moving. By conceiving of physical objects as being things extended in time, we have the conceptual equipment needed to explain change, by identifying change not as a movement of time, but as things having different properties at different times. It is things which change their properties in time; not time itself which changes relative to a super-time. {page 190} Let us turn, then, to examine the first of these alleged benefits, the revealing of the nature and extent of the formal similarity between space and time. 8.8 Taylor on spatial and temporal analogies Over the course of your intellectual life, there will be, if you are fortunate, a number of occasions where a particular lecture, article, or book will prove revelatory. You will happen upon an outstanding piece of work which will open your eyes to a new way of seeing the familiar or seeing through the confusing. In my own career, such a piece of philosophy has been Richard Taylor's 1955 paper "Spatial and Temporal Analogies and the Concept of Identity" ([203]). I regard his paper as one of the classics of modern philosophy.26
Taylor undertakes to prove that there are many more formal* similarities between space and time than are usually recognized; he does this by showing that several of the alleged differences between space and time are just that, alleged, not real.27 To argue for these similarities, Taylor begins by pointing out that many temporal concepts have 'counterparts' (or analogs) among spatial concepts, e.g. the temporal concept now has an obvious spatial counterpart, here. So numerous are these pairings, that we can set up a mapping, or lexicon (see p. 191), for 'translating' between temporal concepts and their spatial analogs. The terms "T1", "T2", etc. designate specific moments of time, e.g. 14:31 Eastern Standard Time on 12 August 1948, or the moment when Columbus first set foot on the continent of North America, etc.; while "P1", "P2", etc. designate specific places, e.g. the northeast corner of the Acropolis, or sixty kilometers due east of the geographical center of Ottawa, Ontario.
There is, of course, one striking disanalogy between temporal and spatial terms: although there is but one temporal dimension, there are {page 191}
three spatial ones. To map the temporal "earlier/later", we must choose one of the three spatial candidates: I have chosen "north/south". (We simply ignore in this exercise "east/west" and "up/down"; these latter spatial terms will not be assigned temporal counterparts. And we will ignore, too, that the dimension "north/south" has endpoints [the poles] while "earlier/>later" may not.) A crucial concept in this exercise is that of part. Normally, when we think of the parts of things we think of their spatial parts. If a thing, e.g. the Trans-Canada Highway, stretches across the continent through Canada, then that part which stretches from the border of British Columbia and Alberta to the border of Manitoba and Ontario may be considered a spatial part of the highway. But insofar as physical things are extended both in space and in time (see section 8.7), we may speak of their temporal parts with as much propriety as we do of their spatial parts. If an object endures, let us say from 12 October 1928 to 19 February 1998, then the temporal interval 23 July 1933 through 5 September 1941 may be regarded as a temporal part of the object. Looking at the last item in our lexicon, we can explain readily the concept of an object O 'lasting throughout' a temporal interval T1-T2: at every moment (instant) between T1 and T2, including the two instants T1 and T2 themselves, there exists some temporal part (called a "T-part") of the object O. Similarly, for an object to occupy the (or better "a") region between P1 and P2 means this: at every point along {page 192} some continuous spatial path (there are of course an infinite number of such paths) connecting P1 and P2 there exists some spatial part (S-part) of the object O. (Note that the path need not be a straight line. Boomerangs [at rest] occupy a continuously connected region of space without occupying the region along the straight line connecting their ends.) With the Lexicon in hand, we can proceed to examine several of Taylor's quite remarkable and startling theses. Thesis: Just as an object may be at one place at two different times, an object may at one time be at two different places. This thesis is surprising just because it has been so often denied. Indeed it is virtually axiomatic in many persons' thinking about space and time that one object may be at one place at two different times, but that one object cannot be at one time in two different places. Their argument might be something of this sort: "This pen which I have carried about in the city today, last night sat on my desk here at home. I am now putting it back on my desk precisely where it had been last night. Yesterday it was in a certain place; today it is back in that very same place. At two different times it has occupied the same place. But no one thing can be in two different places at the same time. If the pen is now on the corner of my desk, it cannot also now be five kilometers away, on the floor of the public library." So familiar is this sort of argument, that one wonders how it is even possible to challenge it. But Taylor does so, and does so successfully. The problem with the argument just given is that it omits to mention one exceedingly important fact. It will not do, for the purposes of arguing that one object can be in the same place on two different occasions, to talk about a certain pen last night and about a different pen (however similar) which occupies that place today. It must be one and the same pen. But how is the identity of today's pen with the pen which existed last night to be accounted for? The usual way for the pen which exists today to be reckoned as being the same pen as one which existed last night is for the pen of last night to have remained in existence until the present moment.28 But once that presupposition in the description of the situation is made explicit, then the argument – {page 193} when repaired – proves not what it is usually thought to prove but precisely its contrary. Let us see why.
The standard way in which it is possible for an object O to exist in one place at two different times comes about through that object's existing at all times throughout that temporal interval. Using symbols, we may express the point this way: O is at P1 at T1 O is at P1 at T2 (where T1 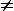 T2) T2)
O exists throughout the temporal interval T1-T2 If this is what is typically involved in an object's being at one place at two different times, then we may state the analogous thesis – for an object's being at one time in two different places – by using the Lexicon to translate all of the temporal terms to spatial terms and all the spatial terms to temporal. The correct, or fully stated, analog thus becomes: O is at T1 at P1 O is at T1 at P2 (where P1  P2) P2)
O exists throughout the spatial interval P1-P2 Is it possible for anything to satisfy these latter conditions? If there is any such thing, then it is a thing which at one time is in two different places. As it turns out, there are countless numbers of actual things satisfying precisely these conditions. There is no need in this instance to take recourse to possible-worlds tales. The actual world provides us untold numbers of examples. The Mississippi River, for example, satisfies the just-stated conditions. At any one time it exists in two different places (e.g. in Memphis and in New Orleans) and exists throughout a spatial interval between those two places (viz. along a path through Vicksburg, Natchez, Baton Rouge, etc.). What is commonly found in cases where an object (e.g. the pen) exists at two different times in the same place is that the object is temporally large enough to span the temporal interval from the one time to the other. In similar fashion, an object (e.g. the Mississippi River or {page 194} the Great Wall of China) can exist at two different places at the same time by being spatially large enough to span the spatial interval from the one place to the other. There is an obvious objection to be anticipated. Someone might protest that in the case of the pen being on the desk last night and being there again today, the entire pen is present on both occasions; but in the case of the Mississippi River's being present in both Memphis and New Orleans, the entire river is not present at either place, only a relatively short stretch of the river's very considerable length is present at either place. But this objection fails to carry through the analogy in its full. What exactly is present, at any given time, when the pen is on the desk? Certainly not the complete temporal extent of the pen, but only a temporal part. What exactly is present, of the Mississippi River, at any given place, e.g. at Memphis or at New Orleans? Not the entire spatial extent of the river, certainly, but only limited spatial parts. It is by identifying "parts" with "spatial parts" and overlooking "temporal parts" that one falls into the mistaken belief that the pen is wholly present at any particular time. But once one recognizes that objects are extended both in space and in time, and that at any one place there exists only a spatial part of an object, and that at any one time there exists only a temporal part of an object, then one can finally understand how objects can be both in one place at two different times and at one time in two different places. An object can be in one place at two different times if it is (temporally) long enough to extend (in time) from the one time to the other; an object can be at one time in two different places if it is (spatially) long enough to extend (in space) from the one place to the other. What, finally, are we to say, then, of the often-proclaimed dictum that it is impossible for one object to be in two places at the same time? Taylor has shown us one way in which an object can be in two places at the same time. My right arm is too short (in its spatial extent) to allow it at any one time to be both in my office and in my living room. (Some three kilometers separates the two places.) But that same right arm is quite long enough to be both on the armrest of my chair and on my desk. As a matter of fact it is in both places now, as I write these very words. This is as far as Taylor's first thesis takes us. But we would do well to linger a moment to ask one more question before moving on to his next thesis. Is the way described in Taylor's first thesis the only way {page 195} for an object to be in two places at the same time? Must every object which is in two places at one time span a path between the two places? It turns out, surprisingly, that there are certain sorts of objects which can occupy two or more places at once without occupying any intervening places. For there are certain things which we count as 'objects' and yet which may be scattered about at a variety of places. Such 'scattered objects' are sometimes called "assemblages" or "collections". The items of clothing which make up my wardrobe, the individual books which make up my personal library, the ships comprising the U.S. Sixth Fleet, are all examples of such 'scattered objects'. Where, exactly, is my wardrobe? Most of it is in my bedroom closet; some of it is on my body; some of it is in my dresser; some is in the laundry room; some is at the dry cleaners; and some is hanging on a hook in my office at the university. My wardrobe is, thus, now at several different places. More exactly, spatial parts of my wardrobe are at several different places. But what makes my wardrobe different from other objects which are also at different places at one and the same time is that the various spatial parts of my wardrobe are not spatially connected one to another; they exist at different places without occupying the intervening places. We often overlook the category of 'scattered objects', believing uncritically that all objects must have spatially connected parts. But there are too many counterexamples to allow us to sustain this naive belief. Where, for example, is Indonesia? or Michigan? or Hawaii? There is no land route through Hawaii connecting Lihue with Hilo. The northernmost island in the chain (where Lihue is located) is unconnected by land to the southernmost island (where Hilo is). (See figure 8.2, p. 196) Yet, if we want to believe that Hawaii is somewhere, i.e. has a place, then we are forced to recognize that some spatial objects (in this example, a large geographical object) do have spatially disconnected parts. And thus not only is it possible for an object to be at different places at the same time, some quite familiar objects are at different places at the same time; moreover, some of these latter objects (e.g. your wardrobe, the state of Hawaii) have spatial parts which are disconnected from one another. Thesis: Time need not be regarded as essential to change. Things may change in space just as well as in time. If by "change" we stipulate that we mean temporal processes, then this claim is legislated to be false by definition. But should we be hasty to make the stipulation? {page 196} 
What does it mean for some object to change in time? There are at least two things that might be meant: (1) that the object changes its place, or (2) that the object changes its properties. If being at different places at different times counts as a 'change in time', then the spatial analog is trivially satisfiable. Using the Lexicon, the analogy becomes, 'being at different times at different places'. But this latter is precisely the identical condition, simply restated equivalently. In short, change of place through time just is change of time from place to place. Things which move about in time from place to place also move about in space from one time to another. Movement in place through time is as much movement in time as it is movement in space. What about 'change in properties' through time? An iron object may start out in a glistening, polished state at T1. But over time, without changing its place, it may gradually rust, so that at T2 it is considerably rusted. Is there a spatial analog? Can an object change its properties through space, i.e. at one time have different properties in different places? It is easy to describe such cases. One end of an iron object, at P1, may be in a glistening, polished state. But at the very same time, along the spatial extent of the object, there is more and more rust. At its other end, at P2, it is considerably rusted. The degree of rust progresses, not through time, but through space. This certainly presents itself as a change, only a change in space, not in time. {page 197} From a formal point of view, objects can 'change' as easily in space as they can in time. There seems to be no good reason to restrict the concept of change solely to change in time. Thesis: In just the way in which it is possible for things to change their spatial positions and relations, it is possible for things to change their temporal positions and relations. Change in spatial position is familiar: an object O1 which had been north of another, O2, may later come to be south of that object. But can an object O1 which had been earlier than O2 come to be later than O2? Taylor argues that the answer is Yes, if we take care to spell out the analogy in full. We begin by stating the conditions for change in spatial positions: O1 at T1 is north of O2Using the Lexicon, we create the temporal analog: O1 at P1 is earlier than O2Is this possible? Can an object (or event) occur before another at some place P1 and after that other at a different place P2? Yes, there are indeed such events. Imagine four persons positioned at equal intervals along a straight line. (See figure 8.3, p. 198.) Alice is at position zero; Betty, one-third of a kilometer further along; Carol, at two-thirds of a kilometer from position zero; and Diane, fully one kilometer beyond position zero. They all have synchronized watches, and at 12 noon, Alice fires a starter's pistol and Diane strikes a drum once. Since sound travels through air at 331 m/sec, just about one second later, at 12:00:01 PM, Betty hears the pistol shot and Carol hears the drumbeat. And one second after that, at 12:00:02 PM, Betty hears the drumbeat and Carol, the pistol shot. Where Betty is standing, the sound of the pistol occurs one second earlier than the sound of the drum. Where Carol is standing, the order is reversed: the sound of the drum occurs one second before the sound of the pistol. A now-familiar objection may be expressed: "When we speak of an object changing its position in space, the entire object is present first at one and then the other location. But in this example, the 'entire' event – the gunshot or the drum stroke – is not present at either place." But, in light of the earlier discussion, the counterobjection {page 198} 
{page 199} should be clear. As objects move about in space, at any given time what is present at a given place is only a temporal-part (T-part) of that object. In the example of the gunshot and the drumbeat, what is required for the analogy to be complete is that at any given place what is present at a given time is only a spatial-part (S-part) of the object. And this latter condition is precisely satisfied. As each of the two 'objects', the gunshot and the drumbeat, spread out through space (at 331 m/sec), spatial-parts occur at given places at given times. The analogy is thus complete. McTaggart, we will recall (see above, p. 176), had explicitly denied that events can change their temporal relations: "If M is ever earlier than N, it is always earlier" ([130], §305). The present example shows that McTaggart's claim is not unconditionally true. McTaggart had overlooked the fact that certain events are of a sort which propagate through space. For such events, their order of occurrence can, and will, vary from place to place. For McTaggart's claim to be made true, it will have to be qualified in this way: "If M is ever earlier at some given place than N, it is always earlier at that place than N." Thesis: To the extent that things can 'tarry' in space, they can as well in time. This thesis has often been denied. Things need not move about in space, it is alleged, but nothing can fail to move forward in time. Everything 'grows older', i.e. moves through time. If, as has often been alleged, things need not move about in space, i.e. can tarry in space, can we construct an analog for something's not moving about in time? For an object to tarry in space means simply that it remains at one place during some temporal interval. Formally, this may be expressed this way: O1 is at P1 throughout the temporal intervalUsing the Lexicon it is easy to construct the spatial analog: O1 is at T1 throughout the spatial intervalRewriting to make the English slightly more idiomatic, we get: At T1, O1 exists throughout the spatial intervalThese latter conditions are trivially simple to satisfy. Any object O1 which, at some particular moment of time T1, extends from place P1 to P2 is occupying a given time throughout some spatial interval. Far from tarrying in time being impossible, it would seem that every physical object which takes up any space whatsoever must satisfy {page 200} these conditions. The spatial analog of 'moving through time' is nothing more, or less, than being extended in space. To 'grow older' is to move through time, i.e. to occupy successive points of time. The spatial analog is simply occupying successive points of space. Thesis: In just the way in which things may move back and forth in space, they may also move back and forth in time. This thesis is the highlight of Taylor's paper. It is the most startling and provocative thesis of the lot. We must begin by attending to the formal conditions for moving forward and backward in space. Obviously, we will have to refer to three different times. We will talk of T1, T2, and T3, where T1 is the first in the series and T3 the last. In English, we can state the conditions this way: "At first, at T1, the object is at place P1, but not at place P2. Sometime later, at T2, the object is at (i.e. has moved to) place P2, and is, of course, no longer (i.e. at T2) at its original place P1. At a still later time, T3, the object has moved back to its original place, P1, and is (of course) no longer at P2." The temporal-counterpart may now be constructed. We will let P1, P2, and P3 be any three ordered positions in space. A bus shuttling back and forth between Vancouver and Burnaby satisfies the former of these two sets of conditions, i.e. it is moving back and forth in space. What is an example of something which satisfies the latter set of conditions? {page 201} To find such an example, we need to look more closely at what it is to move back and forth in space. If we examine the first set of conditions very closely, we see that they satisfy the following, alternative, description: "Consider three ordered moments of time, T1, T2, and T3. If we trace the path through these three points, we discover that at the first time, the object is at P1, at the second time the object is at a different place P2, but when we get to the third and last time, we discover that the object is 'back at' P1 again." Applying the Lexicon to this latter description, we can state the formal conditions for moving back and forth in time in this equivalent, more intuitive fashion: "Consider three ordered points of space, P1, P2, and P3. If we trace the path through these three points, we discover that at the first place, the object is there at T1, at the second place the object is there at a different (later) time T2, but when we get to the third and last place, we discover that the object is there at T1 (i.e. has already been there at the same time it was at P1)." In short, what is required for something's moving back and forth in time is for a thing to be simultaneously at places P1 and P3 and to be at P2 (between those two places) at some other time. Could anything possibly satisfy these conditions? Any
{page 202} 
{page 203} The pivotal point in this last thesis – "In just the way in which things may move back and forth in space, they may also move back and forth in time" – is, of course, in the qualification, "in just the way". For it is not being claimed, for example, that you can now, as an adult, travel backward in time and shake hands with yourself as an eight-year-old, or that you can travel forward to the future and attend your own funeral.30 The claim here is far more modest. It is being claimed only that in the way in which it is possible for (a temporal-part of) an object first to be at one place, (a temporal-part) to be later at another place, and still later (a temporal-part) to be back at the first place, then in a parallel way it is possible for (a spatial-part of) an object at one place to occur at a certain time, (a spatial-part) to be present at a further place at a later time, and (a spatial-part) to be present at a still further place at the same time as (a spatial-part of) it occurred in the first place. If the former of these situations is to count as 'moving about in space', then the latter is entitled to be regarded as 'moving about in time'.
8.9 Is there a temporal analog of the "right / left" problem?31
Immanuel Kant seems to have been the first philosopher to have been intrigued by the differences between what, in modern terminology, {page 204} have come to be called "incongruous counterparts" or – more technically still – "enantiomorphs". Enantiomorphs are mirror images of one another, although not all mirror images are enantiomorphs. The mirror image of the letter "A" is not an enantiomorph; the mirror image of the letter "Z" is. The difference is that there is a (vertical) axis of symmetry in the letter "A", i.e. the letter is symmetrical about its vertical axis: 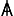 . .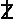 , ,
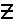 . Hence the letter
"Z"
and its mirror image form a pair of enantiomorphs. . Hence the letter
"Z"
and its mirror image form a pair of enantiomorphs.
Enantiomorphs may be pairs of one-dimensional figures, pairs of two-dimensional figures, or pairs of three-dimensional figures. The one-dimensional figures
are enantiomorphs. Neither one can be moved in a one-dimensional space (i.e. slid sideways) so as to be made to coincide with the other. Of course, if either one were to be rotated in a two-dimensional space, e.g. in the plane of this page on which they are printed, they could be made to coincide. The two-dimensional figures  and and  are
enantiomorphs: neither can be moved about (including being rotated)
in two-dimensional space so as to allow it to coincide with the
other. But while are
enantiomorphs: neither can be moved about (including being rotated)
in two-dimensional space so as to allow it to coincide with the
other. But while  and and  are
enantiomorphs, are
enantiomorphs,  and and  are
not: either one can be moved (rotated) so as to permit it to
coincide with the other. Similarly are
not: either one can be moved (rotated) so as to permit it to
coincide with the other. Similarly  and and
 are non-enantiomorphs, i.e. are congruous
figures. are non-enantiomorphs, i.e. are congruous
figures.
Kant's examples (1783) were of three-dimensional enantiomorphs: " What is there about the right- and the left-handed gloves which accounts for their being enantiomorphs of one another? Each glove we may suppose is made of the same sort of material as its mate, each weighs the same as the other, each has the same total volume as the other, and each has a thumb, followed in order by four fingers: the {page 205} index (or forefinger), the middle, the third, and the so-called little finger. Even so, for all these similarities, there is a profound difference, as all of us who have ever mistakenly tried to fit a left-handed glove on our right hand know very well. Of course we can put labels to these differences: we can say that one of these gloves is "left"-handed and the other "right". But the important question – for Kant and subsequent writers – has been whether or not these terms "right" and "left" could ever be learned by someone who had not experienced the sort of difference exhibited by the pair of gloves. A century later, Kant's problem about the difference between "right" and "left" appears in William James's Principles of Psychology, where it can be seen to be evolving into a problem about communication: "If we take a cube and label one side top, another [presumably the side parallel to it] bottom, a third front and a fourth [again, presumably, the side parallel to the latter] back, then there remains no form of words by which we can describe to another person which of the remaining sides is right and which is left" ([103], vol. II, 150). James's claim, obviously, needs to be qualified. For there is one, trivial, way in which we can describe the difference. We can call the one "right" and the other "left". But we see what James was getting at, even if he managed to express himself poorly. Suppose you are in telephone contact with someone and are trying to get her to duplicate a certain cube whose faces you have labeled in a particular fashion. (See figure 8.5, p. 206.) You want the front labeled with a single dot; the back labeled with two dots; the top, with three; the bottom, with four; the left, with five; and the right, with six. You begin by telling her to pick any side and label it with one dot; to move to the parallel (opposite) side and label it with two dots. Then she can choose any one of the remaining four sides and label it with three dots; and fourthly she is to label with four dots the side parallel to the one bearing the three dots. But now there is a problem (James's problem). In assigning the next two sets of dots, she cannot just arbitrarily pick one of the two remaining sides and label it with five dots, and the sixth, the last, remaining side with the set of six dots: she has to get the fifth choice, the left-hand side, correct. She has to put her five dots on the same side, the left-hand side, as you have put your five dots. You have, that is, to make sure that she is using the terms "left" and "right" in the same way you are, and has not – somehow – got them reversed. (Some persons, we know all too well, frequently mistake the two directions, right and left. Perhaps your telephone correspondent is confused or, even worse, was taught to speak English by {page 206} 
someone with a perverse sense of humor.) How can you make sure that she is using the terms "left" and "right" as you do? You realize that you can solve the problem if you can figure out in which hand she is holding the telephone headset. You ask her, and she replies "my right hand". But still you are not sure that she is using the terms "right" and "left" just as you do. There are various ways you might go about trying to determine whether she is using the words in the same way as you, or in the reverse manner. You might ask her, further, whether she was holding the headset in the hand which is on the same side of her body as her appendix. In this latter instance, you would be assuming that her body was anatomically similar to that of nearly every other woman. Or, again, you might ask her to look up in the night sky and describe, using the terms "right" and "left", the spatial relations of various constellations to one another. So long as you could see those constellations, then you could quickly tell whether she was using the terms "right" and "left" as you do, or whether she had got them 'reversed'. It is clear that there are a variety of ways to tell whether someone, out of sight, with whom you are communicating uses the terms "right" {page 207} and "left" in the same, or a reversed, manner. But all of these ways, it seems, involve presupposing that you and the other person have access to one or more shared enantiomorphs: the asymmetrical disposition of internal organs (e.g. the appendix) in the human body, overhead stellar constellations, etc. The problem is 'cranked up a notch' when these latter, obvious, solutions are explicitly disallowed. Suppose in the Search for Extra-Terrestrial Intelligence (see the discussion of SETI in section 5.2, pp. 80ff.), you are in communication with a distant intelligence, on a planet so shrouded by a dense cloud cover that there is no opportunity for you and her to observe any physical object in common. Moreover, her own body is not at all humanoid. She does not even have an appendix. Of course she does not speak English or any other Earth-based language. You communicate via a code, similar to Morse code, i.e. of pulsating signals. Presuming you could even get to the point of intelligible conversation (again, see section 5.2), could you figure out which term in her language meant "right" and which "left"? Martin Gardner, in his Ambidextrous Universe, states the problem in this manner: Is there any way to communicate the meaning of "left" by a language transmitted in the form of pulsating signals? By the terms of the problem we may say anything we please to our listeners, ask them to perform any experiment whatever, with one proviso: There is to be no asymmetric object or structure that we and they can observe in common. ([75], 160)Gardner calls this the "Ozma problem". (He has borrowed the name from the Ozma project, a 1960 project of SETI, whose director, Frank D. Drake, in turn had borrowed the name from a character in a book by L. Frank Baum.) The Ozma problem has never been raised in regard to any but spatial relations. Is this just lack of imagination? Richard Taylor, we have already seen (section 8.8), has argued persuasively for a very much more thorough analogy between spatial and temporal relations than had previously been thought possible. How much further can we press the analogy? Specifically, can we construct an Ozma problem for time? Is there, that is, a problem with "earlier/later" analogous to "right/left"? The task divides into two stages. First we must formulate the proper analogy, and second we must investigate whether the problem is solvable. {page 208} For current purposes, the Lexicon given above (p. 191) is inadequate. We will require one modification and two additions. Where we had earlier mapped "earlier/later" onto "north/south", we will now map the former onto "left/right". And in order to translate Gardner's statement of the spatial Ozma problem into its temporal equivalent, we will have to have dictionary equivalents for both "pulsating signals" and "asymmetric object". "Pulsating signals" may be taken to mean something like "a series of markers (e.g. audible beeps and their absences) arranged in a temporal order". Implicit in Gardner's story is that the signals or messages should be received during a time, i.e., consecutively, but at one place. A Taylor-analog could, then, be something of this sort: "a series of markers arranged in a spatial order". To ensure the completeness of the analogy we must add the rider that this message should be received within a spatial extent but all at one time. A notched iron bar, for example (where the notches are the coded message), would satisfy the description. The message is extended over a space (i.e. the length of the bar) and is all of it simultaneously present. The temporal analog of a spatially asymmetric object is easy to name but perhaps slightly more difficult to explain. A temporally asymmetric object is one for which there is no moment such that the history of the object up to that moment is the 'reflection' of the future of that object subsequent to that moment. Noticeably the explanation seems to be infected with a slight residue of spatial terminology, viz. "reflection". The term is, however, a mere convenience. We have many more occasions to speak of spatial reflections than of temporal ones, but the suitability of the term for both contexts should be obvious. Most objects are temporally asymmetric, but not quite all. With a little ingenuity we can actually make a temporally symmetric object. For example, a pure pitch of constant volume, physics tells us, would sound exactly the same if recorded and played backward. There is in such an example a temporal axis of symmetry: there is some moment, the midtime of its duration, about which the sound is temporally symmetric, i.e. reflected. It is important to note for our discussion below that physical objects, too, are very often temporally symmetric within selected time intervals. For example, the notched iron bar which we have alluded to may for years undergo no internal physical change whatever. During that segment of its total history it is temporally symmetric. If nothing is happening to it over a course of, let us say, two centuries, then the {page 209} description we give of what happens to it from the first year to the end of the one hundredth year is precisely the same as any description we give of it from the end of the two hundredth year (backward) to the beginning of the one-hundred-and-first year. Putting the matter perhaps a bit cryptically: we cannot tell by examining the bar during that two-hundred-year interval whether it is growing older or younger. In this respect it is the temporal analog of a spatial object which has no preferred direction, e.g. William James's cube. For fairly obvious reasons in the statement of the temporal Ozma problem only temporally symmetric objects are to be mutually accessible to both of the communicators. Allowing a bit of judicious editing, the problem emerges thus: Is there any way to communicate the meaning of "earlier than" by a message transmitted all at once by a series of spatially arranged markers? By the terms of the problem we may send any message we please, with one proviso: There is to be no temporally asymmetric object or structure to which the sender and receiver have mutual access.Does this problem really make sense? Can there be a problem about communicating the meaning of "earlier than" at all analogous to the problem of communicating the meaning of "left of"? We understand how one person communicating with another by telephone should be frustrated in trying to tell the other person, who did not already know, which was her left hand and which her right. Could there really be a problem in trying to instruct the other what the difference between earlier and later is? The very fact that they are communicating at all, that one is saying now this and then that, would seem to solve the problem. Even if, by the terms of the problem, the message must be received in its entirety all at once so that conversation between the two parties over a period of time is explicitly excluded, the reading of the message, unlike the mere receiving of the message, is emphatically not instantaneous but must take some amount of time. We can imagine the sender forwarding the following sort of message: Dear reader: I should like to explain to you how I am using the terms "earlier" and "later". The reading of this message, we both know, takes time. We further know that events are ordered in time. You can understand what I mean by "earlier" and {page 210} "later" by reflecting on the point that as I use the term "earlier" you will have read the word "Dear" earlier than you will have read the word "reader". You will have read "reader" later than you will have read "Dear".This ready solution to the temporal Ozma problem is, however, mere illusion. The argument harbors an important implicit assumption which, when exposed, undermines the conclusion. To reveal this assumption I propose to pursue the problem in a slightly altered, but equivalent, way. Let us imagine the original (spatial) version of the Ozma problem as concerning not the instructing of a remote listener as to which is right and which left, but rather the attempt to discover, by means of the communication link we have described, which items on the distant planet are incongruous counterparts or enantiomorphs of items here on Earth. The two versions of the spatial Ozma problem are equivalent in this respect: a solution to either one would provide a means to solve the other. As we have seen, if we knew that the intelligence with whom we were talking on the telephone had a body spatially congruent to our own, i.e. was not enantiomorphic relative to us, we could simply tell her that her right hand was the one which was on the same side of her body as her appendix. The solution to the first problem provides a means of solving the second, and (it should be obvious) conversely. In the light of this alternative description of the spatial version of the Ozma problem, we can construct a second formulation of the temporal Ozma problem. Under this revision we can conceive of the problem, equivalently, as concerning the attempt to inform the receiver whether the region in which the message originated shares a time direction congruent with that of the receiver or whether the two regions are temporal enantiomorphs of one another. Stating the problem in this way, we can readily see what is wrong with the suggested solution to the temporal Ozma problem: it helps itself gratuitously to one of the two possibilities which are to be decided between. For consider: if the region in which the message is received is suffering a local time reversal, then the test forwarded by our misguided sender will have precisely the opposite effect to the one intended. If we were to observe that strange planet directly it would appear to us to be running backward. Creatures would grow younger instead of older, golf balls would fly out of holes and stop abruptly at the head of a putter, which is then cocked upward, etc. Similarly for {page 211} the reading of the message. Relative to our time, the receiver would "start" reading at what we take to be the end of the message and would finish reading some time later with the word "Dear". "Dear" (contrary to our expectations) would be read later than "reader", not earlier. The analogy with the spatial Ozma problem thus emerges rather more live than the first solution would have led us to think it might. But if this solution does not work, is there any that does? Is there any message conceivable, subject to the constraints given, which would allow the passing of decisive information concerning the relative directions of time in the regions of the sender and of the receiver? The original spatial Ozma problem, the problem of finding out whether our correspondent is like or oppositely handed, is generally acknowledged to be insolvable short of performing certain quite technical (and expensive) experiments in particle physics.32 At the level of ordinary experience, the spatial version of the Ozma problem remains insolvable (see [26]). Is the temporal Ozma problem similarly insolvable? An argument can be given that the latter, temporal, version is also insolvable.
Suppose we were able to observe directly two planets which are temporal enantiomorphs of one another. (If we were to film the histories of both of these planets and then run one film backward, the scenes projected would be indistinguishable.) On one of these planets, the one in which time runs the same way as ours, we see a woman pick up an iron bar, clamp it in a vice, and studiously proceed to file a series of notches in it. For a while filings fall to the floor. At last she is finished, she unclamps the bar, and places it away on a shelf where it sits for a very long time. {page 212} As we look in on the second planet, we see a similarly notched bar sitting on a shelf. At first all appears normal. After a while, however, strange things begin to happen. A woman walks backward into the room, takes the bar from the shelf and clamps it in a vice. A file rises abruptly from the workbench to her waiting hand. She places the edge of the file into one of the notches in the bar. Suddenly some filings leap from the floor to meet the file which is abruptly drawn across the bar, welding these flying particles into the notch in the bar. And so the story goes on. But what about the bars during these longish periods when they sit unchangingly on their shelves? If we look at one of the bars during just that time, we cannot tell on which of the two planets it resides. We must wait to see what happens on that planet. The Ozma problem asks us to imagine such a bar removed from its planet of origin, to imagine it wrenched from its surroundings with their telltale clues and delivered naked to us. Can we tell by examining the bar on which planet it originated? The conclusion we are driven to is that there is no way to tell. Anything that the writer on the first planet could have written could, with equal likelihood, appear verbatim in a message from the second planet. We would be totally unable to assign such a message to one planet or to its temporally reversed counterpart. Thus the analogy between the spatial and temporal versions of the Ozma problem seems complete. Surprisingly, this conclusion too, just like its erstwhile opposite, follows from a defective argument and must be rejected. Let us see why. This latter argument, an argument for the insolvability of the problem, assumes that we can transport the iron bars in question off of each of the two planets described. There is, of course, no problem for the planet in which the direction of time is the same as that of Earth. We can imagine the machinist in the first case returning eventually, taking the bar down from the shelf, ensconcing it in a rocket, and launching the rocket heavenward. Years later the rocket in its aimless flight is intercepted quite accidentally by some earthlings who, knowing nothing of its place of origin, take its cargo home to study. But what story shall we tell for the second case? What sort of causal chain of events can deliver a bar to us from a planet where time is oppositely directed? There would seem to be a profound difficulty in there being communication, or causal interaction, between two planets so related. For the second planet, the rocket-ship account {page 213} simply will not work. For the woman in our second story to take the bar, place it in a rocket, and launch it off into space would for her on that planet be a case of her operating contrary to the laws of thermodynamics. We would expect on this second planet – since time there is running in the reverse direction to our time – that rocket ships would land while sucking in flames and smoke, but not that they should lift off spewing out flames and smoke. How then are we to get possession of the bar? It would appear that the only way for us to receive the described sort of message from a planet whose time direction was opposite to ours would require that there be a violation of some causal laws on one or both of the two planets. So far-reaching is this point that it even requires that we retract the thought experiment which originally set the stage on which the problem was to be played out. We have uncritically imagined someone looking in on both of two planets having opposite time directions. But even this amount of causal interaction is in violation of causal laws. Part of the story we tell of the process of seeing involves the emission of photons from objects and the subsequent impinging of these photons on our retinas. But this process is obviously directed in time. On a planet where time ran oppositely to ours, we could not see objects at all: objects would not be photon-emitters, but would be photon-sinks (i.e. would 'suck in' photons). In sum, the analogy ultimately flounders. The Ozma problem for spatial relations is genuine for all regions of the universe where time is directed as it is on Earth. No causal laws need be violated for two spatially incongruous planets (e.g. where humanoids have their appendixes on the left, rather than the right, sides of their bodies) to be in temporal communication with one another. The analogous situation does not hold for temporally incongruous planets. For two temporally incongruous planets to be in communication by means of a spatially extended message does require the violation of causal laws on one or both of the two planets concerned. Taylor-type analogies between spatial and temporal relations do, apparently, have their limits. The Ozma problem is one feature of spatial relations which is without counterpart among temporal relations. While we can construct an Ozma problem for spatial relations, given things as they stand here and now, we can construct an analogous Ozma problem for temporal relations only if time 'runs backward' in some regions of the universe. {page 214} 8.10 On the connectedness of space and the connectedness of time33
Once again, the problem derives from Kant. In the Critique of Pure Reason, Kant argues that we must conceive of space (i.e. the space of length, width, and depth) and of time as each being unified, i.e. that there cannot be several spaces or more than one time. Kant believes that the human mind is constrained to operate in this manner, that we cannot coherently think of (actually existing) objects which are spatially inaccessible to one another, or of incidents in time which do not stand in unique positions in a single temporal continuum. In effect, Kant's claim about space is that it is a priori necessary for {page 215} any two spatially extended objects to stand in some determinate spatial relations to one another. It is impossible for (the spatial parts of) either object not to be in some spatial direction (south, north-by-northwest, etc.) to (the spatial parts of) the other. Similarly, his claim about time is that it is a priori necessary for any two temporally extended objects to stand in some determinate temporal relations to one another. It is impossible for (the temporal parts of) either object not to be in some temporal relation (i.e. earlier than, simultaneous with, or later than) to (the temporal parts of) the other. All of this is, of course, just another way of saying that space and time are each unified, that the regions of space are not disconnected from one another, and that incidents in time are not disconnected from one another. Like Taylor (see section 8.8), Kant can be seen to be arguing that there is an important analogy between space and time. In this instance, that both can be conceived of only as being unified. Anthony Quinton has challenged Kant's claims about this particular analogy between space and time. Quinton argues ([164]) that Kant is right about time, that time must be unified, but argues that Kant was wrong about space. He argues that space (the space of length, width, and depth) need not be unified. I think that Quinton has made a mistake. I will try to show that Kant was correct in arguing that there is an analogy between space and time in respect of connectedness. That is, I agree with Kant that if either space or time is unified, then so, too, is the other. But where I differ from Kant is in arguing that neither space nor time need be conceived of as unified, that we can conceive of both space and time as being unconnected. In short, Kant was right in arguing that there is an analogy; but he was wrong about what that analogy actually is. Quinton begins by trying to show that space need not be thought to be necessarily connected. (His first argument needs some minor repair, which I will make below; but on the whole it is correct.) Quinton then attempts to construct a parallel argument in an attempt to prove that time need not be thought to be necessarily connected, but finds he is unable to do so. From this, Quinton concludes that Kant was right about time, that time must be unified. I will try to show that Quinton's second argument – for the unity of time – rests on two mistakes, and that his conclusion is not warranted. I will try to show that time, like space, need not be thought to be necessarily connected. Quinton approaches the problem through the now-familiar method of telling a possible-worlds tale. In an attempt to prove that two spatial regions may be totally unconnected to one another, Quinton describes {page 216} a man living in England who when he falls asleep finds himself at a lakeside in a tropical setting. His experiences at the lakeside, unlike many dream-sequences, are as ordinary, as matter-of-fact, and as uneventful as are his everyday English experiences. Nothing dreamlike, fantastic, or wildly unlikely occurs in the tropical environment. The hero passes the day in the tropics and when he falls asleep there immediately finds himself in England. And these English and tropical experiences regularly alternate. Faced with these two sets of experiences both of which are non-dreamlike, both of which seem to be waking experiences, how do we determine which is dream and which is reality? Quinton fills in his tale in such a way as to make the decision arbitrary and hence impossible. To the objection that the lakeside experience is not public, he lets it be public: various other persons in England on going to sleep similarly find themselves in the tropical setting; they meet their English acquaintances there ([164], 142), etc. As the details get filled in, it becomes more and more unreasonable to say of either set of experiences that it is a dream and the other is genuine. Rather, from the contrived similarity of the experiences we would want to say that they are both genuine. They are very unlike dreams: they are not fantastic, they are public, scientific principles work in both, etc. In a word, we would have to say that Quinton's hero inhabits two places. Having effectively argued that it is possible that a person should inhabit two places, the next step of the argument involves determining whether these two places must be located within the same physical space or not. At this point, Quinton's argument falters a bit: "Suppose that I am in a position to institute the most thorough geographical investigations and however protractedly and carefully these are pursued they fail to reveal anywhere on earth like my lake. But could we not then say that it must be on some other planet? We could but it would be gratuitous to do so. There could well be no positive reason whatever, beyond our fondness for the Kantian thesis, for saying that the lake is located somewhere in ordinary physical space and there are, in the circumstances envisaged, good reasons for denying its location there" ([164], 143). To be frank, I do not see what 'good reasons' Quinton has in mind when he says that there are good reasons for denying that the lake is located in ordinary physical space. His assertions to the contrary notwithstanding, as he has described the circumstances, it is perfectly possible that the lake should exist on some other planet in 'ordinary physical space'. Nevertheless his possible-worlds tale can be enhanced in such a way as to yield the results he {page 217} seeks. Rather than simply having his hero 'institute the most thorough geographical investigations' on Earth, let us add to the tale that the hero carries out a thorough exploration of his entire spatial world. Admittedly this is a trifle hard to imagine, but it is not at all logically impossible. At best it is physically* impossible. But since we are telling a possible-worlds tale anyway, a tale which may depart, short of logical inconsistency, as much as we wish from the facts of this world, there is no particular difficulty in adding to the story the information that the hero completes an infinite number of explorations in a finite time. (Perhaps he has a kind of radar-like device whose signal traverses space instantaneously.) In any case, we simply build it into our tale that a complete examination of the space in which either locale is situated fails to reveal the other locale. And with this repair to his tale effected, we can proceed to Quinton's first set of conclusions: the two places are in different spaces, i.e. are spatially unconnected, and Kant's thesis that at most one space is possible is refuted.34
Quinton's possible-worlds tale has one particularly odd feature which he does not comment on, but which, because it may appear to undermine his case, deserves to be made explicit and defended. It is often claimed that a person cannot be in two places at one time. Quinton's {page 218} tale seems to run afoul of this prohibition, for the fellow he describes while asleep in England is simultaneously awake in the tropical setting. He would appear then to be in two places at the same time.35 But while this is true – and undeniably odd in the extreme – it does not, by itself, serve to undermine Quinton's tale. For, as he has described the situation, with there being no causal interaction between the two places, nothing untoward or incoherent follows from the hero's being in two places at the same time. The hero's being in two places at the same time seems to work no mischief in this context and the tale remains innocent. Perhaps the impossibility claim ought to be tidied up to read, "No person can be awake and in two places at the same time", but it is not clear that even this repaired claim is true. In any case we need not pursue it, for – as Quinton first tells the tale – the hero is never awake in two places at the same time. Whenever he is awake in one, he is asleep in the other.
Having constructed his first possible-worlds tale in which he argues for the possibility of there being two distinct spaces, Quinton asks whether we can construct an analogous tale showing the possibility of there being two times. Surprisingly he argues that time, unlike space, is unitary, that there can be only one time. Quinton does not seem to realize, however, that the technique of possible-worlds storytelling is ineffectual for his purposes. Rather than, as in the first tale, trying to establish the logical possibility of a certain proposition (viz., "There are two spatially unconnected places"), he is trying to establish the logical impossibility of a certain proposition (viz., "There are two temporally unconnected events"). It suffices in the first case simply to show that there exists some fairly expansive, consistent description of some possible world or other in {page 219} which the proposition in question ("There are two spatially unconnected places") occurs. But to show, as Quinton wishes, in the second case, that some given proposition is logically impossible, it is insufficient to author one tale in which the proposition ("There are two temporally unconnected events") occurs and to show that that tale is logically inconsistent. Rather, in order to prove the proposition to be logically impossible, Quinton must show that any tale whatever which includes the proposition under survey would be logically inconsistent. The method of possible-worlds storytelling is well-suited for showing that certain propositions (of the form "There is an x such that x is y") are logically possible. All one must do is to find one such story in which the claim occurs and which is free of self-contradiction. But the method is ineffectual when it comes to proving the negation, i.e. when it comes to proving the impossibility of propositions of that form. For now the job becomes, not one of showing that some one story which includes the proposition is free of inconsistency, but rather that every story which includes the proposition is self-inconsistent. What the latter really amounts to is not storytelling at all, but rather explaining why it is impossible to tell a self-consistent possible-worlds tale in which the proposition at issue is included. But this is not what Quinton undertakes. Instead, he proceeds as he did in the first instance. He attempts to tell a possible-worlds tale in which the claim that there are two temporally unconnected events occurs; he argues that this latter story entails a contradiction; and concludes that it is impossible that there should be two temporally unconnected events. Just from considerations of methodology alone we can argue that he has failed to establish his negative thesis. Finding one case in which the supposition that there are two temporally unconnected events leads to an inconsistency does nothing to establish the impossibility of there being temporally unconnected events. His approach to the question can yield only inconclusive results. The method of possible-worlds storytelling cannot establish the negative results he desires. But questions of methodology aside, Quinton commits a second error. There is an internal flaw in the latter possible-worlds tale he tells. Even though, were it successful in entailing an inconsistency, it would still be insufficient to justify his negative thesis, I will try to show that it fails at the more limited task of entailing an inconsistency. For Quinton's latter tale, when shorn of a question-begging assumption, in fact demonstrates precisely what Quinton is trying to deny, viz. that it is logically possible that there should be two temporally {page 220} unconnected events. Quinton produces two arguments ([164], 145 and 146) to show that every lakeside event can be dated in England. I will examine only his first argument. (I think the flaw is virtually identical in both cases.) He asks us to imagine that the fellow who is alternately in England and in the tropics cannot remember whether lakeside events occurred earlier or later than the events he remembers in England. But, says Quinton (switching again into a first-person narrative): "The trouble with this obstacle to unitary dating is that it is too easily circumvented. At the beginning of day 1 in England I write down in order all the lakeside events I can remember. On day 2 in England I cannot remember whether the events of day 1 follow or preceded the lakeside events in the list. But the list will be there to settle the matter and I can, of course, remember when I compiled it" ([164], 145). The error here is subtle. Quinton argues that unitary dating (i.e. the intercalating) of events in the two sequences can be obtained by the simple expedient of daily writing down in one sequence the events one remembers from the other. I agree that this device will work, provided one is writing down one's memories. But how, in a non-question-begging way, is this matter to be decided? How does Quinton's hero know that he is writing down memories (of past events) and not, for example, precognitions (of future events)? Let it be granted that each time the hero of the tale awakes in England he knows one day's worth (or twelve hours' worth or whatever) more information about the lakeside events. I am not calling into question that his writing down of his experiences is the chronicling of genuine occurrences and that he can be said to know that such-and-such events truly are incidents occurring at the lakeside. What I am challenging is his right to describe this knowledge, these daily cognitions in England, as memory. What criteria need be satisfied to entitle us to say of a cognition that it is a case of memory? Are these criteria satisfied or even satisfiable in the case under examination? In order to see what is involved in making the decision between memory and other modes of cognition, let us ask ourselves how we make the decision in the ordinary case, in our normal, ordinary series of wakeful experiences. For convenience' sake, let us for the moment restrict our attention to a single alternative mode of cognition: precognition. Precognition (foreknowledge or prescience), if it occurs at all, occurs so rarely that we need hardly ever trouble ourselves over the matter of distinguishing it from memory. But if it did occur more often and we did have to distinguish it from memory, we could not do so on any intrinsic feature of the experience {page 221} itself or on any introspective basis. No mental phenomena carry with them an identifying mark of memoryhood. Some of the things we think we recall never happened at all, yet introspectively these thoughts (images, beliefs) are indistinguishable from genuine memories. Merely being memorable or, more exactly, having the felt quality of a memory is no guarantee of the truth of that which has that quality. Our mental faculties can be faulty or deceived. We can believe that we remember events and it turns out that these events did not occur, and similarly we can fail to remember events that did occur. That a thought or mental image is really of a past occurrence and not perhaps a precognition of a future one is guaranteed by nothing in the thought or the image itself. The manner in which memories and precognitions present themselves to consciousness seems to be all of a piece. To learn that a memory-like thought is really a memory and not a precognition we must depend ultimately on objective criteria and more exactly on physical criteria. Generally we do not have to depend on physical criteria, for we quickly come to learn by experience that in virtually all cases when we have memory-like experiences we are having genuine memories. But if precognition were a common occurrence we would then have to rely not on this (just mentioned) statistical generalization but on the 'testimony' of singular physical facts. We can understand that, under these latter circumstances, we would have to ask ourselves, "Look, self, I seem to recall writing a contract with Jones. Am I remembering or precognizing?" It would do little good to attempt to secure the corroborative testimony of another person, Jones himself for example, for he would presumably have precisely the same quandary. The answer to the question whether I (or we) are remembering or precognizing is decidable only by looking to see whether the contract exists now. If it does, we are remembering; if it does not, we are precognizing. Ultimately, if the question of deciding between memory and precognition seriously arises for a group of persons all of whom share the same cognition, then it is answerable only by the testimony of physical facts. If we lived in a world where precognizing was as common as remembering, then Quinton's argument would be all-too-obviously question-begging. But even if it is not obviously question-begging, it is question-begging nevertheless. We need only raise the question of the possibility of precognizing as an alternative description of what Quinton's hero is doing, to see that the question is unanswerable in his tale. What right, we should want to know, does Quinton's hero have to {page 222} assume that he is remembering rather than precognizing? The answer: None. In a world where precognizing is an acknowledged possibility, even the corroboration of others who shared similar lakeside experiences would be inadequate to decide between a case of memory and one of precognition. If England and the tropical lakeside were spatially and temporally connected, we could appeal to physical records, to the causally linked remnants of past events – photographs, memoranda, burnt embers, contracts, and the like – to settle whether the 'memories' one has in England of the lakeside were genuine memories or precognitions. If a man could pass through Paradise in a dream, and have a flower presented to himBut Quinton's tale of the two spatially unconnected places is so constructed as to preclude the very possibility of there being physical records shared in the two worlds ([164], 143). There are no physical objects common both to England and to the lakeside environment. There are no clocks, starscapes, written memoranda, or even rocks that occur in both worlds. But what about persons' bodies? Cannot the required records be made on them? Suppose Quinton's hero were to write down on his own skin a diary of events as they occurred in the tropics. Wouldn't the hero then know, when in England, that the events recorded on his skin happened earlier? Since causes always precede their effects, the requisite proof would seem literally to be in hand. This latter repair will not do. For as Quinton tells the tale, his hero does not have one body in two places or even one body now in England and later in the tropics: his hero has (or inhabits) two bodies.36 The English body (we can guess) is a pallid white wracked with chilblains; the tropical body is a sunbathed bronze infused with robust good health. The English body does not become tanned, and the tropical body does not grow pale.
The 'linkage' between the two worlds is experiential, not physical; {page 223} persons reside in both worlds but not physical objects. And the testimony of persons in the absence of corroborating physical evidence is indecisive in the matter of deciding between memory and precognition. Quinton's 'traveler' is not entitled to describe his cognitions in England of his lakeside experiences as being memories. That they merely 'feel like' memories is simply not good enough evidence in the face of a serious challenge to the claim that they are memories. Thus, we must give a different description of the hero's memory-like thoughts. But what description? Having gone to some trouble to expose one question-begging way of telling the possible-worlds tale, we must be especially careful not to fall into the trap of replacing it with another. It would be all too easy to argue that since we are not entitled to say that the hero remembers the lakeside events, we must say instead that he either remembers, simultaneously cognizes, or precognizes those events. In effect, we replace a single description (viz. "remembers") with three seemingly exhaustive possibilities (viz. "remembers or simultaneously cognizes or precognizes"). But to make the claim that these three alternatives exhaust the possibilities is just to presuppose the truth of precisely what is in question, namely, the Kantian hypothesis that all events are temporally related to one another. If we are to avoid prejudicing our tale a second time, we must take care to drive a non-Kantian wedge at this point. We must, at the very least, seriously entertain a fourth possibility, to wit, the possibility that our traveler, upon awakening in England, genuinely cognizes lakeside experiences, but the lakeside experiences themselves are neither earlier than, simultaneous with, nor future to the time of cognizing them in England. To say of something that it is a memory logically guarantees that it is true of a past event. If the hero of Quinton's tale when in England were able to identify his seeming memories as genuine memories, then Quinton's and Kant's claim that all temporal events may be organized into a single temporal sequence would be reinforced. But this is precisely what is impossible in Quinton's own tale. There is no way whatsoever in Quinton's tale for the hero to ascertain what the status is of his seeming memories of the lakeside. There is nothing whatsoever to indicate whether they are memories, simultaneous cognitions, precognitions, or – even more drastically – none of these. In short, contrary to Quinton's own conclusion, the events of the lakeside cannot be intercalated with those of England. It would seem, then, that there is no reason whatever to persist with the Kantian thesis that time must be unitary and that such a property of time is known a priori. {page 224} Space and time may in fact be unified. But if they are, then – contrary to Kant – this is no a priori truth. We are not constrained to think of all regions of space as being connected and all events in time as being connected. This conclusion holds not just for the space and time of physics or natural science. What I have tried to show is that it is possible that the space and time of human experience may have unconnected elements. With some imagination, we can describe possible experiences which, if they were to occur, would warrant our insisting that experiential space and time are not unified. 8.11 Time travel One kind of time travel is so common, so familiar, that it is rarely ever recognized for what it is. All of us – except those at death's door – have an ability to travel forward in time. All we have to do is wait. Waiting is the simplest and most direct form of time travel. Most parents know this intuitively, although perhaps without ever having realized that they do. When youngsters, filled with the anticipation of a birthday party, say impatiently, "I wish it was tomorrow",37 their parents will often counsel them by saying, "Just wait; it will be."
But waiting has two drawbacks. First, it is strictly forward-directed: one can travel into the future by waiting, but not into the past. Moreover, there does not seem to be any analogous 'operation' which will take us backward in time. There is no such thing as 'reverse-waiting' or 'unwaiting'. The second drawback to waiting as a mode of time travel is that it proceeds in lockstep with the ticking of the clock. To get from noon today to noon tomorrow takes twenty-four hours of waiting. What persons who are seeking 'better' methods of moving about in time clearly want is a way of getting from noon today to noon tomorrow without having to spend twenty-four hours in the process. A minute or two of traveling time is far more attractive to them. Taylor has shown us one way of traveling forward and backward in time. Objects which are curved in space can, as we have seen, perform the temporal equivalent of objects moving back and forth in space (see pp. 200-3). But that is of scant use to the person wanting unlimited capacity for time travel. By bending my body into a The concept of moving forward or backward in time by great leaps is intelligible. Suppose it takes me eight hours to digest a meal and suppose that in one day my hair grows 0.06 cm. Now suppose that I am placed into a 'time machine'. I sit in the machine for the time it takes me to digest the meal I just ate. In this same time my hair grows 0.02 cm. In short, my body has aged eight hours. But suppose when I step out of the machine it is one year later than when I stepped into the machine. This would be a case of the sort of time travel which is depicted in countless science-fiction writings. We will call this 'accelerated' time travel. Is accelerated time travel possible? Forward-directed accelerated time travel is certainly logically possible. It may even be physically possible. Indeed the technology may be imminent. If cryogenic freezing (low-temperature 'suspended animation') can be realized for human beings, it would certainly qualify as forward time travel. We already possess the technology to forward accelerate in time certain creatures (e.g. the fish Dallia pectoralis [145], 19), which can be frozen alive and subsequently thawed and revived with little or no permanent damage.38
But the real problem has always been with the notion of backward-directed time travel. Is accelerated backward time travel physically possible? There is a certain amount of empirical evidence that it is not. The best of this evidence is simply the fact that, so far as we can tell, no one has traveled to the here and now from any time or place in the future. Of course such evidence is not conclusive: it may be that future generations will have destroyed themselves in a war or environmental disaster; or it may be that they will have enacted legislation with sufficiently severe sanctions and policing to prevent time travel to our century; etc. Nonetheless, the very fact that there are no visitors here and now from the future strongly suggests that at no time in the future will a means be found to permit traveling backward in time. And the fact that it will never be done in turn suggests that it is physically impossible. But even if backward time travel were to be physically impossible, {page 226} might it still be logically possible? Even if this world is of such a sort that traveling backward in time cannot be realized, might there be other possible worlds where traveling backward in time does occur? Many persons have thought that traveling backward in time is logically impossible. Their arguments typically are of this sort: "If you could travel backward in time, then you could encounter yourself when you were a youngster. Even if you are not normally homicidally inclined, it is at least theoretically possible that you kill that youngster. But if you did, then you would not have grown up to have reached the age when you traveled back in time. Thus there would be a contradiction: you both would and would not have traveled backward in time. Since the story involves a contradiction, it is logically impossible to travel backward in time." Such arguments have been around for years. They are especially tricky because they involve what are called modal* concepts, in particular the notions of possibility and impossibility. Does the very concept of travel into the past entail contradictions? Does the possibility of murdering yourself as a child show that backward-directed time travel is an impossibility? The answer is: there is no possibility, if you travel into the past, of murdering yourself as a child. The very fact that you are here now logically guarantees that no one – neither you nor anyone else – murdered you as a child, for there is no possibility of changing the past. This notion that one cannot change the past needs careful attention. There is nothing special about the past in this particular regard. For you can no more change the past than you can change the present or change the future. And yet this is not fatalism. I am not arguing that our deliberations and actions are futile. I cannot change the future – by anything I have done, am doing, or will do – from what it is going to be. But I can change the future from what it might have been. I may carefully consider the appearance of my garden, and after a bit of thought, mulling over a few alternatives, I decide to cut down the apple tree. By so doing, I change the future from what it might have been. But I do not change it from what it will be. Indeed, by my doing what I do, I – in small measure – contribute to making the future the very way it will be. Similarly, I cannot change the present from the way it is. I can only change the present from the way it might have been, from the way it would have been were I not doing what I am doing right now. And finally, I cannot change the past from the way it was. In the past, I changed it from what it might have been, from what it would have been had I not done what I did. {page 227} We can change the world from what it might have been; but in doing that we contribute to making the world the way it was, is, and will be. We cannot – on pain of logical contradiction – change the world from the way it was, is, and will be. The application of these logical principles for time travel becomes clear. If one travels into the past, then one does not change the past; one does in the past only what in fact happened. If you are alive today, having grown up in the preceding years, then you were not murdered. If, then, you or anyone else travels into the past, then that time traveler simply does not murder you. What does that time traveler do in the past? From our perspective, looking backward in time, that traveler does whatever in fact happened, and that – since you are alive today – does not include murdering you. Time travel into the past involves no intrinsic contradiction. The appearance of contradiction arises only if one illicitly hypothesizes that the time traveler can change the past from what it was. But that sort of contradiction has nothing whatever to do with time travel per se. One would encounter the same sort of contradiction if one were to hypothesize that someone now were to change the present from the way it is or someone in the future were to change the future from the way it will be. All these latter notions are logically impossible. But none of them is intrinsic to the concept of time travel. One should take care in describing time travelers not to give them logically impossible capabilities, e.g. the capacity to change the past from the way it was, the present from the way it is, or the future from the way it will be. But once one has done that, then there is no need to think the concept of time travel to be logically impossible. It just turns out to be a contingent fact about this actual world that accelerated backward travel in time does not occur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 )-shaped.
)-shaped.